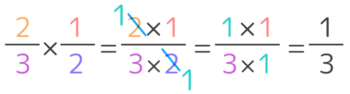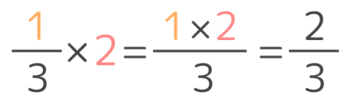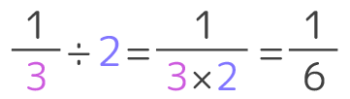「分数が分からない・苦手・嫌い！」という小学生の方は、分数は難しいものと思っているかもしれません。でも実は基本的な事をいくつか覚えれば、あとは簡単に分かるんですよ。
この記事は東大卒講師歴20年の図解講師「そうちゃ」が重要基本事項をまとめました！読み終える頃には分数に対する苦手意識は吹っ飛んでいるでしょう♪
この記事は長文になっているので、下の目次から「分数のかけ算わり算」など読みたいところをクリックしてジャンプして下さいね！
目次(クリックでジャンプ)
分数の基本(小2～3)
爽茶分数の要素と呼び方
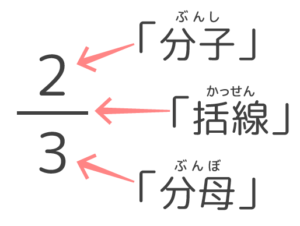
分母から先に読むので、この分数は、「さんぶんのに」と読みます。
分数の意味(二つ)
❶1個のモノを等分したいくつか
(例)23→1個のモノを三等分したうちの二つ
❷分子÷分母 (例)23→2÷3
小学4年生以降の人には2つ目の意味(分子÷分母)が重要です。
「下÷上」でなく「上÷下」であることに注意しましょう。
13を割り算に直しなさい(計算はしなくてもよい)
→( 上(分子)÷下(分母)で1÷3 )
分数の大きさ
❶分子(上)が大きくなると、数量としても大きくなります。
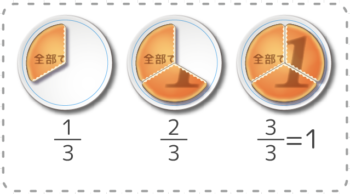
❷一方、分母(下)が大きくなると、数量としては小さくなります(分け方が細かくなるので)。
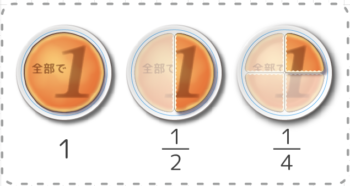
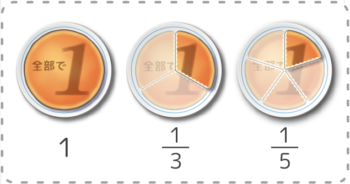
一番大きい分数はどれですか？
①(57、17、37)
→( 分母が同じなので、分子が大きいものを選んで、57 )
②(27、23、211)
→( 分子が同じなので、分子が小さいものを選んで、23 )
小数との関係(数直線)
小数の大きさを考えれば分かりますね。
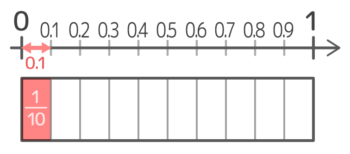
0から1までの長さを十等分したのが110です。
➀0.3を分数にすると？→(0.1が3個分なので、310)
➁0.7を分数にすると？→(0.1が7個分なので、710
)
爽茶分数が表す数量(～小5)
上の絵では全体を1としましたが、今度は具体的な数値にして考えます。
「AのCB」=A÷B×C
(例)12kgの23→12÷3×2=8g
➀1000mの25は何m？→(1000÷5×2=400m)
➁25kmは何m？→(1km=1000m なので、25kmは1000mの25と同じ)→(1000÷5×2=400m)
③56時間は何分？→(1時間=60分なので、60分の56と同じ)→(60÷6×5=50分)
分数の種類(小4)
分数は次のように3つの形(種類)があります。
❶真分数 ❷帯分数 ❸仮分数
23 123 53
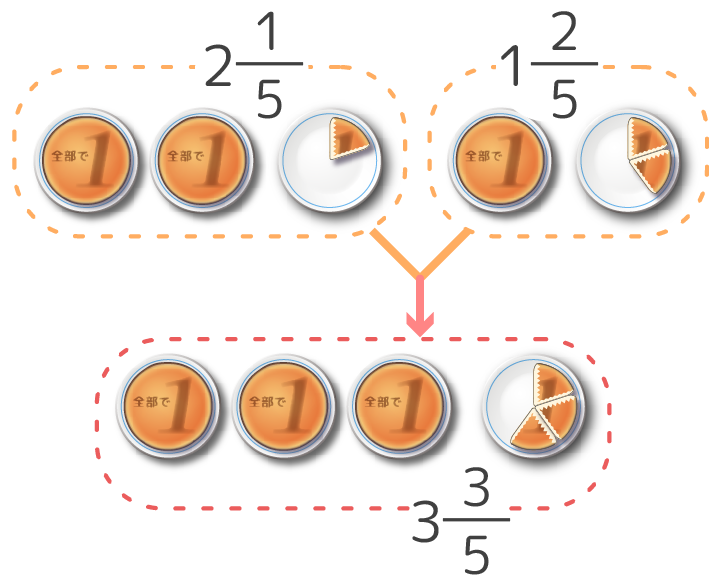
❷帯分数と❸仮分数は同じ大きさを2種類で表したものなので、互いに形を直すことができます。
123⇔53
分母は変わらないのがポイント♪
計算の途中は仮分数、答えを書く時は帯分数と考えると良いです。
帯分数を仮分数に直す
帯分数の整数部分×分母+分子の答えが仮分数の分子になります。分母は変わりません
仮分数に直しなさい。
➀245→(2×5＋4＝14)→(145)
➁327→(3×7+2＝23)→(237)
仮分数を帯分数に直す
仮分数の分子÷分母で余りのある割り算をして、答えが帯分数の整数部分で、余りが分子になります。分母は変わりません。
帯分数に直しなさい。
➀112→(11÷2＝5あまり1)→(512)
➁135→(13÷5＝2あまり3)→(235)
「詳しい説明を見たい」「問題を解きたい」「分数の大小問題を解きたい」という人は「分数の種類と帯分数から仮分数への変換」を見て下さい。
練習をしたい人向けにオススメの問題集を記事の一番下で紹介しています。
分数の操作(小5)
分数は見た目を自由に操作できるのが特徴です。
表す大きさ(数量)は皆同じ
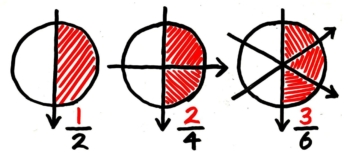
分母と分子に同じ数をかけても(倍分)
同じ数で割っても(約分)
大きさは変わらない
分数の操作は3種類あります
- 約分→分子と分母を同じ数で割る
- 倍分→分子と分母に同じ数をかける
- 通分→2つ以上の分数をそれぞれ倍分して
分母を同じ数にする
約分
分子と分母を同じ数で割れなくなるまで割ります。
例えば3045の場合、こうなります。
既約分数
上の例での23のように、もう約分できなくなった分数を「既約分数」と呼びます。
3042
を約分すると？→(3042-(÷2)→-(÷2)→1521-(÷3)→-(÷3)→57)
倍分
倍分は約分と違って無限にできます。
➀12=(3)6=15(30)
➁1=3(3)=(7)7…(1は分子と分母が同じ分数になる)
「くわしい説明を見たい」「問題を解きたい」という人は「分数の操作方法。約分と倍分(小学5年生)」を見て下さい。
通分
分母が違う分数は足し算引き算ができないので分母をそろえる必要があります。これが通分です。
→分母を(最小公倍数に)そろえる事
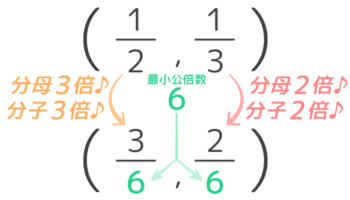
例:12と13を通分
…分母を2と3の最小公倍数6にそろえる
・12→(分母分子を3倍)→36
・13→(分母分子を2倍)→26
最小公倍数を求めたら、分母を見て何倍にするかを考えて、分子も同じだけ倍します。
23と15を通分すると？
→分母を(3と5の最小公倍数15)にそろえると、(23–(分子5倍)→–(分母5倍)→1015と15–(分子3倍)→–(分母3倍)→315)で、答えは(1015,315)
「くわしい説明を見たい」「もっと問題を解きたい」という人は「分数の通分。分母をそろえる(小学5年生)」を、最小公倍数の求め方を復習したい人は「公倍数の意味(書き出しで求める)」か「2つの数のすだれ算」を見て下さい。
練習したい人向けにオススメ問題集を記事の一番下で紹介しています。
主に中学受験で問われる応用問題には以下のものがあります。
・約分と分子と分母の和など
・分数の大小比較
・既約分数の個数
・範囲内の 〃
・分数の分割による計算の工夫
姉妹サイト「そうちゃ式1号館」の「分数の応用問題」を見て下さい
分数と小数・整数(小5)
分数計算や割合計算で、分数と小数・整数を一緒に使うことがあります。頭がゴチャゴチャになる人もいるかもしれません。
コツは、迷ったら分数に統一すること です。
整数→分数
整数は必ず分数で表すことができます。
1を分母につける
(例) 5 → 51
小数→分数
通常の分数
(最後まで書いてある)小数は分数に直すことができます。
●小数第一位までの数→10を分母につけて約分
(例)0.4→410→25
●小数第二位までの数→100を分母につけて約分
(例)0.15→15100→320
●小数第三位までの数→1000を分母につけて約分
(例)0.125→1251000→25200→540→18
確認テストをどうぞ
0.6→(610→35)
0.36→(36100→925)
0.056→(561000→28500→14250→7125)
「くわしい説明を見たい」「もっと問題を解きたい」という人は「分数と整数・小数」を見て下さい。
循環小数
さらに、小数点以下が永遠に続く小数でも、規則的な数の列になる場合(例えば0.333… これを「循環小数」と言います)は工夫することで分数に直せます。
－)⑩=3.333333…
－)➀＝0.333333…
－)⑨=3.000…=3
→ ➀=3÷9=39=13
小数点以下の循環部分を一気に消します
もっと循環小数の問題を解きたい方は「循環小数の問題」を見て下さい
それ以外の小数
円周率3.14…のように、小数点以下が永遠に続いて規則的な数の列にもならない場合は分数に直せません。(「無理数」と言います)
分数→小数・整数
分数の意味は「分子÷分母」なので、分子÷分母の割り算をすれば小数にできます。
(例) 12=1÷2＝0.5
割り切れない場合でも、答えが規則的な数の列になる場合(例えば13=1÷3=0.333…「循環小数」)は繰り返し出てくる部分に特別な記号をつけて「0.3」のように表せます。
分数と小数の大小比較
分数と小数の大小を比べる時は、小数に揃えるのが簡単なことが多いです。
「くわしい説明を見たい」「問題を解きたい」という人は「分数と整数・小数」を見て下さい。
爽茶分数の足し算・引き算
(小3～5)
爽茶丁寧に復習して身につけましょう。
分母が同じ場合(小3・4)
真分数(小3)
分子だけを足し引きする。分母はそのまま
例1：15+25=1+25=35
例2：：35－25=3－25=15
➀37+47は？→(3+47=77=1)
➁1113－813+413は？→(11－8+413=713)
「くわしい説明を見たい」「もっと問題を解きたい」という人は「(小3)分数の加減算➀真分数の足し算引き算」を見て下さい。
帯分数(小4)
帯分数の場合は、横の整数同士を足し算引き算してもOKです。
→整数と分子同士を足し引きする。
分母はそのまま
足し算で分子が大きくなった場合は繰り上げを、引き算で分子の引き算が出来ない場合は繰り下げを行います。
・4117→4+117→4+147→547
・413→3+1+13→3+33+13→343
➀567－327は？→(整数と分子を引いて、247)
➁145+235は？→(375→3+75→3+125→425)
③415－135は？→(415→3+1+15→3+55+15→365としてから、365－135=235)
「くわしい説明を見たい」「問題を解きたい」という人は「(小4)帯分数の足し算引き算」を見て下さい。
分母が違う場合(小5)
通分してから、分子だけを足し引き
12+13＝36＋26=56
確認テストをどうぞ
(作成中)
「くわしい説明を見たい」「問題を解きたい」という人は「(小5)分母が異なる分数の足し算引き算」を見て下さい。
この「通分をする分数の足し算引き算」が、分数の最大のヤマ場です。ここで分数を苦手になる小学生が多いです。
問題集で練習したい人向けに記事の一番下でオススメ問題集を紹介しています。
苦手になりかけた小学生に分数を教える時は「分数の教え方(小学5年生用)」が参考になると思います。
分数のかけ算・わり算
(小5～6)
分数×÷分数(小6)
足し算引き算より、こちらの方が簡単ですね。
❶分子同士・分母同士をかければ良い
❷整数と帯分数は仮分数に直して計算
❸計算途中で約分をしてもよい
❹答えるときは帯分数に直す
わり算は「÷」の直後の分数の上下を逆さま(逆数)にしてから、かけ算。
❶分子分母をひっくり返してわり算をかけ算にする
❷分母と分子をひっくり返した数＝逆数
(例)23の逆数は32
確認テストをどうぞ
23×57=( 2×53×7=1021 )
14÷25=( 1×54×2=58 )
23×225=( 2×123×5=2×41×5=85=135 )
37×1415÷25=( 3×14×57×15×2=11=1 )
「くわしい説明を見たい」「問題を解きたい」という人は「分数と分数のかけ算わり算」を、特に「逆数にする理由が知りたい」という人は同記事内の「逆数をかける理由」を見て下さい。
分数×÷整数
小6以降のやり方
整数は分母に1をつけて「N1」という分数にして計算します。
16×4＝16×41＝1×46×1=1×23×1=13
16÷4＝16÷41＝＝16×14＝＝1×16×4=124
確認テストをどうぞ
310×5=( 310×51=3×510=3×12=32=112 )
415÷7=( 215÷71=215×17=21×15×7=3×15×1=35 )
小5のやり方
小学校では「分数と分数のかけ算割り算」より「分数と整数のかけ算割り算」を先に学習する関係で、1NにせずNのまま計算する方法を習います。
分子と整数をかければ良い
分母に整数をかける
今現在小5の生徒さんとその保護者様は「(小5)分数と整数のかけ算わり算」を見ると良いかもしれません。
小6以上の方はN1に直す方法で大丈夫です。
かけ算わり算の混合計算
÷の直後の分数だけを逆数にして掛け算
13÷12×15=13×21×15
=1 x 2 x 13 x 1 x 5=215
分数の混合計算(小6)
爽茶一度、頭を整理しましょう。
分数計算の区別のポイント
分数計算のルールの「違い」をしっかり意識させます。一番のポイントは「通分のあるなし」です！
●足し算・引き算→通分してから計算
(例)12+13=36+26=36
●かけ算・割り算→通分せずに計算
(例)12×13=1×12×3=16
お子さん・生徒さんに「計算規則をもう一回整理して教え直したい」という人は「分数の教え方(小学6年生)」を見て下さい。
最後に総まとめとして、混合計算を解いてみましょう。これが解ければ分数は大丈夫です。
(作成中)
(作成中)
「もっと問題を解きたい」という人は「分数の混合四則計算」を見て下さい。
分数の応用問題(中学受験)
中学受験で使うような応用問題については、姉妹サイト「そうちゃ式 新1号館」の「分数の応用問題」を見て下さい。
おすすめ教材
爽茶オススメ問題集
●「毎日のドリル」(学研)はスマホアプリとの連携でやる気をアップできる問題集です。(くわしい案内はこちら)。
●「くもん小学ドリル」も定評ある教材でオススメ
●「分数の計算(算数基礎マスター)」は3年から6年の分数計算をカバーしているので学校の予習復習はもちろん、中学受験に向けた先取り学習にも使えます。低学年のうちに買うと長く使えてオトクですよ！
「分かりやすい！」と評判の
今なら14日間無料♪この期間内に利用を停止すれば料金は一切かかりません。この機会に試してみては？