小学6年生】分数と分数のかけ算×のやり方は？分かりやすく教えます♪

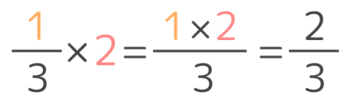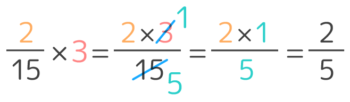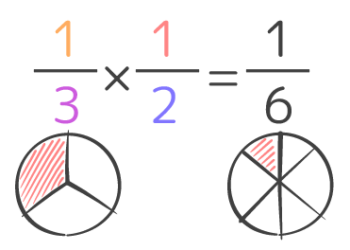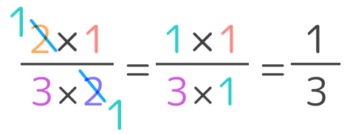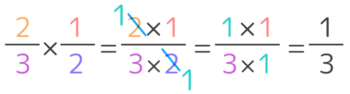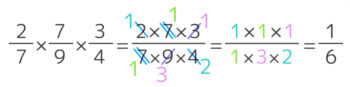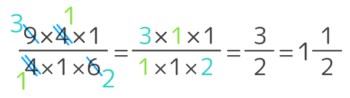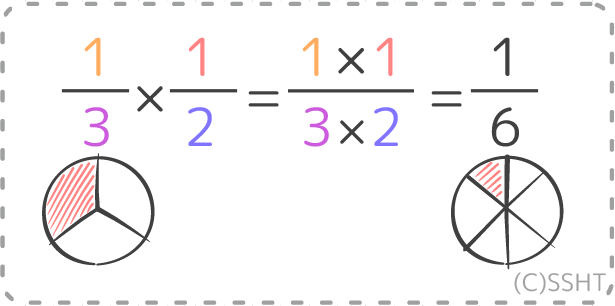
「分数と分数のかけ算のやり方が良くわからない・忘れた」という小学6年生の方、大丈夫ですよ！東大卒講師歴20年の図解講師「そうちゃ」が分かりやすく教えます♪読むだけでスラスラ解けるようになっているでしょう

(復習)分数と整数

小5の三学期に「分数と整数のかけ算」を学習しました。まとめると、こうでしたね！

思い出しましたね？では「分数×分数」を始めます。

分数×分数のやり方を理解

並べて「かける」だけ!

さて質問です。上にあった「分数×整数」の問題で…

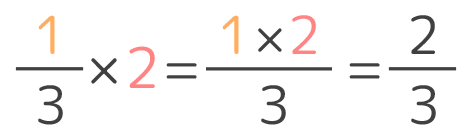
この「×2」を一番簡単な分数に書き換えるとどうなりますか？(▼をクリックして答を表示)

これを使って、13×2 を「分数×整数」から「分数×分数」に直すとどうなりますか？

この式を見ると、分子同士、分母同士をかけ算をしているのが分かります

つまり「分子同士・分母同士をかけ算する」というのが分数×分数のルールです。

「ホント？」という方は、もう一つの例を確かめて下さい。

足し算引き算に比べると、通分をしなくて良いので単純なルールだと思いませんか？

では、試しに1問練習してみましょう。

例題1(分数×分数)

今のやり方は、かけ算してから約分(割り算)をしていて二度手間ですね。

実は、分数×整数でやったように、分数のかけ算は、真上や真下だけでなく、斜め上や斜め下とも約分が出来ます。

先程の計算式の途中で、こんな形がでてきましたが

分子にある２と分母にある２を約分して(斜め上と斜め下でも約分ができるんです！)一気に答えが出せるのです。

この後は、途中で約分をしていきましょう。

 

実際の解き方/教え方

とにかく分数に苦手意識を持つ生徒が多いです(算数の成績が良い子でも)。

したがって分数を教えるときは「簡単だよ」という声かけをしながら実際に簡明なやり方を示し、それをステップを踏んで確実に解いていく感覚を身に着けさせましょう。

3ステップで解かせます。

❶準備
等号に続いて長い横線を書いて、そこに数値を移す

❷約分
分母と分子で約分が出来ないか調べて、実行させる

❸かけ算
分母同士・分子同士をかけ算して答えを出す。

「3ステップ」ということを明示し、1つの作業に集中させます。そして1ステップ終わるごとに意識的にリラックスさせて全体感覚(「あ、今のが全体の2番目だな。あと1つだな」)を取り戻させるのが重要です。

では、類題で練習して完全に身につけて下さい！

分数×分数の練習問題

やり方を確認するとこうでした。

このルールで計算して下さい。

●練問1-(1)

●練問1-(2)

●練問1-(3)

●練問1-(4)

●練問1-(5)

これで分数×分数の練習は終了です。途中で出てきたルールも入れてまとめると、こうなります。

次のステップへ