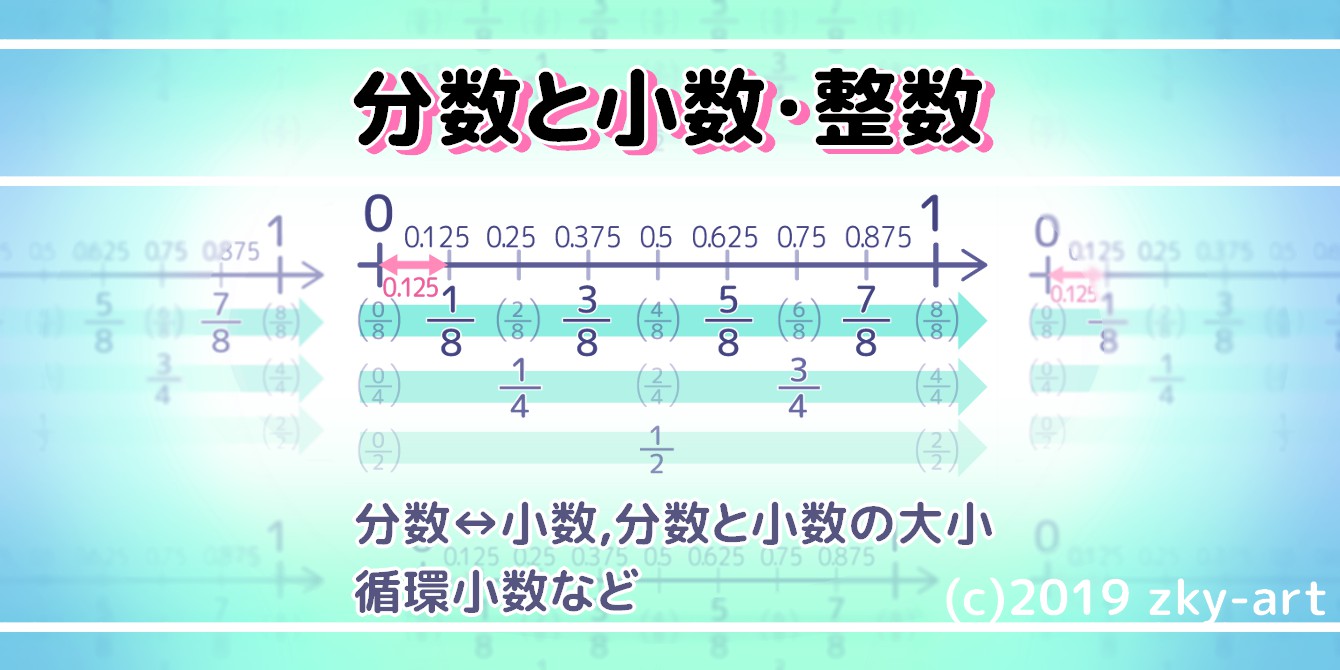
「分数を小数に変換したい」「分数を小数で表す方法が分からない」という小学5年生と保護者の方、お任せ下さい!東大卒講師歴20年の図解講師「そうちゃ」がまとめました
サッと見直したい人は目次の「まとめ」をクリックするとまとめに飛べますよ♪
目次(クリックでジャンプ)
整数から分数への変換(直し方)
 爽茶
爽茶こんにちは!「そうちゃ」@zky_tutor(プロフィール)です。
はじめはウォーミングアップに「整数を分数に直す」やり方です。
これはすごく簡単!今までに何度か出てきたコレです。
→「分母に1を付ければよい。
A=A1(例:7=71)
「整数を分数に直す」はコレで終わりです。
「5」を分数に直しなさい→( 51 )
 爽茶
爽茶分数から小数への変換(直し方)
分数のイメージその2「◯◯算」
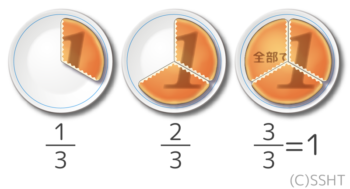
小4までは、分数「BA」の意味を「(1個のモノを)A等分したうちのBピース」とイメージしてきましたが
分数には、もう1つのイメージがあります。
それは割り算!
例えば「12」は「1÷2」と同じ意味です。
読み方は分母(下)から分子(上)ですが、わり算は逆に「上÷下」なのに注意して下さい。
→分数は割り算。上(分子)÷下(分母)
(例:2 3=2÷3)
「1÷2だったら「0.5」という小数があるんだから分数なんていらない!」と思うかもしれません。(分数が嫌いという生徒が本当に多いです)
でも「13」の場合はどうでしょう?わり算で1÷3を行うと「0.33333…」となって割り切れません。しょうがないので小数第3位を四捨五入して「0.33」などの概数で表すことになりますが、どうしても誤差がでてしまいます。
それに対して分数なら誤差なく表すことが出来るので非常に便利です。もともと分数はこの意味で発明されたそうですよ!
分数→小数の変換方法
今見たように、分数は割り算なので、割り算を計算(筆算)すると小数に直せます。
BA=B(分子)÷A(分母)
(例:12=1÷2=0.5)
試しに例題を解いてみましょう。
小数点が出る割り算を忘れた人は、過去記事「小数の割り算」を見直して下さい。
●例題1-(1)
割り算をするだけです。25=2÷5ですね。筆算で2の上に0を書くことに注意です。
5)20
20
40
0.4
●例題1-(2)
23=2÷3 なので筆算をすると…
3)2000
1800
0200
180
020
18
02
割り切れません!こういう問題は出題されないと思いますが、もし出た場合はしょうがないので0.666…と書きましょう。
0.666…
このような小数は「循環小数」と言って、本当は「0.6」のように数字の上に点をつけて表します。この記事の後ろの方で説明をしています。
 爽茶
爽茶簡単ですね?では、割り算の練習のつもりでもう少し練習して下さい。
この類題は全部割り切れるので安心して解いて下さい♪
「上÷下」ですよ!
練習問題で定着!
類題1(分数を小数に)
(1)35 (2)720 (3)1125
これで分数を小数に直せるようになりましたね!
次は分数と小数の大きさを比べてみましょう。
(応用)
分数と小数の大小比較
分数を小数に直せるようになったところで、その利用問題として「分数と小数の大きさ」を比べてみましょう!
比較のコツ=○○にそろえる
例題2(分数と小数の大小)
割り切れなくても焦らないで…
13=1÷3なので筆算をすると…
3)1000
900
100
90
010
9
01
割り切れません!
が、慌てずに問題をもう一度見て下さい。
この問題は「小数に直しなさい」ではなく「どちらが大きいか」答えればよいのです。
13=1÷3=3.33…で割り切れませんが、小数第一位で割り切れない時点で、3より大きいことは分かりますね!
3)10
9
11
どちらが大きいか(大小関係)が分かったら、それを不等号を使って表します。
不等号は左右の数のうち大きい方に「口を開ける」向きにします。
例えば「1と2の大小」なら「1<2」とか「2>1」になります。
この問題では、13の方が大きいので、13に口を開ける向きにします。
0.3<13
大小を比較する問題の解き方はわかりましたか?
割り切れなくても問題は解けるのです。
→分数を小数に直して比べる
(割り切れなくても大小が分かれば良い)
例:0.3と13の大小を比べる
13=1÷3=3.333→「0.3<13」
それでは、練習問題にチャレンジしてみて下さい。
練習問題で定着!
類題2(分数と小数の大小)
(1)0.8と56 (2)0.57と47
(3)0.24と415と14 (4)0.17と16と213
●類題2-(1)
●類題2-(2)
●類題2-(3)
簡単な分数から考えましょう
●類題2-(4)
先程のコワザを使うとミスが防げます。
分数から小数に直す問題はこれで終了です!次は今までと逆の、小数・整数から分数に直す問題です
小数から分数への変換(直し方)
「小数→分数」も、小数の意味をもう一回思い出せば簡単ですよ!
小数の大きさ(復習)
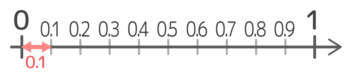
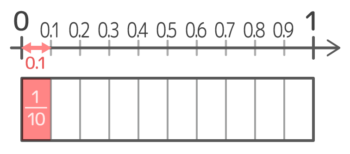
小数「0.1」はどういう大きさの数だったでしょうか?
つまり、0.1=110ということです。
同じように0.01=1100、0.001=11000 になります。
0.1=110 0.01=1100
0.001=11000
この考え方を使って、小数を分数に直してみましょう
直し方を考える!
●例題3-(1)
0.3と0.1の関係を考える
●例題3-(2)
小問1と同様に考える
小問(2)の問題と答えを並べるとこうなります。
これを見ると、もとの数「1.1」の小数点を取って「11」にして、下(分母)に「10」を付けただけと分かりますね!!
そう言えば小問(1)も…こうでした
「0.3」の小数点を取って「03」にして、分母に「10」を付けていますね(答えとして描く時は「03」を「3」にしないとバツなので注意)。
このルールで、小数第一位までの小数は簡単に仮分数に直せます。
小数を仮分数に直す
小数点を無くした数の並びにして
分母に10をつける。
(例:1.1=1110)
小数第二位までの小数はどうなるでしょうか?
●例題3-(3)
●例題3-(4)
●例題3-(5)
0.01を基準に考える
小問(5)の問題と答えを並べて見比べます
もとの数「1.11」の小数点を取って「111」にして、下(分母)に「100」を付けただけですね!!
そう言えば小問(4)も…
「0.11」の小数点を取って「011」にして、分母に「100」を付けていますね(答えとして描く時は「011」を「11」にしないとバツなので注意)。
このルールで、小数第二位までの小数も簡単に仮分数に直せます。
小数を分数に直す
小数点を無くした数の並びにして
分母に100をつける。
(例:1.11=111100)
例題で出てきたコワザ(小技)をまとめると、こうなります。
小数点を取った数の並びにして、
分母に10や100をつける
●小数点第1位までの数→分母に10をつける
●小数点第2位までの数→分母に100を 〃
●小数点第3位までの数→分母に1000を 〃
これで、どんな小数が出てきても分数に直すことが出来ますが、よく出る小数は暗記してしまう方がラクです。
ぜひ暗記しておいてほしいのは2つのシリーズです。
暗記する小数シリーズA(5等分)
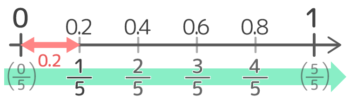
シリーズAは、数直線を5等分した0.2きざみの小数です。
0.2=15,0.4=25,0.6=35,0.8=45
この4つを覚えておきましょう。
例えば、1.8=145になります。
暗記する小数シリーズB(2,4,8等分)
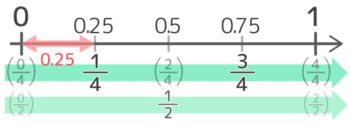
シリーズBは、数直線を2等分4等分した0.25きざみの小数です。
0.5=12,0.25=14,0.75=34
この3つを覚えておきましょう。
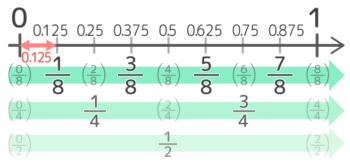
さらに、算数が好き得意な人や中学受験をする人は八等分も覚えておくと無敵です
0.125=18,0.375=38,0.625=58,0.875=78
この4つです。
では、力試しに類題を解いて見ましょう! これが全部できれば小数→分数は大丈夫でしょう。
練習問題で定着♪
●類題3-(1)
●類題3-(2)
●類題3-(3)
●類題3-(4)
よーく見て下さい
●類題3-(5)
●類題3-(6)
●類題3-(7)
●類題3-(8)
これで小数を分数に直す問題は終了です。
最後は、かなり応用です。分からなくても平気ですので気楽に読んで下さい。
(けっこう応用)
循環小数から分数への変換
「1÷3」の答えは割り切れず「0.333…」と続きますが、このような小数を「循環小数」と呼び、連続する数字の上に点をつけて「0.3」のように表します。
「0.3333…」→「0.3」と表す
「1.232323…」→「1.23」と表す
この循環小数を分数に直す場合はちょっと特殊なテクニックが必要になります。
算数が得意・好きな生徒さんと中学受験生向けです。
詳しくは姉妹サイト「そうちゃ式受験算数」の「小数の応用問題」内「循環小数の問題」を見て下さい。
 爽茶
爽茶まとめと確認テスト
この記事を確認テスト形式でまとめました。空欄をタッチすると答えが表示されます。
分数を小数にする
上(分子)÷下(分母)の割り算をする
(例)12=( 1÷2=0.5 )
小数を分数にする
→小数点を取った数の並びにして、分母に10や100をつける
●小数点第1位までの数
→小数点を取って分母に10をつける
_(例)1.1→(「11」の分母に10をつけて、1110)
●小数点第2位までの数→分母に100をつける
_(例)1.11→( 「111」の分母に100をつけて、111100)
●小数点第3位までの数→分母に1000をつける
_(例)1.111→(「1111」の分母に1000をつけて、11111000)
次のステップへ
 爽茶
爽茶分数と小数・整数の関係が分かりましたか?この後は新しい単元が次々連続で出てきます。このサイトを利用して、ちょっとでも予習をしておくと楽になりますよ!