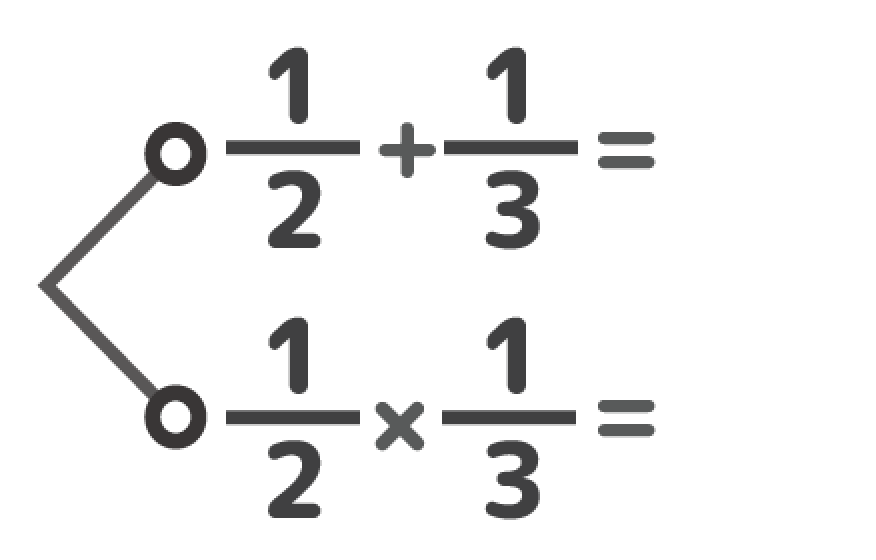「分数が嫌い、苦手」という小学6年生(または中学受験生)と保護者の方へ。20年の講師経験から実践的なアドバイスです。この記事を読んで少し練習すれば、分数への苦手意識が減って計算問題が「できる」ようになりますよ！
分数が苦手な小学5年生や保護者の方は「分数が苦手な小5への教え方」を御覧下さい。
目次(クリックでジャンプ)
なぜ分数が苦手になる！？
「分数の割り算」の説明よりも大事なこと
こんにちは！「そうちゃ」@zky_tutor(プロフィール)です。
ー(^o^)/~~小6の一学期に「分数と分数のかけ算・割り算」が出てくると「分数が苦手！分からない！」というお子さんが一気に増えます。
??( ³ω³ )??
ちなみに「分数のかけ算・割り算」をwebで調べると「分数の割り算はどうして逆数のかけ算になるのか」という説明ばかりです。
(私も関連記事で説明していますが(汗))
でも…「分数の割り算が逆数のかけ算になる理由」が分かっても問題が解けるようになるかは別の話ですね。それに「逆数のかけ算になる理由」自体が面倒くさい話なので分数に対する苦手意識は消えません。
(T_T)
また「分からない」「苦手」という小学生にかけ算・割り算をやらせて出来るようになっても、章のまとめの問題になると、やはり「分数が分からない・解けない・苦手」となってしまう。
(>_<)
実は、お子さんは「分数のかけ算や割り算」の理屈が分からないから苦手になっているのではないのです。
●この時期に分数が苦手になる理由
分数は小2から小3・小4の間はのんびりしたペースで学習しますが、小5になると「約分」→「通分」→「通分を使った足し算・引き算」→「分数と整数のかけ算」と分数が一気に進みます。
そして、分数計算で一番難しいのは実は「通分を使った足し算引き算」で、これをしっかり定着するのには訓練と定着時間が必要です。
ところが定着させる間もなく、次の単元である「分数と整数のかけ算割り算」が出てくるので、多くの小5が「通分のある足し算引き算」を消化不良のまま小6になってしまいます。
そこに追い打ちをかけるように(汗)「分数と分数のかけ算割り算」が出てきて、とどめに「分数の(足し算引き算かけ算割り算の)四則混合計算」が出てくるので、多くの小学生は頭が混乱して「ワケワカラン」になってしまうのです。
つまりこの時期に分数が苦手になるのは、小6になって出てくる「分数と分数のかけ算わり算」が難しいせいではなく、「かけ算(割り算)」と「足し算(引き算)」との「使い分け」ができないのが原因なのです。
ですから、分数が苦手な小6には
「かけ算・割り算」と「足し算・引き算」の違いを整理して定着させる
これが一番効果的です。
その上でで四則混合の計算練習をつめば「分数が全然分からない・解けない」ことはなくなるでしょう。
●スモールステップで教えましょう
「植木算の教え方」でも書きましたが、苦手な生徒に教えるときは一気に教えないで、理解定着に無理がない範囲で内容を分割して、定着期間(1日でも良い)をおいて教えましょう。
6年生で分数が苦手になった小学生には「かけ算割り算と足し算引き算の違い」→「分数の四則混合計算」という2stepで教えるのが良いでしょう。
(5年生の時から分数が苦手な人はコチラの記事を使って下さい。)
STEP1:
かけ算と足し算の違いを定着
分数の割り算はかけ算とほとんど同じで、引き算も足し算とほとんど同じなので、まず「かけ算と足し算の違い」を理解して定着させます。
この記事では、あとで復習・定着が図れるように復習素材にしていきます。
今回は「ダイソー」の大型の方眼カードを使いました。
1枚目のカード
カードの表側(穴が左側に来ます)の問題です(まだ書かないで下さい)。
・$frac{1}{2}$×$frac{1}{3}$=
それぞれの問題は簡単ですが、並べることで「違い」を頭に刻み込むことが出来ます。
参考記事「紛らわしい2つのものは並べてセットで覚える」「違い」を覚えさせるときは問題は簡単なものにします。さもないと混乱して逆効果になってしまいます。
さらにもう一押し、「足し算とかけ算の違い」を言葉で答える問題をカードに書き加えます。これで表は完成です。
②$frac{1}{2}$+$frac{1}{3}$=
③$frac{1}{2}$×$frac{1}{3}$=
算数のカードに言葉の暗記？と驚く方もいるかもしれません。
しかし、理社のような「暗記科目」以外でも、①のような重要な「やり方」「考え方」は意識的に暗記しないと定着しません。(もちろん、得意な子は自然に覚えますが)
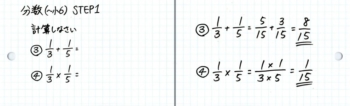
この問題をノートに説明して理解させながら、カードの裏を書きます。
カードの裏を書いたら、もう一度ノートに書きながら、声に出させます。こうして体(手と目と耳)に染み込ませます。
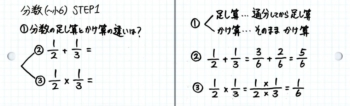
この時点で「そっか～。かけ算は足し算よりも楽だな」「なるほどね。通分が面倒くさいんだな」と生徒が実感できれば成功です。
もし、通分のある足し算が理解できていない場合は一旦戻って復習して下さい。当ブログの記事では「分母が異なる分数の足し算引き算」が参考になると思います。
2枚めのカード
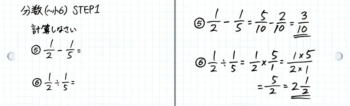
次にかけ算と割り算をカードにします。表はこんな感じ。
これを解かせながら裏に答えを書きます。
これで2枚めのカードも完成です。
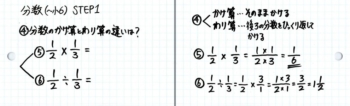
最低でも、この2枚のカードを作りましょう。
②で仮分数を帯分数に直していますが、それがサッと出来ない場合も一旦復習して下さい。当ブログの記事では「分数の種類。仮分数↔帯分数」が参考になると思います。
カードを作ったら、表側を見て①や④の文章は口に出し、問題は自力で正解できるまでノートに練習させましょう。
STEP1はコレで終了です！
追加のカード
生徒・お子さんに余力があれば、似た問題を出題して確かめても良いでしょう。
通分の練習にもなる簡単な問題が良いですね。例を挙げておくので参考にして下さい。
STEP1.5:
定着期間をとる
全部分からなくなるカードを作ったら定着期間をとります。
最低でも一日、苦手な子は三日は欲しいです。定着しないまま次にいくのは厳禁です。
定着期間は①の文章だけでなく②③の計算についても、カードの表を見たら裏の答えを途中過程も含めて全部を口で言えるようにします。
例えば「二分の一足す三分の一は、通分して六分の三足す六分の二だから六分の五！」という感じです。
この時「えーと…」とか言ってたらアウト！です(だから簡単な問題にしたんですね)。
誇張でなく、早口言葉のスピードで言えるようにさせて下さい(目安としては2秒以内)。教える側も一緒になって、どちらが早く言えるか遊んでもよいでしょう(私自身、生徒に負けないように時折早口言葉を練習していますｗ)。
こうして、かけ算と足し算(通分をする計算としない計算)の違いを頭と体に叩き込んだら、STEP2へ進みます。
STEP2:四則混合計算
始める前に、カードをサッと確認して万が一出来なかったら、その場で覚えさせます。
(^_^;)
STEP2では単純な分数で出来た四則混合問題を解いて、暗記した足し算引き算とかけ算わり算の「使い分け」を実際に使う練習をします。
1枚目のカード
1枚目のカードは小手調べ。
カッコを先に計算することを確認して、前から順に足し算、かけ算を計算します。途中で約分をすることに注意させます。
裏側を書きながら説明し、ノートに練習させます。
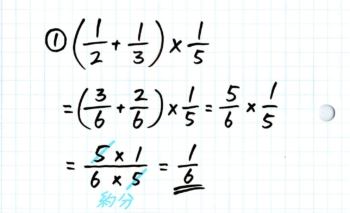
この時、計算する部分だけを書くのではなく、はじめの「×$frac{1}{5}$」のような計算しない部分も含めて、計算の全部分を「＝」の後ろに書き写していくようにします。
参考記事「入試で致命的な計算ミスを減らすには？」
生徒が表側を見て自力で正答できるを確認して1枚目のカードは終了です。
2枚目のカード
表側に問題を書きます。
はじめの足し算を計算してしまう生徒が多いので、かけ算をはじめに計算することに注意させましょう。
裏側に答えを書きながら説明し、ノートに練習させます。
この時、かけ算を「かっこ」で囲むクセをつけておくと計算ミスが激減します。
表側を見て自力で解けたら、2枚めのカードも終了です。
3枚めのカード
わり算と引き算の組み合わせです。
わり算を先に計算するので、前から計算するだけです。
ただ先程述べたように、かけ算わり算をカッコで囲んだ方が良いです。「カッコをつけなくても同じでしょ」と生徒が言っても「あなたの為だから！ね！書こうね！」と言って書かせましょう。
(^_^;)
参考記事「入試で致命的な計算ミスを減らすには？」
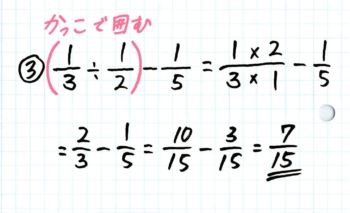
自力で正答できたら3枚目も終了。次が最後のカードです。
4枚目のカード
最後も引き算とわり算ですが、順番に気をつけさせましょう。
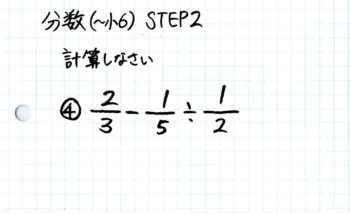
ここでもわり算をカッコで囲むことで計算ミスを最小限に抑えます。
これで終了です！
この4枚のカードが解ければ、分数の足し算引き算とかけ算わり算の「使い分け」自体は出来ているので分数計算がワケワカラン状態からは脱しているはずです。
後は普段使っている問題集の「分数の足し算引き算」と「分数と分数のかけ算割り算」の単元で問題演習をすれば、四則混合計算も徐々にできるようになってくるでしょう。
当ブログの記事「分数の四則混合計算」にも問題がありますのでご利用下さい。
残る問題
先程は扱いませんでしたが、「小数と分数」も嫌いな生徒さんが多いです。
計算で使うのは「小数→分数」なので、今回は「小数→分数」の暗記すべき基本だけ示します。詳しくは当ブログの「分数整数小数の混合計算」内のコチラが参考になると思います。
見直し用にカードにすると表はこんな感じ。
②0.25を分数にせよ
③0.375を分数にせよ
裏はこんな感じ
②0.25=$frac{25}{100}$=$frac{5}{20}$=$frac{1}{4}$
③0.375=$frac{375}{1000}$=$frac{75}{200}$=$frac{15}{40}$=$frac{3}{8}$
「分数に直して約分」という処理を身につけるのが目的です。
分数が苦手では無くなりましたか？
最後まで読んでいただきありがとうございました。この記事を参考にあなたの生徒さんお子さんの「分数嫌い」が少しでも直ったら嬉しいです！
2023年度生徒さん募集
2023年度の生徒さんの募集を開始しました(対面授業の一次募集)
東武野田線・伊勢崎線沿線にお住まいの新5年生で予習シリーズをベースにされている方が対象です。
詳しくはコチラのページを御覧下さい
新4年生の方を対象に学習相談/授業を実施します(2次募集はサピックス新越谷校・南浦和校の方のみ対象。締め切り1/27)。応募はコチラから
中学受験でお悩みの方へ
爽茶「中学受験と高校受験とどちらがいいの？」「塾の選び方は？」「4年次・5年次はどう勉強すればよい？」「志望校の過去問が出来ない…」など
様々なお悩みへのアドバイスをまとめたので参考にして下さい。
もしかしたら、自分だけで悩んでいると煮詰まってしまい、事態が改善できないかもしれません。講師経験20年の「そうちゃ」に相談してみませんか？対面/オンラインの学習相談を受け付けているので、ご利用下さい。