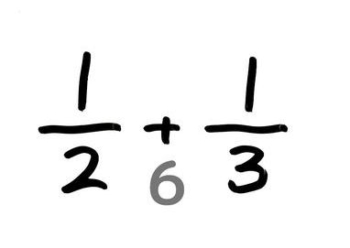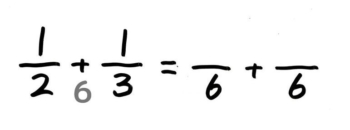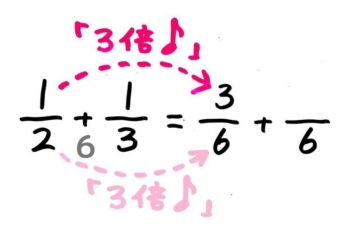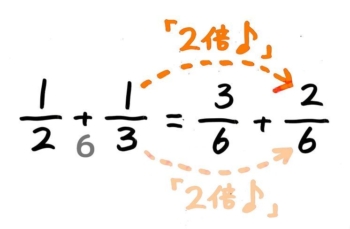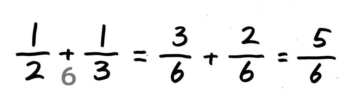分母が違う分数の足し算が苦手な小学5年生の方、「なんで出来ないんだろう…」と不安になったり焦っていませんか？
実は、分数で一番難しいのが「分母が違う分数の足し算引き算」
「分数のくり上がり」や「通分」など今まで習ったことが全部身についてないとできないからです。
でも大丈夫。この記事では東大卒講師歴20年の図解講師「そうちゃ」が必要な知識を一つづつ分かりやすく説明します。
記事の中の問題を解いているうちに「分母が違う分数の足し算引き算」がスラスラ解けるようになっているでしょう。
歴史を学習する小学生の保護者の方へ
年表,年号,地図,書き取りテストなど400枚のプリントがセットになったそうちゃ式オリジナル教材が8/25(日)までお買い得価格！興味がある方はコチラへ
(復習)分母が等しい分数
の足し算・引き算
爽茶
分数の足し引きの基本ルール
4年で学習した「分母が同じ分数の足し算引き算」のルールを簡単に復習します。
帯分数の足し算・引き算
整数と分子同士を足し引きする。
（分母はそのまま)
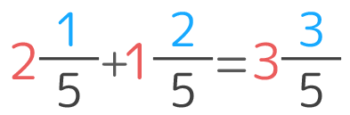
思い出しましたか？「分母は足し算引き算をしない」のがポイントでしたね！
分数の繰り上がり・繰り下がり
実はもう一つ大切な事がありました。それは「帯分数の整数部分の繰り上がり・繰り下がり」です。「え？何だっけ？」という人は練習しながら思い出しましょう。大丈夫な人はとばして先に進んで下さい。
●例題1-(1)
175+367を計算しなさい。
図解
解答を表示
157+367=4117 ですが、分数部分117が仮分数になっていますね。
そこで117を帯分数に直すと147 になるので、元の整数部分4と足して(分数のくり上がり)、547が答えになります。
整数部分が4から5にくり上がる。
4117→4+117→4+147→547
答:547
途中で出てきた、仮分数から(への)帯分数への(からの)直し方を復習したい人は参考記事「分数のまとめ」内「分数の種類」を見直して下さい。
●例題1-(2)
429－249 を計算しなさい。
図解
解答を表示
このままだと、分子同士の引き算が2-4で出来ません。
そこで429の整数部分4を3と1に分けて,その１を99にして元の分数部分29と足して119にすると3119になって分子が2から11へ大きくなります。(分数のくり下がり)
分数のくり下がり
429→3+1+29→3+99+29→3119
これで計算ができます。
429-249＝3119－249=179
答:179
●例題1-(3)
4-156を計算しなさい。
図解
解答を表示
分数部分の引き算を見ると、このままでは出来ませんので、整数部分を繰り下げて分数を作ります。
4を3と1に分けてから、1を66にして再び3と合わせて366にします。
繰り下げて分数を作る
4→3+1→3+66→366
これで引き算ができます。
4-156＝366-156＝(分数部分は6-5=1、整数部分は3-1=2)＝216
答:216
爽茶
思い出しましたか？もっと詳しく復習したい人は参考記事「 分数のまとめ」内「分数の足し算引き算」を見直して下さい。
「大丈夫！」な人は、今回の本題「分母が異なる分数の足し算引き算」に進みましょう♪
分母が異なる分数同士の
足し算
爽茶
今までは「分母が同じでない分数の足し算引き算はできない」と言われていましたね？
今回から分母が異なる分数でも足し算引き算ができるようになりますよ！
異分母分数の足し算のルール(通分)
例題2(異分母分数の足し算)
次の式を計算しなさい。
12+13
図解
分母が違う場合、そのままでは足し算引き算はできません。
なぜなら、12はパンを二等分したものが１ピース、13は三等分したものが１ピースというふうに、１ピースの大きさが違うからです。
分母が違うと分け方も違う
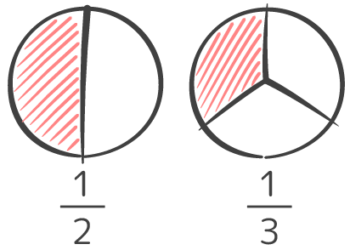
そこで、足し算・引き算をするために「等分の仕方」つまり分母をそろえる(通分する)必要があります。
通分とは、分母に使われている異なる数字の最小公倍数を求め、それに合わせて分子も整数倍することでした(「約分」の反対で「倍分」)。通分が思い出せない！という人は前回の記事「通分」を見直して下さい
さて、この小問では、分母は２と３で最小公倍数は６なので、12と13 を分母が６になるように倍分します。
12は分子分母を３倍して36に、13は分子分母を2倍して26にします。
通分の手順
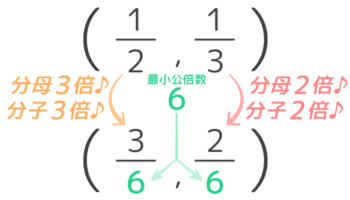
慣れるまでは声に出すと良いですね
これで分母が6にそろって、1ピースの大きさが同じになったので、足し算ができます。
分母が同じなら分け方も同じ
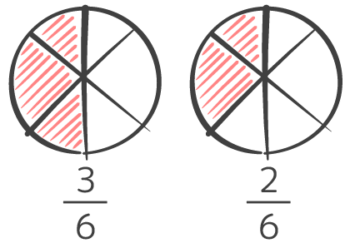
12+13＝36＋26=56
答:56
分かりましたか？
分母が異なる分数の
足し算引き算
通分してから、分子だけを足し算・引き算
12+13=26+36=2+36=56
爽茶
通分をした後は4年生の時と同じで分子だけを足し算すればよいのです。簡単ですね！
次は実際に解く時の注意を書きますが「早く問題を解きたい！」という人は
ジャンプして下さい。
実際の解き方・教え方
実際に解く時は、次のようなステップで、ステップごとに集中させるとミスがなくなります。
❶最小公倍数を求める。
式を書き写し、離れた余白で最小公倍数を求めて式の下にメモします。慣れてきたら、このステップは飛ばしても良いです。
❷通分の準備をする(これが大切！)。
問題文(式)から等号(=)を書き、最小公倍数を分母に、分子は空白の分数を書く。
今から6に通分するぞ！と集中させる
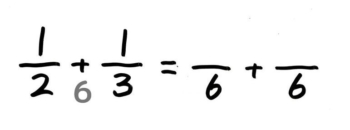
❸通分作業
まず、1番目の分数の分母から通分先の6を指でたどって「◯倍」と唱えさせます。
一緒に楽しく唱えましょう♪
つぎに分子を指でたどって「◯倍」と唱えて分子を計算して書きます。
「3倍」と唱えて(同時に)1×3を計算させる
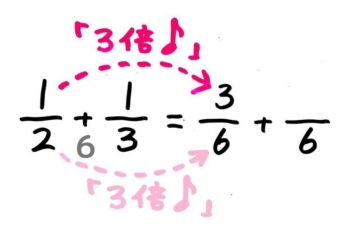
2番めの分数も分母・分子の順に「●倍●倍♪」と唱えながら計算して分子を書きます。
「2倍♪2倍♪」と唱えて1×2を計算
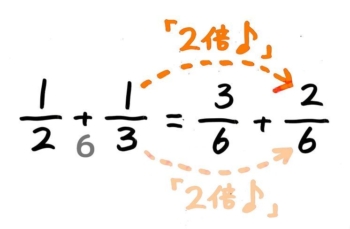
❹足し算引き算
分子のみを足し算引き算して答えを出します。
慣れてくれば、一瞬で出来るようになる子が多いですが、初めはこのようにステップに分けて確実に処理させて「よし、出来る」という自信をもたせましょう。
爽茶
このサイトでは何度も言っていますが(汗)、分数が嫌いな生徒が本当に多いです。実際、分母が異なる足し算引き算は一番面倒くさいところなので、「●倍♪●倍♪」と保護者・教師も一緒になって作業自体を楽しんで、分数に対する拒否感を無くしていきましょう。
では、類題で練習しましょう！
練習問題で定着！
●類題2-(1)
13+15=
図解
解答を表示
計算の全体像は次の通りです。
分母が３と５、最小公倍数は15です。分母が15になるように13と15を倍分します。
13は分子分母を5倍して515に、15は分子分母を3倍して315にします。
これで、分母がそろったので、足し算をして515＋315=815 です。
答:815
●類題2-(2)
34+56=
図解
解答を表示
分母が4と6、最小公倍数は12なので、分母を12に通分します。
34は分子分母を3倍して912に、56は分子分母を2倍して1012にして通分が完成。
足したものを帯分数に直して終了です。1912→1712
計算の全体像
34+56=912＋1012=1912=1712
答:1712
●類題2-(3)
123+34=
図解
解答を表示
分母が3と4、最小公倍数は12なので、分母を12に通分しますが、帯分数は分数部分(分子分母)のみを倍分するのに注意です。
123は整数部分の１はそのままで分子分母を4倍して1812に、34は分子分母を3倍して912になります。
足し算の結果を仮分数を帯分数に直して、整数部分に繰り上げます。
1812＋912=11712→1＋1712→1+1512→2512
計算の全体像
123+34＝1812＋912=11712=2512
答:2512
●類題2-(4)
56+310=
図解
解答を表示
分母が6と10、最小公倍数は30なので、30に通分します。
56は分子分母を5倍して2530に、310は分子分母を3倍して930になります。
足し算して仮分数を(約分してから)帯分数に直したものが答えです。
2530＋930=3430→(2で約分)→1715→(仮分数に直す)→1215
計算の全体像
56+310=2530＋930=3430
=1715=1215
答:1215
●類題2-(5)
12+123+34=
ヒント
3つの分数の足し算は、一気に通分した方がラクな事が多いです。
図解
解答を表示
2,3,4の最小公倍数である12に通分して足し算し繰り上げをして答えを出します。
計算の全体像
312+112+34=3612+1812+912
=42312=51112
答:51112
爽茶
これで足し算は終了です。次は引き算です。
分母が異なる分数の引き算
異分母分数の引き算のルール
爽茶
引き算も足し算と同じで「通分」をしますが、この記事のはじめに復習した「分数の整数部分のくり下がり」に注意します。
例題3(異分母の分数の引き算)
312－223 を計算しなさい。
図解
2と3の最小公倍数6に通分します。
312は整数部分3はそのままで、分子分母を3倍して336に、223は整数部分2はそのままで、分子分母を2倍して246にします。
しかし、そのままの引き算336では分子の引き算が出来ないので、336の整数部分を繰り下げて296にします。
分数の繰り下がりで分子を3から9にする
336→2+1+36→2+66+36→296
これで引き算ができますね。
312－223=336－246=296－246=56
答:56
分かりましたね！さっそく類題で練習しましょう！
練習問題で定着♪
●類題3-(1)
13ー15 を計算せよ
図解
解答を表示
分母が３と５なので最小公倍数15に通分すると、13は分子分母を5倍して515に、15は分子分母を3倍して315になります。
あとは同分母の引き算をして13–15=515–315=215ですね。
計算の全体像
13–15=515–315=215
分母の3と5を15に通分
答:215
●類題3-(2)
516－289 を計算せよ
図解
解答を表示
6と9の最小公倍数18に通分します。
516は5318に、289は21618になりますが、分子を見比べると、引き算が出来ないので、5318の整数部分5から１を分数部分に繰り下げて42118にします。これで引き算ができます。
計算の全体像
516–289=5318–21618
=42118–21618=2518
通分して繰り下げてから引き算
答:2518
●類題3-(3)
356－113－815 を計算せよ
図解
解答を表示
6と3と15の最小公倍数は30に通分します。
356は32530に、113は11030に、815は1630になります。
途中、分子の引き算が出来ないので繰り下げを行って計算します。
計算の全体像
356-113–815=32530-11030–1630=
=21530–1630=14530–1630=12930
通分して繰り下げて引き算
答:12930
これで引き算もOKですね♪次は、混合問題に挑戦して下さい。
足し算引き算の混合計算
爽茶
通分する足し算引き算は出来るようになったので、足し算引き算が混じった計算をやってみましょう♪
●類題4-(1)
216－1710+34
図解
解答を表示
3つの分数は分母(6,10,4)の最小公倍数の60に通分します。
途中、分子の引き算ができないので繰り下げを行い計算します。
計算の全体像
216－1710+34=21060－14260+4560=
=17060－14260+4560=2860+4560=7360=11360
通分して繰り下げて引き算
答:11360
●類題4-(2)
1121+914－3435
図解
解答を表示
3つの分母21,14,35の最小公倍数210に通分します
(これくらい大きくなってくると「すだれ算」を使うと安心できます。すだれ算に興味がある人は「すだれ算」「3つの数のすだれ算」を見て下さい)。
途中はずっと仮分数のまま計算して最後に帯分数にします。
計算の全体像
1121+914－3435=110210+135210－204210=
=245210－204210=41210
210に通分して計算
答:41210
汚い答えになってしまいました。ｽｲﾏｾﾝ
●類題4-(3)
(12－49)+(56－34)
ヒント
「かっこ」がありますね
図解
解答を表示
前のカッコの中は分母(2,9)の最小公倍数18に通分して計算し、後ろのカッコの中も分母(6,4)の最小公倍数12に通分して計算します
最後に2つのカッコの結果を18と12の最小公倍数36に通分して足し算します。
計算の全体像
(12－49)+(56－34)=(918－818)+(1012－912)=
=118+112=236+336=536
まずカッコの中を通分して計算
答:536
次は、分数と小数・整数の混合問題です。これが出来れば、分数の足し算引き算はもう完璧です！
小数・整数との足し算引き算
爽茶
分数・小数・整数が混じった計算は、まず小数を分数に直してから計算します。
小数を分数に直す方法(復習)
小数を分数に直す方法をもう一度確認します。こうでした。
小数→分数
小数点を取った数の並びにして、分母に10や100をつける
●小数点第1位までの数→分母に10をつける
●小数点第2位までの数→分母に100を 〃
●小数点第3位までの数→分母に1000を 〃
爽茶
このルールを使えるか確認します。「大丈夫！できるよ！」という人は
先に進んで下さい。
●例題5-1
1.3 を分数に直しなさい。
図解
解答を表示
「1.3」から小数点を取って数の並びにすると「13」
「1.3」は小数点第一位までの数なので「13」に分母「10」をつけて、310になります。これを帯分数に直して1310が答えになります。
答:1310
コワザ
今は初めに仮分数で求めましたが、「1.3」を「1+0.3」に分けて、「0.3」を数の並び「3」に分母「10」をつけて310と直してから、1を足して1310と出すやり方でも良いです。
別解
1.3=1+0.3=1+310=1310
1.3を分数に直す
この後は、こちらのやり方で解いていきます。
●例題5-2
2.15 を分数に直しなさい。
図解
解答を表示
「2.15」を「2」と「0.15」に分けて「0.15」を分数にします。
「0.15」は小数第二位までの数なので、数の並び「15」に分母「100」をつけて、15100になりますが、これで終わりではありません。
15100は分子分母を5で約分すると320になるので、
最初に分けていた整数「2」をつけて2320が答えです。
答:2320
●例題5-3
1.8 を分数に直しなさい。
図解
解答を表示
1.8を「1」と「0.8」に分けて「0.8」を分数にします。
「0.8」は小数第一位までの数なので、数の並び「８」に分母「10」をつけて810。これを約分して45
答:45
コワザ
上のように解いても間違いではありませんが、0.2,0.4,0.6,0.8という0.2刻みの数は15,25,35,45というふうに暗記してしまうのをオススメします。
0.2刻みの小数は分母が5の分数になる
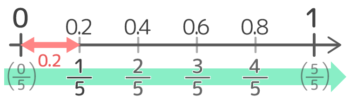
この後は、こちらのやり方で解いていきます。
●例題5-4
3.25 を分数に直しなさい。
図解
解答を表示
3.25の「0.25」を小数に直します。
「0.25」は小数第二位までの数なので、数の並び「25」に分母「100」をつけて25100 。これを約分して14で、３と合わせて314
答:314
コワザ
上のように解いても間違いではありませんが、0.25,0.5,0.75という0.25刻みの数は14,24=12,34というふうに暗記してしまうのをオススメします。
0.25刻みの小数は分母が4の分数になる
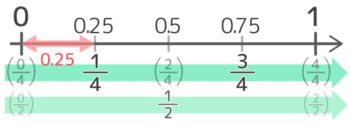
この後は、こちらのやり方で解いていきます。
●例題5-5
1.375 を分数に直しなさい。
図解
解答を表示
1.375の「0.375」を小数に直します。
「0.375」は小数第三位までの数なので、数の並び「375」に分母「1000」をつけて3751000。これを約分して38で、1と合わせて138です。
答:138
コワザ
上のように解いて良いですが、算数が好き得意な人や中学受験生は、0.125,0.375,0.625,0.875という0.125刻みの数は18,38,58,78というふうに暗記してしまうのをオススメします。
0.125刻みの小数は分母が8の分数になる
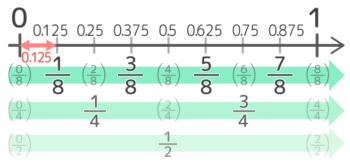
この後は、こちらのやり方で解いていきます。
爽茶
これで、小数から分数への直し方は思い出せましたね？
では、実際に分数・小数・整数の計算をしてみましょう。
練習問題で定着
●類題5-1
2.7+815を計算しなさい
図解
解答を表示
2.7を分数に直した2710と815を最小公倍数30に通分して足し算すると23730になります。
分子が分母より大きいので繰り上げて3730が答えです。
計算の全体像
2.7+815=2710+815
=22130+1630=23710=3710
分数にして通分して足し算
答:3730
●類題5-2
3.75－56 を計算しなさい
図解
解答を表示
3.75を分数に直した334と56を分母(4,6)の最小公倍数12に通分すると 3912–1012 になりますが、分子の引き算が出来ないので繰り下げてから引き算した21112が答えです。
3.75－56=334–56=3912–1012=22112–1012=21112
計算の全体像
3.75－56=334–56=3912–1012
=22112–1012=21112
繰り下げしてから引き算
答:21112
●類題5-3
(4.5- 213)+1.125 を計算しなさい
ヒント
カッコがあります
図解
解答を表示
4.5を分数に直した412から213を引いた答えの216に1.125を分数に直した118を足した3724が解答です。
計算の全体像
(4.5- 213)+1.125=(412-213)+118
=(436-226)+118=216+118=2424+1324=3724
通分を2回行います。
答:3724
●類題5-4
5-(347－1.4) を計算しなさい
図解
解答を表示
1.4を分数に直した125を347から引いた答え2635を5から引いたが22935答えです。5を繰り下げて43535にしてから計算します。
5-(347－1.4)=5-(347－125)=5-(32035－11435)=5-2635=43535-2635=22935
計算の全体像
5-(347－1.4)=5-(347－125)=
5-(32035－11435)=5-2635=43535-2635=22935
5を繰り下げてから計算する
答:22935
これで計算は終了です！もっと練習したい人には、記事の一番下でオススメ教材を紹介しています。
次はこの記事の最後！文章問題です。
文章問題
爽茶
最後は文章問題です。文章問題を解く時は簡単な図や絵を描くと分かりやすく楽しいのでオススメです！
●文章題-1
ジュースが56Lあります。Aさんが飲んだら残りが34Lになりました。Aさんは何L飲みましたか？
ヒント
問題を読んだら、いきなり計算をせずに、図や式を書いて、方針を立てましょう。
図解
解答を表示
56–34=1012–912=2112
答:112L
●文章題-2
Bさんは家から313km離れた公園まで歩いて行きました。帰りも同じ道で家に向かっていましたが、家から1.8kmのところで迎えに来たお父さんの車に乗って帰りました。Bさんは行き帰り合計で何km歩きましたか？
ヒント
問題を読んだら、いきなり計算をせずに、図や式を書いて、方針を立てましょう。
図を表示
こんな感じですね
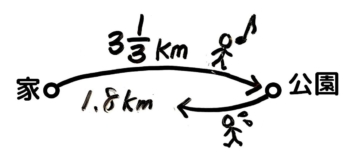
図解
解答を表示
問題文の状況を図にするとこんな感じです。
ここまで細かく書く必要はありません
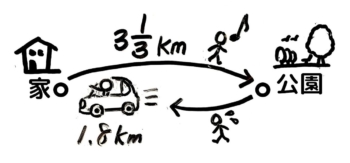
Bさんが歩いた距離は、往復の距離313km+313kmから、車に乗った1.8kmを引いたものなので、313+313-1.8になります。
1.8を分数145に直して計算を始めます。
313+313-1.8
=313+313-145
=623–145=61015–11215=52515–11215=41315
答:41315
(2)までが簡単すぎた人のために、(3)は少し難しいですよ！
●文章題-3
容器にフワフワ粘土が入っています。まずAさんが5.75g、次にBさんが612gの粘土を容器から取りました。最後に先生が容器に粘土を213g足したところ、容器の中の粘土はちょうど10gになりました。はじめに容器の中には何gの粘土が入っていましたか？
ヒント
頭の中だけで考えようとするとゴチャゴチャしてくるので、実体図や線分図にしてみましょう。
実体図を表示
左から右へ書いてゆく
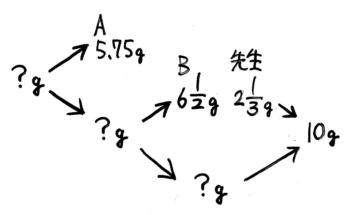
図解
解答を表示
状況を図にすると、こうなります。
ここまで詳しく書かなくても良い
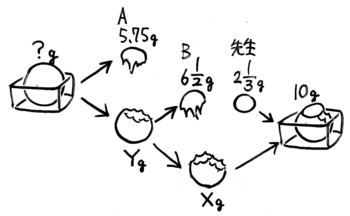
最後の重さが分かっているので、最後の10gから時間を戻るように計算していきます。途中をXとYと名付けました。
先生が足す前の重さ(X)は、10-213=933-213=723
Bさんが取る前の重さ(Y)は、723+612=746+636=1376=1416
Aさんが取る前の重さ(?)は、1416+5.75=1416+534=14212+5912=191112
答:191112
これで問題は全て終了です。お疲れ様でした！
まとめ
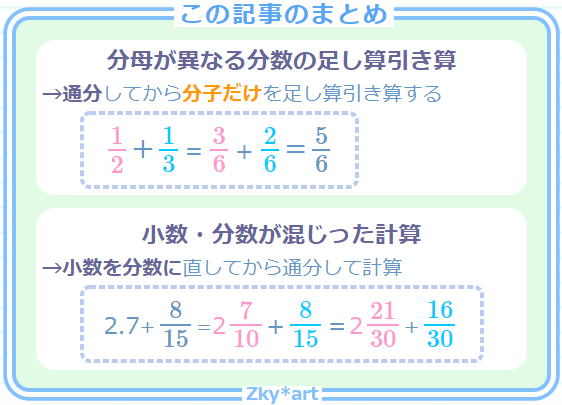
爽茶
分母の異なる分数の足し算引き算は分かりましたか？
これで、分数計算で一番面倒くさいところは終了です！「分数のまとめ」から「分数のかけ算わり算」に進んで下さい。
オススメ教材
爽茶
もっと問題を解きたい！という人にオススメ教材を紹介します。
動画で学習したい人へ
「分かりやすい！」と評判の
スタディサプリなら有名講師「尾﨑 正彦」氏による分数のたし算ひき算の授業動画もありますよ♪
今なら
14日間無料♪この期間内に利用を停止すれば料金は一切かかりません。この機会に試してみては？
歴史を学習する小学生の保護者の方へ
年表,年号,地図,書き取りテストなど400枚のプリントがセットになったそうちゃ式オリジナル教材が8/25(日)までお買い得価格！興味がある方はコチラへ
2023年度生徒さん募集
2023年度の生徒さんの募集を開始しました(対面授業の一次募集)
東武野田線・伊勢崎線沿線にお住まいの新5年生で予習シリーズをベースにされている方が対象です。
詳しくはコチラのページを御覧下さい
新4年生の方を対象に学習相談/授業を実施します(2次募集はサピックス新越谷校・南浦和校の方のみ対象。締め切り1/27)。応募はコチラから
中学受験でお悩みの方へ
爽茶
いつもお子さんのためにがんばっていただき、お疲れ様です。
中学受験を考えると色々と悩みが出てきますね。
「中学受験と高校受験とどちらがいいの？」「塾の選び方は？」「4年次・5年次はどう勉強すればよい？」「志望校の過去問が出来ない…」など
様々な
お悩みへのアドバイスをまとめたので参考にして下さい。
もしかしたら、自分だけで悩んでいると煮詰まってしまい、事態が改善できないかもしれません。講師経験20年の「そうちゃ」に相談してみませんか？対面/オンラインの学習相談を受け付けているので、ご利用下さい。
最後まで読んでいただきありがとうございました♪この記事があなたの役に立てたなら嬉しいです!
