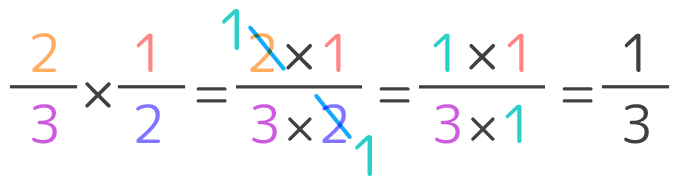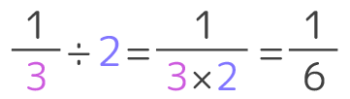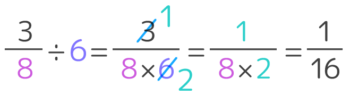「分数と分数の割り算のやり方が良くわからない」「逆数をかけるのはなぜ?」という小学6年生の方、お待たせしました!東大卒講師歴20年の図解講師「そうちゃ」が分かりやすく教えます♪この記事を読めばスラスラ解けるようになりますよ
目次をクリックすると読みたいところに飛べますよ♪
目次(クリックでジャンプ)
分数と整数のわり算(復習)
 爽茶
爽茶こんにちは!「そうちゃ」@zky_tutor(プロフィール)です。
「分数÷分数」の前に「分数÷整数」をちょっとだけ復習します。小学5年生の三学期に「分数と整数のかけ算・わり算」を学習しました。復習としてまとめると、こんな感じでした。
「分母にかけ算」というのが特徴でした。だいたい思い出せたら「分数÷分数」をはじめましょう。
分数÷分数のやり方を理解
分数の割り算は○○算になります
簡単なクイズです。今、分数÷整数の割り算がありましたが、
この「2」を一番簡単な分数に書き換えて、さきほどの式を「分数÷整数」から「分数÷分数」に直すとどうなりますか?
以前勉強したA<=A1 を使って 2=21 と直せば分数÷分数に書き換えられます!
そして、答えは変わらず16のハズですから、
という式ができますね。この式の答えの分母の6は13の分子「3」と12の分母「2」のかけ算で出来ていました。
分子と分母をかけていたんですね。
では答えの分子の1はどこから出てきたのか?というと…13の分子「1」と12の分母「1」のかけ算で出来ているのです。つまり…
こういう計算をしていたのですね。
ちょっと長くなりましたが…このように分数÷分数の場合、「÷」の後ろの分数の分子と分母をひっくり返したものをかけ算すれば良いのです。
ちなみに、この「分数の分子と分母をひっくり返した数」を逆数(ぎゃくすう)と言います。
❶分子分母をひっくり返してわり算をかけ算にする

❷分母と分子をひっくり返した数=逆数
(例)23の逆数は32
 爽茶
爽茶これでやり方は分かったと思いますが…
「なんで割り算がかけ算になるの?」と思う人のために説明をしてみます。
「それより問題を解きたい!」という人はジャンプして下さい。
逆数をかける理由
理由を説明する理由
突然ですが質問です!
私の20年間の講師生活で「分数の割り算がどうして逆数のかけ算になるのか?」という質問を受けたことが何回くらいあると思いますか?小学生に戻ったつもりで考えて下さい。
分数の足し算引き算って通分があって面倒くさかったですね? ですから、かけ算わり算を習う前は「あんなに大変だった足し算引き算の後に来る分数のかけ算わり算は、どんなに難しいんだろう…分からなかったらどうしよう…」とビクビクしていませんでしたか?
そんな時に先生(私)から「かけ算わり算の方が簡単だよ♪」「分子・分母同士かけるだけだよ!」「ひっくり返してかけるだけだよ!!」と説明されたとしたら…「どうして?!」なんて質問をするでしょうか?それよりも「そんな簡単でいいの?!良かった!!」と驚き・安心して、問題を解こうとしますよね?
というわけで…質問の答えに戻ると、20年間で「分数の割り算がどうして逆数のかけ算になるの?」と質問する生徒はほとんどいませんでした!!(というかゼロだと思う…)
ですから、この記事を書くための事前調査で、ネットでは「分数の割り算がどうして逆数のかけ算になるのか?」の説明があふれかえっていることには少し驚きました…がネットにあふれかえっているということは知りたい方が多いという事ですから…当ブログでも説明をしてみよう、というわけです。
説明その1
一番最初に習った分数の意味を思い出してみましょう。
12=二等分したうちの一つですから「6×12」は6を二等分したうちの一つで、「6÷2」と同じ意味ですね。
そして2=21なので「6÷2」と「6÷12」と「6×21」は全部同じ意味です。
というわけで÷12と ×21 は同じ意味になり分数の割り算は「逆数をかける」と同じと分かります。(これは、三角形の面積などで感覚的に使い慣れていますよね!)
★三角形の面積=底辺×高さ÷2=底辺✕高さ×12
説明その2
理由その1で納得してほしいのですが…純粋に計算式上で考えるとこうなります。分数BAのもう一つの意味は「B÷A」なので「10÷42」は「10÷(4÷2)」と同じ意味で、答えは「10÷(4÷2)」=>10÷2=5になるはずです。
ところで、「10÷(4÷2)」の(4÷2)の「かっこ」を外すと「10÷4×2」 と「 10÷4÷2」 のどちらになるでしょうか?答えが5になる方が正解なので 「10÷4×2」 の方ですね。
そして「10÷4×2」 を分数にすると「104×2=10×24」になり、「10×24」の10をかけ算として前に出すと「10×24」と直せます。
このようにして、分数の割り算「10÷42」を「10÷(4÷2)」→「10÷4×2」→「10×24」→「10×42」と逆数の掛け算に直せました。
10÷42=10÷(4÷2)=10÷4×2=10×24 =10×42
中学で10-(4-2) の「カッコ」を外すと 10-4+2 になる(マイナスを引くとプラスになる)のを学びますが、それと同様(割り算を割るとかけるになる)です
というわけで、少し話がそれましたが(汗)、分数÷分数の計算を類題で練習します。その前に…
実際の解き方と教え方
「どうしてかけ算になるのか」よりもずっと大事なのが「実際の計算を素速く正確に行う手順」です。
分数に苦手意識を持つ子が多いので「ほとんど、かけ算と同じだよ!」「簡単だよ!」と明るく楽しい雰囲気で解かせましょう。
実際、かけ算と同じ3ステップです。
手順(3ステップ)
❶準備
等号に続いて長い横線を書いて、そこに数値を移す。この時、割り算の分数は分子・分母を上下逆に移す
13÷56=5555555555
13÷56=1 x 63 x 5
*本当にはじめのうちは、分数の掛け算に書き直してから数値を移しても良いですが、慣れてきたら書き直さずに直接移しても良いでしょう。
❷約分
分母と分子で約分が出来ないか調べて、実行させる
1 x 63 x 5=1 x 21 x 5
❸かけ算
分母同士・分子同士をかけ算して答えを出す。
1 x 21 x 5=25
かけ算の時と同様に、1つの作業に集中させて1ステップ終わるごとに全体感覚(「あ、今のが全体の2番目だな。あと1つだな」)を取り戻させるのが重要です
以上を頭に入れて、類題で練習しましょう。
分数の割り算を練習
もう一度解き方を確認します。
❶分子分母をひっくり返してわり算をかけ算にする

これを参考に問題を解いて下さいね。
●練問2-(1)
ルール通り計算すればOK
簡単ですね?
●練問2-(2)
●練問2-(3)
◯分数は●分数に直しましょう
●練問2-(4)
答える前に…
●練問2-(5)
答える前に注意
●練問2-(6)
整数も◯分数に直す
これで分数と分数のわり算も終了です。もう一度まとめます。
❶分子分母をひっくり返してわり算をかけ算にする

❷整数と帯分数は仮分数に直して計算
❸計算途中で約分をしてもよい
❹答えるときは帯分数に直す
これで分数÷分数の計算は大丈夫ですね!
かけ算・わり算の混合計算
 爽茶
爽茶かけ算・わり算が混じった計算問題を解いてみましょう。
混合計算のやり方
例題3(混合計算)
逆数にするのは「÷」直後の分数だけでよいので、この問題では12だけを逆数のかけ算にします。
13÷12×15=13×21×15=1×2×13×1×5=215
215
簡単ですね!
÷の直後の分数だけを逆数にして掛け算
13÷12×15=13×21×15=
=1 x 2 x 13 x 1 x 5=215
では、練習しましょう。
問題で定着
●類題3-(1)
●類題3-(2)
●類題3-(3)
整数を○分数に直しましょう
●類題3-(4)
●類題3-(5)
●類題3-(6)
 爽茶
爽茶もっと計算問題を解きたい人は市販の問題集を使うのも良いですね。
次のステップへ
 爽茶
爽茶これで分数の計算はすべて学習しました!「分数の文章問題」
など他の記事を読みたい人は「分数の総まとめ」から見て下さい♪
この記事があなたの役に立てたなら本当にうれしいです!