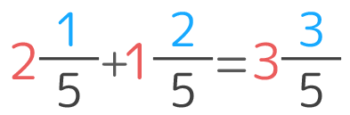「帯分数の足し算引き算、分数のくり上がり・くり下がりが分からない…」とお困りの小学４年生の方、もう大丈夫ですよ！東大卒講師歴20年の図解講師「そうちゃ」が分かりやすくまとめます。
目次(クリックでジャンプ)
(復習)分数の足し算・引き算
爽茶こんにちは！「そうちゃ」@zky_tutor(プロフィール)です。
今回は「帯分数」を使った足し算引き算を学習しますが、小3で習った「分数の足し算・引き算」を軽く思い出してください。分子だけを足し引きすればOK！分母はそのまま
例:35+15=3+15=45
例:35－15=3-15=25
爽茶(新登場)帯分数と足し算
爽茶例題を順に解いていくうちに、すぐ分かると思います。
解き方を理解♪
例題1(1)
真分数の足し算ですが、答える前にちょっと考えて下さい
分子を足すと3+4=7なので75になりますが、解答するときは帯分数に直さないとダメです。
75→125になります。125
仮分数から帯分数への直し方が分からない・忘れた人は参考記事「分数の総まとめ」内「分数の種類」を見直して下さい
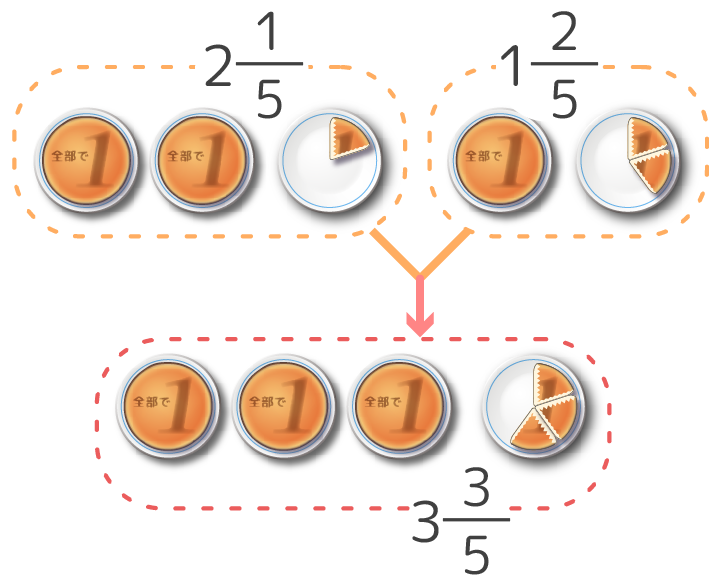
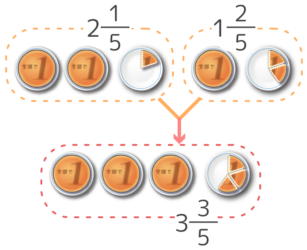
例題1(2)
帯分数の足し算は初めてですね。図で考えて見ましょう
円形(パン)の図で表すとこうなって、
335になります。335
今の計算をもう一度みると、整数部分は2+1=3、分子は1+2=3、分母は5のまま変わっていません。
整数同士、分子同士は足して、分母はそのままにすれば良いと分かりますね。
整数部分同士・分子同士を足す。分母はそのまま
このルールを使って計算をしていきましょう。
例題1(3)
答える前にちょっと考えて下さい
さっきのルール通り、整数同士・分子同士を足すと、
157+367=4117 になりますが、117は仮分数なので帯分数に直すと147になるので、元の整数部分4と足して、547になります。547
今の作業を「分数のくり上がり」と言います。
4117→ 4+117→ 4+147→ 547
爽茶分数の「くり上がり」
「分数の繰り上がり」だけを練習をします。
例題2(1)
553=6□3
分数部分が仮分数になっているのでこれを帯分数に直すとどうなりますか？(▼をクリック)
この新しく出来た整数部分の１が、もとからあった整数部分に加わって６になります。
これで、答えが出ますね。
553→5+53→5+123→623と直せるので□=2
例題2(2)
3137=4□7
分数部分137を仮分数から帯分数に直すと167になります。
この新しく出来た整数部分の１が、もとからあった整数部分3に加わって4になります。
つまり、337→ 3+137→ 3+167→ 467 と直したわけですね
□=6
例題2(3)
1=□3
似た問題を思い出しましょう
以前、同じ問題を解いたので覚えている人も多いでしょう。1=33でしたね。□=3
「分数のくり上がり」のコツが分かりましたね？では練習問題を解いて下さい！
問題で定着！
●類題2(1)
整数同士・分子同士を足し算して、375 になりますが、分数部分が仮分数になっているので帯分数に直すと75→125となります。
この横に出た1は、もともとあった整数部分の３を4に繰り上げるので、425になります。
425
●類題2(2)
整数同士・分子同士を足し算して、7119 になりますが、分数部分が仮分数になっているので帯分数に直して119→129となります。
この横に出た1は、もともとあった整数部分の7を8に繰り上げるので、829になります。
829
●類題2(3)
整数部分は0+3=3 のまま、分数部分は分子を足して5+1=6なので366 となりますが66→1なので、この1が整数部分の3を4に繰り上げます。
→ 3+66→ 3+1→ 4
4
これで帯分数の足し算は終了です。次は引き算です。
帯分数と引き算
爽茶帯分数の引き算も「普通は」整数同士・分子同士を引き算すればOKです。「普通は」の意味はすぐ分かります
とりあえず、やってみましょう♪
解き方を理解する♪
例題3(1)
ここに考えるヒントや方針
整数同士を引き算すると2-1=1、分子同士を引き算すると4-1=3 で、分母は引き算せず3そのままです。113
今の問題は「普通」に出来ました。次はどうでしょうか…
例題3(2)
整数同士を引き算すると4-2=2ですが、分子同士の引き算が2-4で出来ません…でも大丈夫です！こういう場合も分子を大きくする方法があります。
まず整数部分の4を3と1に分けます。429→4+29→3+1+29
ここで1=99を利用して分子を9よりも大きくします。3+1+29→3+99+29→3+119→3119
これで、分子を4から11に大きくできたので、もとの問題 429-249 を 3119-249 に直して、引き算が行います。
整数部分は3-2=1、分数部分は11-4=7、なので179です。179
今の作業を「分数のくり下がり」といいます。
4+29→ 3+1+29→
3+99+29→ 3+119→ 3119
分子を大きくできる♪
爽茶分数の「くり下がり」を練習
練習問題に行く前に、帯分数の「繰り下がり」だけの練習をしてみましょう。
例題4(1)
413=3□3
1=33を利用して繰り下げます。
413→4+13→3+1+13→3+33+13→3+43→334です。□＝4
例題4(2)
3=2□5
1=55を利用して繰り下げます。
3→2+1→2+55→255です。□＝5
問題で定着！
繰り下がりのコツをつかんだところで、引き算の問題をやってみましょう。
まず分子を見比べて「そのまま」計算するか「繰り下がり」をしてから計算するかを考えて下さい。
●類題4(1)
分子を見比べると、6-2 で引き算ができるので、繰り下がりは必要ありません。
分子を見比べると、6-2 で引き算ができるので、繰り下がりは必要ありません。
整数部分の引き算は3-2=1 で分数(分子)の引き算は6-2=4 なので147です。147
●類題4(2)
分子を見比べると、2-4 で引き算ができないので、繰り下がりが必要です。
分子を見比べると、2-4 で引き算ができないので、繰り下がりが必要です。
1=99を利用して
429 → 4+29→3+1+29 → 3+99+29 → 3119 繰り下げで分子を大きくできました。
これで、429-249 を 3119-249 と直して引き算ができます♪
分数部分は11-4=7整数部分は3-2=1 なので179です。179
●類題4(3)
引かれる数に分数がないので、繰り下がりが必要です。
引かれる数に分数がないので、繰り下がりが必要です。
1=66を利用して、4→3+1→3+66→366 繰り下げで分数を作ります。
これで4－56を 366－156に直して引き算ができます♪
整数部分は3-1=2、分数部分は6-5=1なので216です。216
爽茶足し算引き算の混合計算
爽茶3つの数の計算ですが、一度に計算できるのは2つだけです。落ち着いて丁寧に計算して下さい。
●混合計算(1)
●混合計算(2)
●混合計算(3)
計算順序に注意しましょう！
爽茶最後は文章題です。楽しんで解いて下さい！！
もっと計算問題を解きたい人は市販の問題集を使うのも良いですね。記事の最後にオススメの問題集があるので見て下さい。
文章問題
爽茶●文章問題-1
まずたし算か引き算か考える。
「飲む」「使う」「取る」こういうのは引き算なので、215Lー25L を計算しますが、
分子を見比べる「1-2」になっていて引き算ができないので「分数の繰り下がり」で215の分子を大きくします。
これで引き算ができます♪
215Lー25L＝165Lー25L=145L
145L[/su_spoiler]
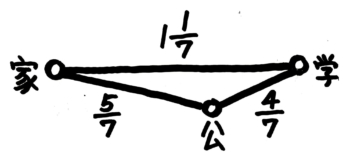
●文章問題-2
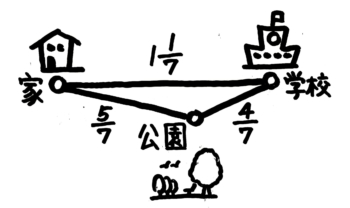
簡単な図を書くと式を作りやすい
図を書くか想像すると…
普段の道のりは117Km、今日の帰りは47Km+57Kmなので、多く歩いた分は (47+57)ー117 と分かります。
ここで大切なのは、いきなり47+57 を計算せずに、式全体を書いて計算の手順全体を頭に入れることです。
はじめの足し算は47+57 =97 になります。計算途中なので仮分数のままにしておきます。
次の引き算は 97–117 ですが、整数部分の引き算ができません(汗)
こういう場合は２つのやり方があります。
(A)97を帯分数127に直して 127–117 という計算にするか
(B)117を仮分数87にして 97–87 という計算にします。
当然、どちらも答えは17kmになります。
(A)と(B)どちらのやり方が良いかというと、計算途中は仮分数が便利ですので(B)のやり方がオススメです。
答: 17km
●文章問題-3
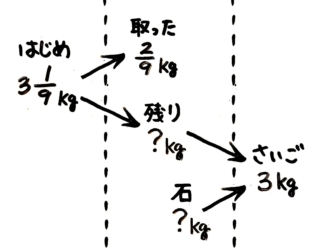
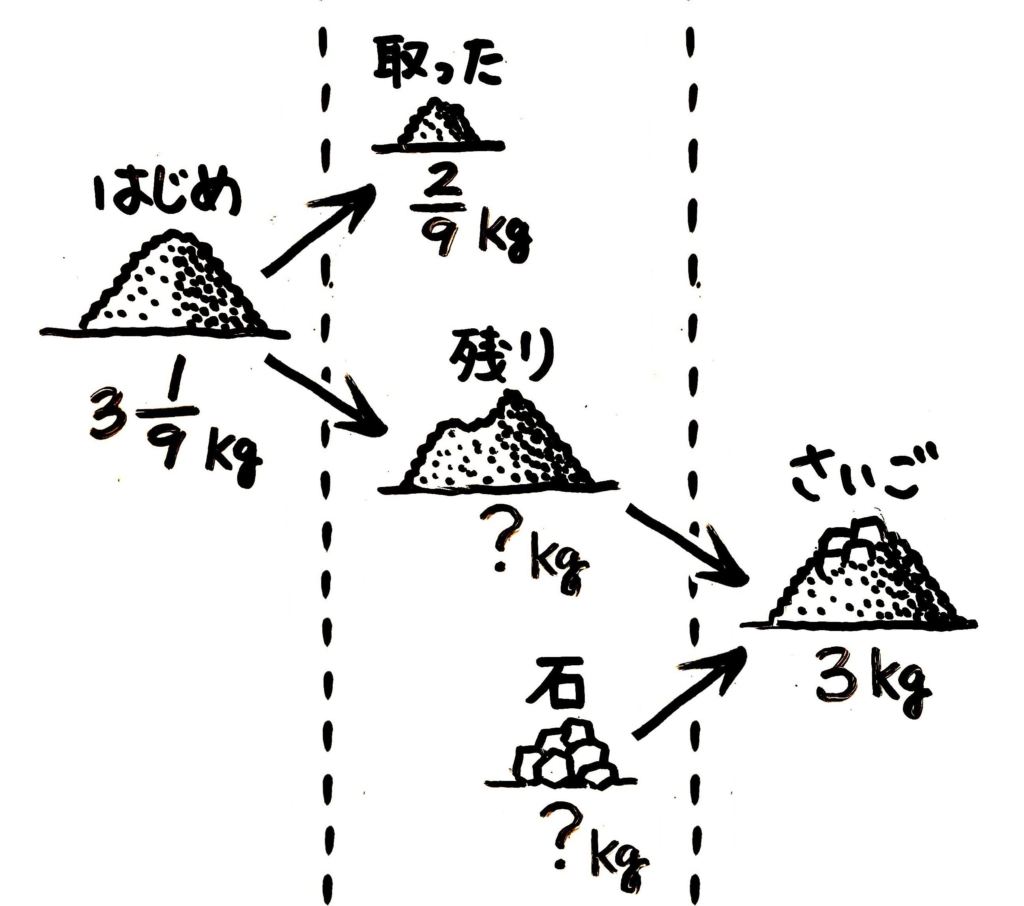
これも簡単な図を書くと良いですね。
図を書くか想像すると、
Bくんが取った残りは319Kg-29Kgなので、
Cくんがよそから運んできた石の量は、3-(319Kg-29Kg)と分かります。
小問2と同じく、これから行う計算の全体像を頭に入れてから、一つ一つの計算をするのが大切です。
まず、カッコの中の計算をすると319–29＝2109–29＝289 です。(分数の繰り下がりで319を2109に直しています。)
残りの計算は3-289 で、これも繰り下がりを使って、
3-289＝299-289 =19 です。
答: 19kg
帯分数の足し算引き算は以上です。お疲れさまでした！
この記事のまとめ
●帯分数の足し算・引き算
→整数と分子同士を足し引きする（分母はそのまま)
(例)127+237=( 357 ) (例)779－327=( 457 )
●帯分数の「くり上がり」「くり下がり」
・413→3+1+13→3+33+13→343
→分数の総合案内に戻る
おすすめ教材
爽茶オススメの問題集
●「毎日のドリル」(学研)はスマホアプリとの連携でやる気をアップできる問題集です。(くわしい案内はこちら)。
●「分数の計算(算数基礎マスター)」は3年から6年の分数計算をカバーしているので学校の予習復習はもちろん、中学受験に向けた先取り学習にも使えます。低学年のうちに買うと長く使えてオトクですよ！
「分かりやすい！」と評判の
今なら14日間無料♪この期間内に利用を停止すれば料金は一切かかりません。この機会に試してみては？