「分数をしっかり予習したい」「確実に身につけたい!」という小学3年生の方、えらいですね！
東大卒講師歴20年の図解講師「そうちゃ」が応援します。この記事で分数を得意にしちゃいましょう！
記事の最後にクイズ形式の確認テストを設置しました！目次をクリックするとジャンプできます
目次(クリックでジャンプ)
2年生で習った分数の復習
爽茶こんにちは！「そうちゃ」@zky_tutor(プロフィール)です。
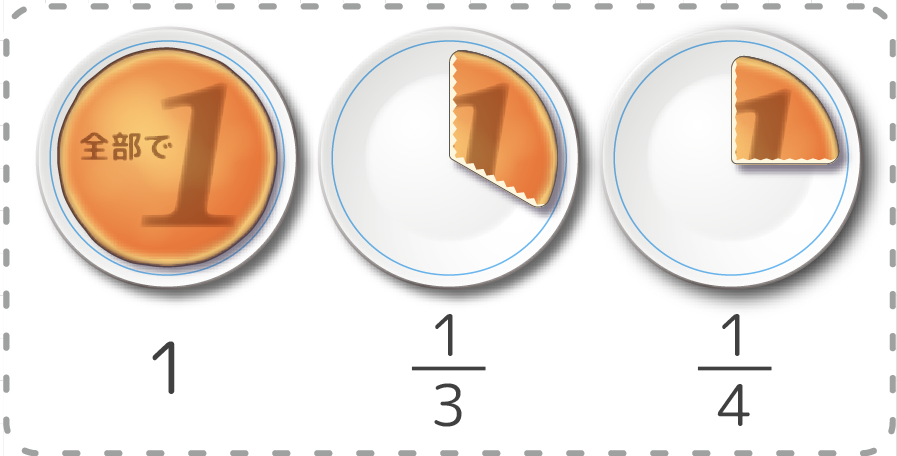
小学三年生の人は、一年ぶりの分数ですね。少し復習をしましょう♪分数は、こんな形の数でしたね！。
横線の下の数字(2)が「分母(ぶんぼ)」で上の数字(1)が「分子(ぶんし)」でした。
分母から先に読むので、この分数は
「にぶんのいち」
と読みましたね！(書くのも分母からです)
1A=(1個のモノを)
A等分したうちの1ピース
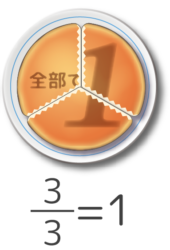
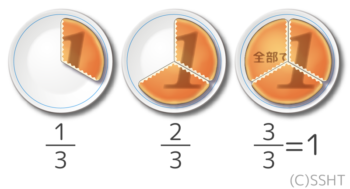
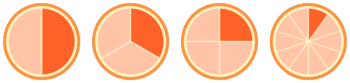
分数は「(1個のモノを)ひとしく分けたうちの1ピース」という意味でした(図1)。教科書にはありませんでしたが、分母が3や5でもOKです(図2)。
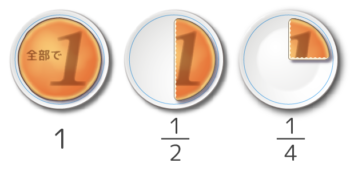
2個に分けたうちの1ピースが12(中)
4個に分けたうちの1ピースが12(右)
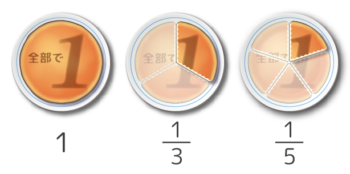
3個に分けたうちの1ピースが13(中)
5個に分けたうちの1ピースが15(右)
確認テストをしてみましょう
17はどのような大きさですか？
→( 1個のモノを7等分したうちの1ピース )
110はどのような大きさですか？
→( 1個のモノを10等分したうちの1ピース )
爽茶分子(上)を大きくする
爽茶では、分子が1から2,3…と大きくなっていくと、どうなるでしょうか？
仕組みを理解♪
●例題1-(1)
13はこうでした。これをもとに考えます
13は「(1個のモノを)等しく3個に分けたうちの1ピース」という意味でしたから、
23は「(1個のモノを)等しく3個に分けたうちの2ピース」という意味になりますね。それを図にすると…こんな風になります。
絵ではなく図にするとこうですね(答え)
答: (図を参照)
このように、分数の分子は1より大きい数にもなれるのです。
BA=(1個のモノを)
A等分したうちのBピース
(Bは1,2,3…Aまで増えても良い)
(例)13=1個のモノを
3等分したうちの1ピース
この考え方を使って続きを解いて下さい。
●例題1-(2)
33は、3つにわけたうちの3ピースなので、こんな感じです。
図にすると、こうですね(答え)。
(図を参照)
●例題1-(3)
「33」はパン丸ごと1個なので「１」と同じですね。
1と同じ
このように、
分母と分子が等しい分数は「1」と同じです。
AA=1
13から23、33 と分子が大きくなる
につれて数としても大きくなり
33は1と等しくなります。
練習問題で定着♪
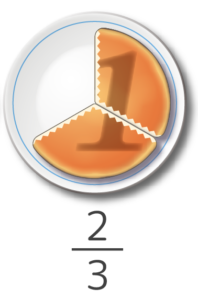
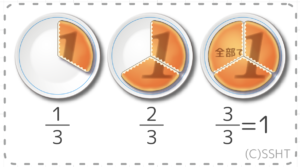
今まではパンの絵でしたが、今度は違う絵を練習します。
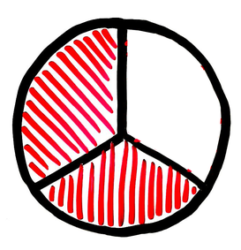
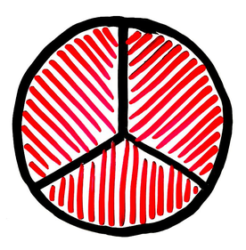
ロールケーキを上から見た図だと思って下さい(図1)。1/3は、これを三等分したうちの一つ、2/3は２つになります(図２)
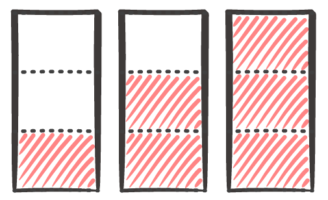
次の問題では、この長方形を使って分数を図にして下さい。
類題1(分子を大きく)
(1)14 (2)34 (3)44
●類題1-(1)
四等分したうちの1つなので、こうなりますね。
答: (図を参照)
類題1-(2)
四等分したうちの3つなので、こうなりますね。
答: (図を参照)
類題1-(3)
四等分したうちの4つなので、こうなりますね。
そして、これは長方形まるごと一つになっているので、１と同じ大きさになります。
答: (図を参照),1と同じ
分子を大きくすると分数自体も大きくなっていくのが分かりましたね？
次は、分母(下)を大きくするとどうなるか、見ていきます！(カンが良いあなたは分かっているかもしれませんね！)
分母を大きくする
爽茶では、同じ分子のまま分母(下)だけが大きくなるとどうなるか考えてみましょう！
仕組みを理解する♪
例題2(分母を大きくする)
2(1)
パンの絵を思い出しましょう
先程図に書いたので分かりますね
答:23の方が大きい
「13<23」と表します。
つまり、分子が大きくなっていくと分数全体も大きくなっていきます。
2(2)
パンの図をイメージすると…
答: 13の方が大きいですね
2(3)
間違えても良いので何か答えて(書いて)下さいね
分子が大きくなると分数は大きくなりますが、反対に
分母が大きくなると分数は小さくなります。
分数の意味(ABはB等分したうちのA個)を
思い出して、12と110を比べれば分かりますね？
110つまりパンを10等分したうちの一つなんて、ほんの少しになってしまいますよね。
(T^T)g
数量としては小さくなる
このように、分母が大きくなっていくと、分数は小さくなっていきます。
わかったことをもう一度まとめると、こうなります。
- 分子だけが大きくなると、数としても大きくなる。
- 分母だけが大きくなると、数としては小さくなる
確認テストをどうぞ♪
(1)57と27で大きいのはどちらですか？
→( 分母が同じなので分子を比べる。分子が大きい57の方が大きい )
(2)29と27で大きいのはどちらですか？
→( 分子が同じなので分母を比べる。分母が大きい27の方が大きい )
爽茶次は「数直線」の上に分数を表してみましょう。
数直線と分数
爽茶数直線の意味と書き方
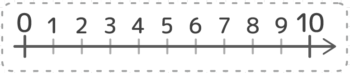
定規を使ったことがありますよね？定規には数字が書いてあって左端から1cm、2cm、3cm、4cm…と数字が大きくなっていきます。あれが数直線に近いイメージです(図)。
ゴミがついてますが、気にしないで…
図にするとこんな感じです。真っ直ぐな線(直線)の上の数字が右に行くにつれて1,2,3,4…と増えていきます。
では、分数の話に戻って、数直線で分数を表すとどうなるか分かりますか？
分数の意味をもう一度出すと、こうでしたね
BA=(1個のモノを)A等分したうちのBピース
今までは1個のパンやロールケーキを分けてきましたが、今度は1個でなく数直線の「1」までの長さを分けると考えます(図1)。
この長さを分けると考えます
では問題を解きながら理解して下さい。
数直線上に分数を表す
例題3-(1)
まず13を数直線上に表しなさい
13は等しく3つに分けたうちの1つです。
まず、数直線上に「0」と「1」を書き
「0」から「1」までの長さを三等分します。
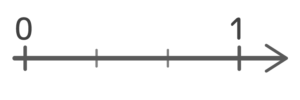
「区切り」が２つできますが「13」は最初の1つという意味なのでこうなりますね。
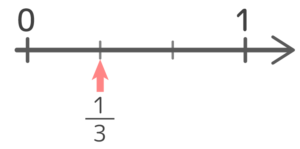
ロールケーキを切るのと似ていますよね？
このような図を書くときはフリーハンドで構いません。というか、フリーハンドで書けるようにしましょう！
三等分は難しいので、上手に三等分が出来るようになりたい人は当ブログ「線分図基礎講座」の「線分の三・九等分」を見ると良いかもしれません。
例題3-(2)
さきほどの13の長さ2つ分なので、こうなります。2つあった区切りの右の方ですね。
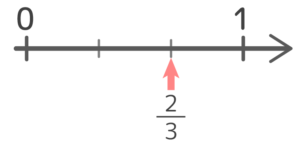
例題3-(3)
「33」という形で何か思い出しませんか？
もうお分かりですね。33＝1 です。
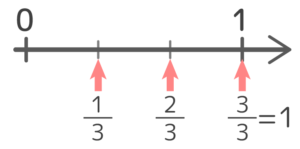
これで、数直線と分数の関係が分かりましたね♪
分数は、数直線の「0と1の間の長さ」を等分した大きさで表す事ができる。
確認テストをどうぞ♪
次の数直線を見て、アに当てはまる数を答えなさい
→( 目盛りは0から1を5等分しているので、アは15 )
──┼─┼─┼─┼─┼─┼─＞
──┼─↑─↑─↑─↑─↑─＞
──┼─ア─イ─ウ─エ─オ─＞
エに当てはまる数を答えなさい
→( 一つの目盛りが15で、エは四目盛りなので45 )
爽茶分数と小数
爽茶小数と分数の関係
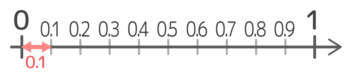
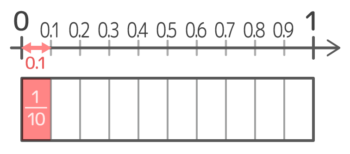
小数「0.1」は、0から1までの間を10等分したうちの一つでした。
これは110と同じ大きさですね!
つまり、0.1=110 ということです。
小数の「0.1」と分数の「110」は等しい
この性質を使って問題を解いてみましょう！
問題で練習♪
●例題4-(1)
0.3は0.1が3つ集まったものです。
0.1が110になるので、0.3は310ですね。310
できましたか？出来た人はその調子で、間違えた人も気にせずに、次の問題に挑戦して下さい。
●例題4-(2)
610は110が6個集まったものです。
110が0.1なので、610は0.6ですね。0.6
いよいよ最後の問題です。
●例題4-(3)
答えを書く前に…気をつけましょう
110が0.1なので、910は0.9です。0.8と0.9を比べると、大きいのは0.9ですね。
ただ！ココで注意です。答える時は、問題文と同じ分数の形で答えましょう！910
これで終了です。お疲れさまでした！
まとめと確認テスト
まとめ
この記事のまとめを確認テストの形式にしました。タッチする(パソコンの場合ポインタをあてる)と答えが見えます。全部理解できたかチャレンジして下さい。
● 分数の意味(小3) ●
BA=( (1個のモノを)A等分したうちのBピース )
● 分母と分子が等しい分数 ●
( 1 )と同じ。例:33=( 1 )
● 分子が大きくなると ●
数としては(大きく)なる
14( < )24( < )34
● 分母が大きくなると ●
数としては( 小さく )なる
12( > )13( > )14
● 小数と分数の関係 ●
0.1＝( 110
)
クイズ形式のテスト！
爽茶→分数の総合案内(まとめ)に戻るまた小3の方には以下の記事も合わせておすすめです。
→三角形 →正方形・長方形
おすすめ教材
爽茶●「分数の計算(算数基礎マスター)」
●「小4までに…数の思考センス(シグマベスト)」
「分かりやすい！」と評判の
今なら14日間無料♪この期間内に利用を停止すれば料金は一切かかりません。この機会に試してみては？