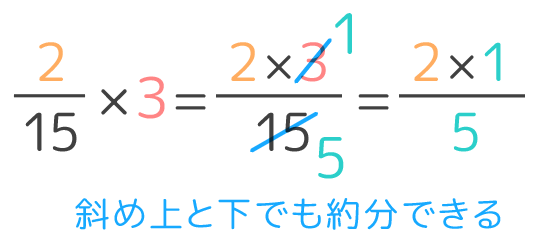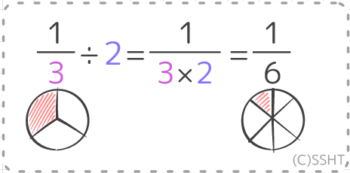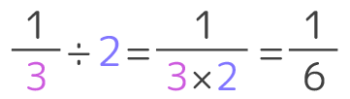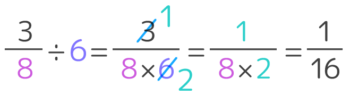「分数と整数の割り算」を予習・復習したい小5の方へ。
講師歴20年の図解講師「そうちゃ」が分かりやすく説明します。
記事を読んで真似すれば「分数÷整数」のルールをしっかり身につけられますよ
目次(クリックでジャンプ)
分数÷整数の計算方法
計算方法を理解
例題3(分数と整数のわり算)
分け方が変わります
毎回登場する図で、13は三等分したうちの1ピースです(図1)。そして、13÷2は今の1ピースを半分にします(図2)。
1ピースの半分になる
三等分だった分け方が2倍になり,そのうちの1ピースなので、六等分したうちの1ピース、つまり16 になります。16
さて、今の計算式をもう一度見るとこうなっています。
さっきのパンの図を思い出すと、三等分だったのが二倍の六等分になっていたので、分母の6は 3×2=6 だと分かります。つまりこういう計算をしたことになります。
この式を見れば、分数を整数で割る場合、分母×整数をすれば良いと分かります
分母に整数をかければ良い
実際の解き方・教え方
「分数のわり算は結局はかけ算」「だから簡単だよ」と謎理論で(汗)生徒の苦手意識をとにかく軽減してあげましょう。
その上で「かけ算は分子にかけたけど、わり算は分母にかける」と対比すると、生徒の頭に焼き付きます。
かけ算の時と同じように❶準備→❷かけ算という2ステップで行わせます。
では、類題で練習しましょう！公式通りに計算すれば大丈夫ですよ！
分数÷整数の練習問題
●類題3(1)
公式通り、分母に整数をかけましょう。
公式にあてはめて、分母と整数をかけます。
25÷3=25×3=215 です。215
●類題3(2)
計算する時は◯分数
掛け算の時と同じく、帯分数は仮分数に直してから計算します。
257=2×7+57＝197 ですから、257÷5=197÷5=197×5=1935です。 1935
●類題3(3)
答える時は◯分数
掛け算の時と同じく、帯分数は仮分数に直してから計算します。
279=2×9+79＝259 なので、279÷2=259÷2=259×2=2518 になりますが、仮分数は、答えを書く時は帯分数に直します。
2518⇒1718 になります。1718
仮分数から帯分数の直し方を復習したい人は参考記事「分数のまとめ」内「分数の種類」を見直して下さい。
●類題3(4)
途中でかけ算と同じような工夫ができます。
38÷6＝38×6 ここで、分母の6と分子の3を通分します。
38×6 ⇒18×2=116 です。116
「分数÷整数」のルールをもう一度まとめるとこうなります。
❶分母に整数をかける
❷計算するときは仮分数にする
❸計算途中で約分をしてもよい
❹答えるときは帯分数にする
実際の解き方・教え方
途中の約分を入れると3ステップで解かせることになります。
❶準備
等号と長い横線を書いて問題文の数値を「移す」。整数は分母に
❷約分
約分できないか調べさせて約分させる
❸かけ算
分母でかけ算をして答える
とにかく分数については絶対に苦手意識を持たせたくありませんので、最初はゆっくりで良いのでステップごとに確実に計算を身に着けさせることが大事です。
爽茶分数・整数の割り算とかけ算
爽茶混合計算で気をつけるのは
◉割り算は分母にかける
これだけです。気楽に♪計算しましょう。
◆混合計算-1
「かけ算は分子に、割り算は分母にかける」ですよ
◆混合計算-2
●分数は○分数に直しましょう
◆混合計算-3
たくさんの数がありますが、やり方は同じです。
次は、アレ？と思うかもしれません(汗)
◆混合計算-4
分数の意味(●■=●÷■)を思い出しましょう
最後の(4)で分かるように、整数の割り算は分数計算にすると約分が出来て計算がとても楽になります。
これからは、このように解きましょう♪
次のステップへ
爽茶「分数の総合案内」から「分数と分数のかけ算わり算」を予習しておきましょう