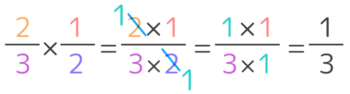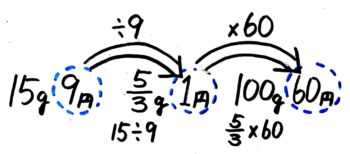
「分数のかけ算と割り算の文章問題を解きたい!」という小学6年生の方、まかせてください!
東大卒講師歴20年の図解講師「そうちゃ」が分かりやすく教えますよ♪
これを読めば文章問題で迷うこともなくなる!かもしれませんよ
目次(クリックでジャンプ)
分数のかけ算・割り算(確認)
 爽茶
爽茶こんにちは!「そうちゃ」@zky_tutor(プロフィール)です。
文章題を解く前に、ちょっとだけ確認します。「分数×分数」「分数÷分数」で学習したルールを確認すると、かけ算はそのまま、割り算はひっくり返してかけ算でした。
❶分子同士・分母同士をかければ良い
❷整数と帯分数は仮分数に直して計算
❸計算途中で約分をしてもよい
❹答えるときは帯分数に直す
わり算は「÷」の直後の分数の上下を逆さま(逆数)にしてから、かけ算。
分子分母をひっくり返してわり算をかけ算にする

思い出したところで、文章問題に行きましょう。
分数の文章問題の解き方
 爽茶
爽茶文章題-(1)図形v
「長方形の面積=縦×横」でした
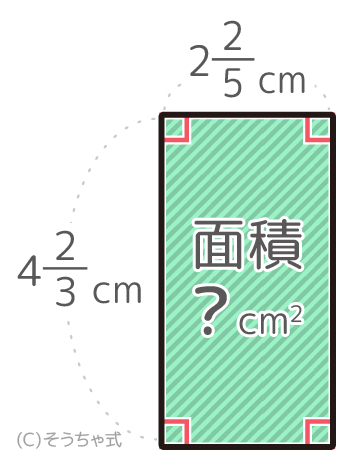
公式通りに式を立てて計算すると、423×225=143×125=14×123×5=14×41×5=565=1115 と分かります。
1115cm2
文章題-(2)単位v
長さが2倍になれば重さも2倍、長さが3倍になれば重さも3倍です。
長さが123mということは、長さが1mの123倍になっているので、重さも45kgの123倍になるということです。
このような「単位あたりの量」は「二重の矢印図」を書きます。詳しくは当ブログの記事「割合のまとめ」内の「単位あたりの量」を見て下さい。
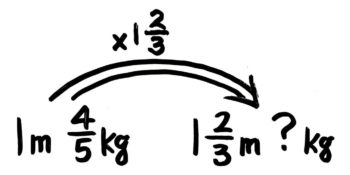
図を見るかイメージすれば、?=45×123と分かるので、これを計算して、
45×123=45×53=4×55×3=4×11×3=43=113
です。113kg[/su_spoiler]
文章題-(2.5)単位v
ペンキの量が2倍になれば塗れる広さ(面積)も2倍、ペンキの量が3倍になれば重さも広さ(面積)も3倍です。
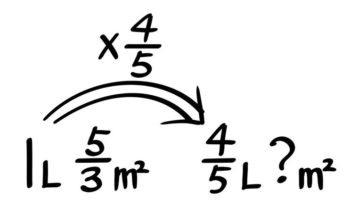
ペンキの量が45Lつまり1Lの45倍になっているので、塗れる広さも53m2の45倍になるということです。
第2問と同じように「二重の矢印図」を書くとこうなります。

「ペンキの量」も「塗れる広さ」も同じだけ倍される
図を見るかイメージすれば、?=53×45と分かるので、これを計算して、
53×45=5 × 43 × 5=1 × 43 × 1=43=113
です。113m2[/su_spoiler]
文章題-(3)図形v
「台形の面積=(上底+下底)×高さ÷2」でした
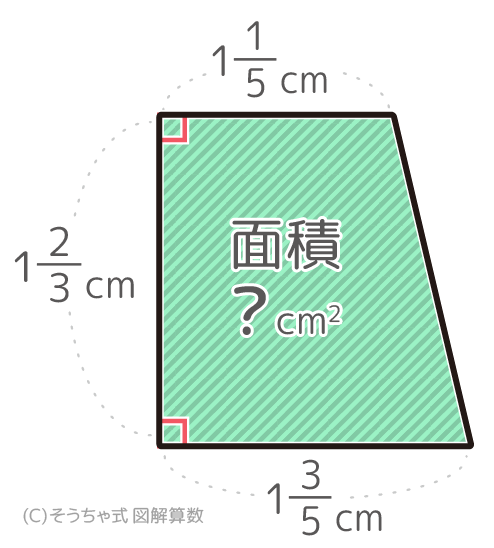

台形の面積の公式通りに式を作って計算して
(65+135)×123÷2=(65+85)×53×12=145×53×12=14×5×15×3×2=7×1×11×3×1=73=213です。213cm2
文章題-(4)割合v
「225mが全体の47にあたる」は「全体×47=225m」と同じ意味でした。当サイトの参考記事「割合まとめ」内の「」を参考にして下さい。
「全体×47=225m」なので、割合の矢印図を書くとこうなります。
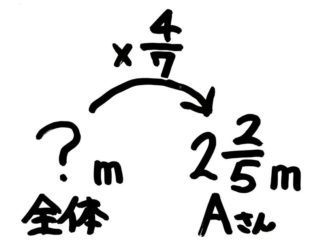
反対向きの矢印は割り算になるので「?=225÷47」と分かります。
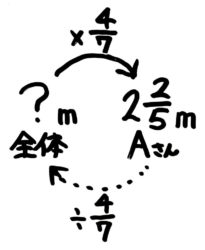
「?=225÷47」と分かります
これを計算して、225÷47=125×74=12×75×4=215=415です。415m
次の問題は少しむずかしいかもしれません。
文章題-(5)図形v
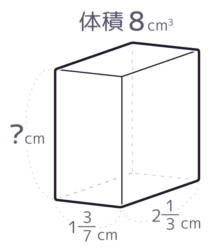
公式「直方体の体積=縦×横×高さ」を使って、分からない数を□にして、とりあえず式を立ててみましょう。
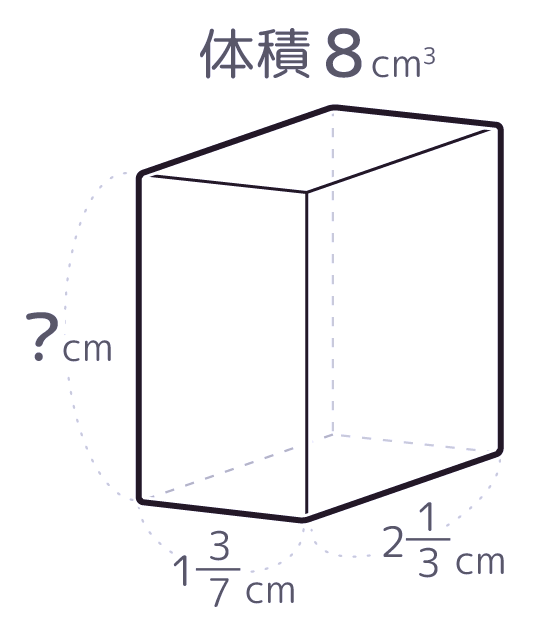
分からない数である高さを□にして、式を立てるとこうなります。
213×137×□=8
この式を計算できるところまで計算します。
213×137×□=8 →(73×107)×□=8 →(103)×□=8
「103×□=8」この逆算を解くには、同じ形の「2×3=6」を参考にして、真ん中の数=右の数÷左の数 と分かります。(くわしくは参考記事「逆算のまとめ」を見て下さい。)
→□=8÷103=8×310=2410=125=225
225cm2
文章題-(6)割合
あまり難しく考えずに式を立てて下さい♪
割合を学んだときの矢印図を二段つなげて図を書くとこうなります。
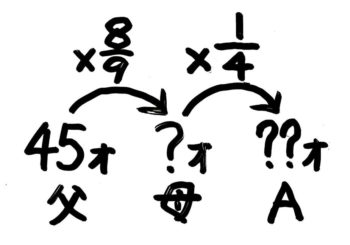
Aは45×89×14と分かります。
A君(図の「??」)はお父さんの89の14なので、45×89×14才です。
これを計算して、45×89×14=45×8×11×9×4=5×2×11×1×1=10才と分かります。10才
[/su_spoiler]
文章題-(7)割合
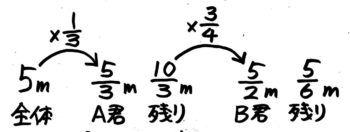
一気に答えを出そうとせずに、A君が取った分、その残り、B君が取った分、最後の残り、と一つづつ答えを出していきましょう。
A君は5mの13つまり5×13=53mを切り取ります(計算の途中では仮分数のままにしておきます)
残りは5ー53=153ー53=103m(これも仮分数のまま)。
B君はこの残り103mの34つまり103×34=10×33×4=5×11×2=52mをとります(仮分数のまま)。
5mのリボンから、A君は53m、B君は52mを切り取ったので、残りは5-53–52=306–106–156=56mです。56m
はじめにA君がリボンの13を切り取った時に、残りは1-13=全体(5m)の23と=5×23mと考えます。
次にB君が残りの34を切り取ると、最後に残るのはA君がとった残り(5×23m)の14=5×23×14と考えます。
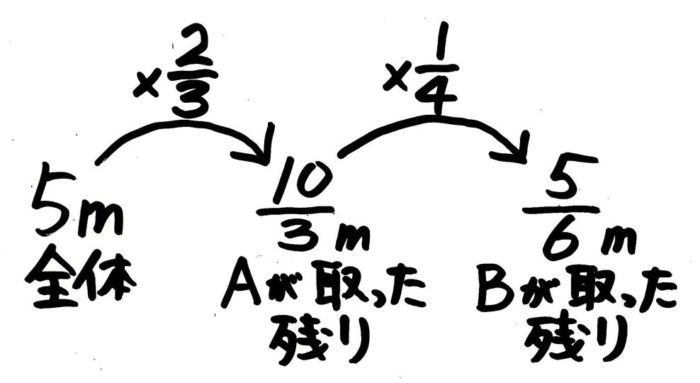
これを計算すると、5×23×14=5×2×11×3×4=5×1×11×3×2=56mと同じ答えが出ます。引き算をせずにかけ算だけで答えが出るのが便利です。
文章題-(8)単位
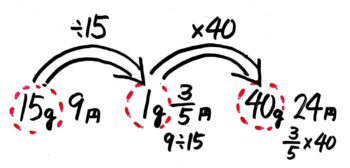
まず1gの値段を出してしまうと簡単です。
15gの値段が9円なので、1gの値段は9÷15=915=35円と分かります。
したがって、40gの値段は35×40=3×405×1=3×81×1=24円です。24円
文章題-(9)単位
同じ砂糖ですが、今度は1円あたりの重さを出してみましょう。
(8)は「gの…」と聞かれていたので「g」を÷×しましたが、この問題は「円…」と聞かれているので「円」を÷×します。
15gの値段が9円のなので、1円あたりの重さは15÷9=159=53gと分かります。
よって60円分の重さは53×60=5×603×1=5×201×1=100gです。100g
 爽茶
爽茶これで文章題も終了です。
もっと文章題を解きたい人は市販の問題集を使うのも良いでしょう。
「毎日のドリル」シリーズは各学年用に「文章題」があり、易しめの文章題が多くて文章題が苦手な生徒さんにも取り組みやすいです。
次のステップへ
 爽茶
爽茶文章問題に自信がつきましたか?
他にも分数の記事があるので「分数の総合案内(総まとめ)」から見て下さい♪
この記事があなたの役に立てたなら嬉しいです!