「通分のやり方を忘れた」という小学5・6年生の方、ご安心下さい♪東大卒講師歴20年の図解講師「そうちゃ」が通分のやり方を分かりやすく教えます!練習問題でしっかり定着も図れますよ!
目次(クリックでジャンプ)
分母をそろえる「通分」
 爽茶
爽茶こんにちは!「そうちゃ」@zky_tutor(プロフィール)です。
小3・4で「分数の足し算・引き算」を勉強した時に、分母が違う分数は足し算引き算が「できない」と教わりました。15+35=35
12+13=???
ところが!今回学習するワザ「通分(つうぶん)」を使うと違う分母を同じにして計算することができますよ!
通分のやり方を理解♪
通分には前回学んだ「分数の倍分(分母と分子に同じ数をかけること)」を使います。
こちらの誘導にのって例題を解きながら「通分」の意味を理解してください。
●例題1-1
●例題1-2
●例題1-3
上で作った分数を並べて比べてみます
| 分数\倍分 | 分母分子2倍 | 分母分子3倍 | … |
| 12 | 24 | 36 | |
| 13 | 26 | 39 |
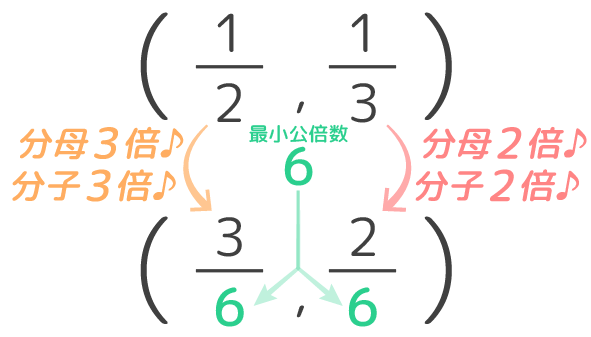
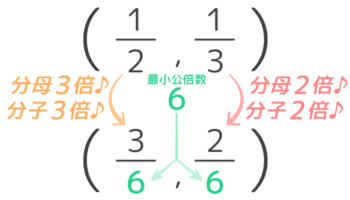
12は分母・分子を3倍、13は分母/分子を2倍した時に、分母が「6」でそろっていますね。
6
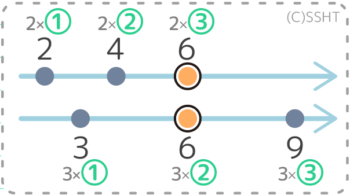
では、そろった分母は元の分母「2」と「3」とどういう関係にあるでしょうか?
このように、通分は「分母を最小公倍数にそろえる事」とも言えるのですね。
公倍数や最小公倍数を忘れた・知らない人は「公倍数の求め方」を見て下さい。また「倍数の見分け方(上)」「倍数の見分け方(下)」も参考になると思います。
 爽茶
爽茶でも実際に通分をすると結構間違える生徒さんが多いです。そこで実際の作業手順を見て下さい。
実際の作業手順(教え方)
全部で3ステップです。
◎ステップ1
2つの分数の分母を見て最小公倍数を出します。
大きい方の分母を2倍・3倍していって小さい方の分子の倍数にもなったら、それが最小公倍数です。
はじめのうちは、分かるようにはっきりメモしておくのが良いでしょう。ただし、計算は別の場所でやります。ごちゃごちゃにならいないように
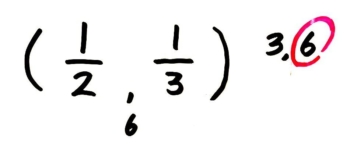
◎ステップ2(重要!)
ステップ1で出した数を分母に、分子は空っぽの分数を2つ書いて「この数に通分するぞ」と頭と体にスイッチを入れます。このステップを抜かしていきなりステップ3にいくとミスが生まれます。
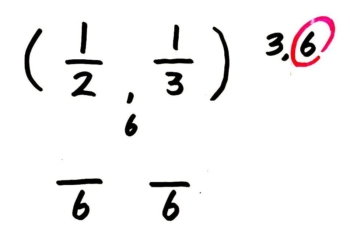
「6に通分するぞ!」
◎ステップ3
通分を1つづつ実行します。直す前の分母→直した後の分母と指でたどって、分母が何倍になっているかを「●倍」と唱えます(小さい声か、頭の中で)。
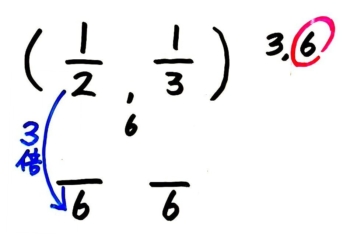
次に分子を指でたどりながら「●倍」と唱えながら分子を●倍した答えを書きます。
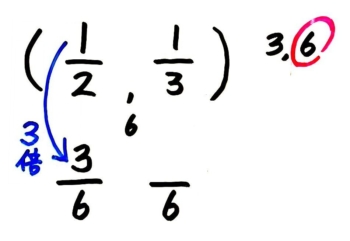
もう一つの分数も、分母を「2倍」と唱えてから

分子も「2倍」と唱えて(ながら)計算します

こんな感じで、お子さん・生徒さんに「●倍、●倍」「◎倍、◎倍」と唱えさせるとミスが無くなると思いますよ!
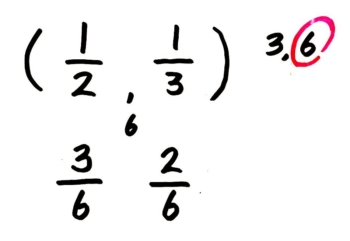
次は色々な通分のやり方を練習しましょう!
通分を練習!
●類題1-1
まず最小公倍数を求めましょう
分母が3と4なので、3と4の最小公倍数を求めます(▼をクリック)
大きい方の4を2倍,3倍していき、最初に3の倍数になるのが最小公倍数です。
4の2倍は8で3の倍数ではありません(ダメ)。
4の3倍は12で3の倍数にもなっている(OK!!)ので、最小公倍数は12です。
これで分母を12にそろえれば良いと分かります。
では、それぞれを倍分して、分母をそろえて下さい。
812,312
次の問題も、同じように解いて下さい。
●類題1-2
●類題1-3
2つの分母が特殊な関係にあります
整数との通分
●類題1-4
まず整数を●数にします。
「2」が分数ではないので、分数になおします。整数を分数に直す方法を覚えていますか?
あとは今までと同じく通分します。
このように、片方が整数の場合は、整数の分母に1をつけて分数にしてから、分数の方に合わせます。
整数Nを分数と通分したい場合、分母に1をつけて分数→N1にしてから、分数の方に合わせる
帯分数の通分
●類題1-5
帯分数の性質を考えましょう
このように、帯分数の通分は分数部分のみ通分を行います。
帯分数のまま、分数部分のみを通分する。
●類題1-6
もう一度通分のルールをまとめます。
- 通分~分母を(最小公倍数に)そろえる事
(例)12と13とを通分
→分母を2と3の最小公倍数6にそろえる
・12→(分母分子を3倍)→36
・13→(分母分子を2倍)→26
- 整数の通分
→分母に1をつけて分数(N1)にしてから、分数の方に合わせる - 帯分数の通分
→帯分数のまま、分数部分のみを通分する
 爽茶
爽茶これで通分が出来るようになりました!
次は3つの数を通分してみましょう。
3つの分数の通分
 爽茶
爽茶…少し面倒くさいだけです。
三つの数の通分のやり方!
例題2(3つの分数の通分)
分母が2,3,5なので、一番大きい5を2倍・3倍していき、2の倍数でもあり3の倍数でもあるような数が出てきたら最小公倍数です。
5の2倍は10(3の倍数ではない),3倍は15(2の倍数ではない),4倍は20(3の倍数ではない),5倍は25(2の倍数ではない),6倍は30でやっと2と3の倍数です。
つまり最小公倍数は30なので分母を30にそろえます。
12→(分母分子15倍)→1530、13→(分母分子10倍)→1030 、15→(分母分子6倍)→630 になります。
1530,1030,630
面倒くさいですが、やり方は2つのときと変わりませんね?類題で練習しましょう。
練習問題で定着♪
●類題2-1
●類題2-2
●類題2-3
 爽茶
爽茶次のステップへ♪
 爽茶
爽茶通分は分かりましたね?これで分数を好きな形に変形できるようになりました。
「分母が異なる分数の足し算引き算」へ進んで下さい。
他にも分数の記事があるので「分数の総合案内」から見て下さい!