「割合が分からない…」という小学生の方は教科書の「割合の三公式」等をがんばって覚えよう使おうと思っていませんか?そういう勉強方法は「割合」を余計に難しくしてしまいます!
実は教科書の「割合」は難しく説明しすぎているのです。もっとシンプルに「割合=かけ算」と考えれば簡単になるんですよ!
この記事では、東大卒講師歴20年の図解講師「そうちゃ」が分かりやすい考え方と図の書き方を使った問題の解き方を教えます。
記事を読んで真似するだけで割合はもう大丈夫。「何だ…それでいいの?」と拍子抜けするでしょう。
無料プリント「そうちゃ式 復プリ」をダウンロード・印刷して復習すればテストでもパッと答えられるでしょう♪
「目次」で読みたいところをクリック(タッチ)すると一気にジャンプできます。
目次(クリックでジャンプ)
要するに、
割合=「○倍」です
 爽茶
爽茶こんにちは!「そうちゃ」@zky_tutor(プロフィール)です。
割合は難しくありません!実際、皆さん普段から使っていますよ。
割合は難しくない!
思いっきり簡単にして言うと「割合」とは、あるモノが別のモノの「何倍」かを表した数です。
普段から使っている「2倍」「半分」という言葉をつかっていませんか?
これらは全部「割合」です。
→あるモノが別のモノの「何倍」かを表した数
「半分」なら「0.5倍」というのが割合になります。
つまり「割合」と言っても小2で習った「かけ算」とあまり変わらないのです。難しく考えるのはやめましょう!
「くもわ」より「●●図」!
まず「図」を書く
問題文からいきなり「式」を作るのは難しいので「簡単な図」を書いて「式」を立てますが、学校で習う「くもわ図」は…分かりづらい!!(「く」って何?「も」って何?)

「くもわ」ってコレ↑を連想してしまうよね?w
そこで、当ブログでは簡単で使いやすい「矢印図」をオススメします。
かけ算の図から
さっき言った通り「割合はかけ算と同じ」なので、まず「かけ算」の図をかいてみましょう。
例えば「妹は鉛筆を3本持っていて姉は妹の4倍持っている。姉は何本持っているか?」だと、こういう図になります。
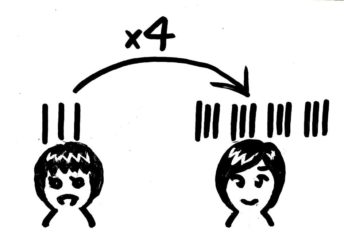
姉は妹の4倍を持っている」
この絵を文字に変えるとこうなります。
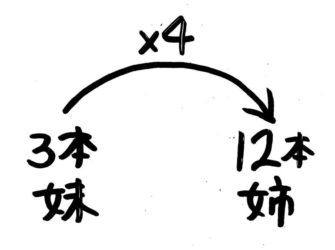
姉は妹の4倍を持っている」
これが「矢印図」です。同じ書き方で「2の3倍は6」という割合の文を書くと、こうなります。
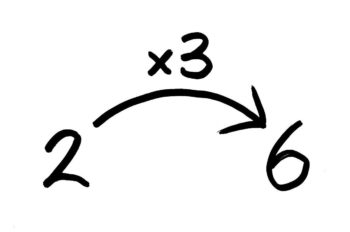
矢印の方向に沿って文字を追っていくと「2×3は6(つまり、2の3倍は6)」と読めるのが特長です。
三つの数
矢印図には「2」「3」「6」三つの数が書いてあります。分かりやすいように、それぞれに名前を付けます。
- 「2」は矢印の根本にあるので「元(もと)の数」
- 「6」は矢印の先にあるので「先(さき)の数」
- 「3」は矢印についているので「矢の数」とします。「割合」は矢の数のことです。
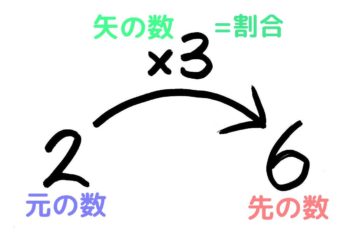
この「2×3=6の矢印図(236の図)」を覚えるだけで「割合」の問題を解くのは本当に簡単になりますよ!
矢印図を書いてみる
せっかく矢印図を紹介したので「矢印図」を作る練習をしてみましょう
●例題1-(1)
まず、数字が入るスペースは空っぽのまま「矢印図」を書いてしまいます。
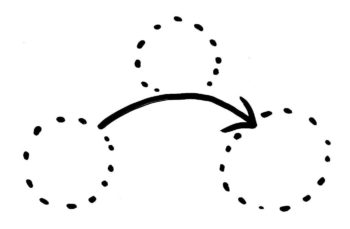
この3つのスペースに「5」「4」「20」を入れれば完成です。
まず「4」は「倍」がついているので「矢の数」と分かります。
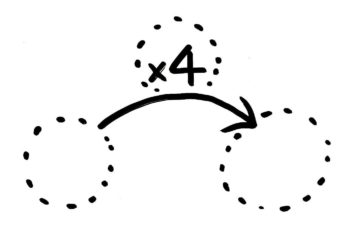
次に「5」と「20」を矢印の向きに「5を4倍すると20」と読めるようにスペースに入れると、こうなりますね?
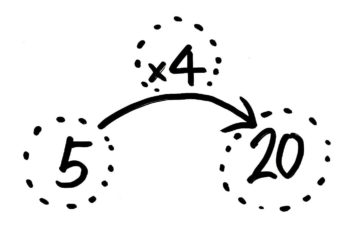
要するに、「5×4=20」という式が出来る時に、矢印の方向に「5(もとの数)」「4(矢の数)」「20(さきの数)」の順に並べれば良いのです。簡単でしょう?
→3つの数が「A×B=C」の関係にある時に、
矢印の向きに沿って「A」「B」「C」を並べた図

もう一問練習しましょう♪
●例題1-(2)
例1と日本語が少し違いますが、例1「2の3倍は6」と同じような日本語にすると「3の5倍は15」ですね。あとは例1と同じです。
「3を5倍すると15」なので「3×5=15」です。この順番に矢印にそって並べるとこうなります。
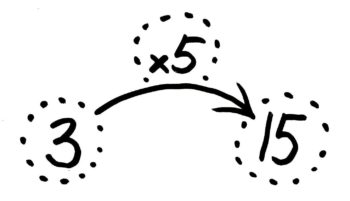
もしかしたら反対に入れてしまった人もいるかもしれませんが
図をもう一度見て「あれ?変だな」と気づくことができれば全く問題ありません!正しく書き直して下さい。
もう慣れたのではないでしょうか?次は整数以外を使います♪
●例題1-(3)
「●倍」という日本語がありません…が「半分」は0.5倍という意味なので「×0.5」と同じです。
よくやるミスはこうです。まあ、今日はじめて教わったんだからしょうがないです。ドンマイドンマイ
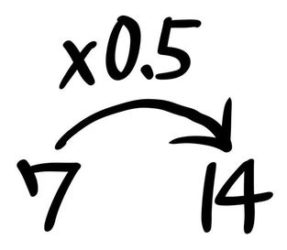
つい「小→大」にしてしまいます
今までは「もとの数」が小さく「さきの数」が大きい図、つまり「小→大」という図ばかりでしたが、そうとは限りません。
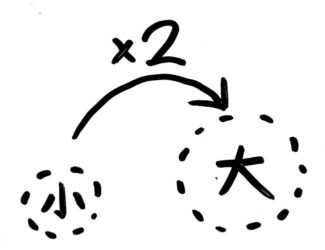
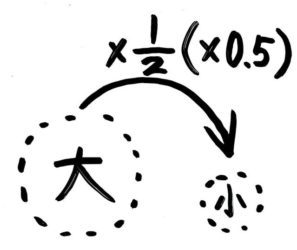
問題文「7は14の半分」を最初の「2の3倍は6」と同じような順番にすると「14の0.5倍は7」で、これを式にすると「14×0.5=7」です。
つまり数字を「14」「0.5」「7」の順に並べればOKです。
1より小さい数をかける時は矢印図が「大→小」になります。
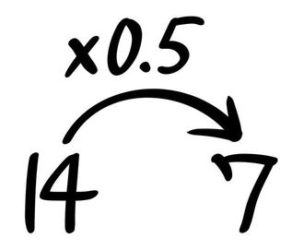
12倍なので「大→小」になります
元の数と先の数の大小をまとめると、こうなります。
①矢の数(割合)が1より大きい時
→「小→大」になる

②矢の数(割合)が1より小さい時
→「大→小」になる

 爽茶
爽茶これで「矢印図」の書き方は分かったと思います。
「矢の数」は小数にもなるので、小数の計算が苦手な人は復習しておきましょう!! →小数のまとめ
次は矢印図を使って問題を解いてみましょう!
割合の基礎問題(小5)
 爽茶
爽茶さっそく問題を解いてみましょう!
三つの数の関係
割合の問題は、三つの数のうち分からない一つの数を、分かっている二つの数の計算から出す「クイズ」のようなものです!(いやマジで)
そこで「2×3=6の矢印図」を使って、分からない数「?」を分かっている残りの2つの数で計算式を作って出す練習をしてみます。
●例題2-(1)

これは一番簡単なパターンですね。矢印の順番に読むと2×3=「?」で「?」=6ですね。
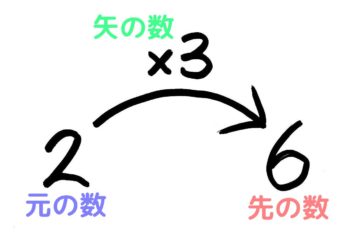
?=2×3
つまり
「先の数」=「もとの数」×「矢の数」
ということです。
二番目は「ほんのちょっと」頭を使います。
●例題2-(2)

真ん中(矢の数)が分からない場合です。
ここでは答えは分かっている(?=3)ので、6と2でどういう計算式を作れば3が出るかを考えます。

どうやって求めれば良い?
「割合はかけ算」ですが、2と6のかけ算では3は出ません…
ところで「割合」という字を見ると…
「割」という字が入っていますね!
そこで2と6の割り算を考えてみると、6÷2で3が出ますね♪
?=6÷2
つまり
「矢の数」=「さきの数」÷「もとの数」
ということですね!
最後は「矢印図」をバージョンアップします!
●例題2-(3)

このタイプが一番面倒くさいです…が、ある工夫をすればパッと分かります♪

「反対向きの矢印」を書きましょう!

反対向きの矢印は、計算も逆になる
この矢印は反対向きなので「矢の数」もかけ算と逆の割り算になります。これが矢印図のバージョンアップ!完成形です。
この反対向きの矢に沿って数を読むと「6÷3=?」となり、?=2と分かります
?=6÷3
これで
「もとの数」=「さきの数」÷「矢の数」
で出せると分かりました。
以上で、矢印図の三つの数の関係が分かりました。まとめると下のようになります。
●矢印図
3つの数が「A×B=C」の関係にある時
矢印の向きに沿ってA,B,Cを並べた図
「B(矢の数)」が割合を示している

「2の3倍は6」
「6は2の3倍」

●矢印図による割合の公式
➊さきの数(6)=もとの数(2)×矢の数(3)
❷矢の数(3)=さきの数(6)÷もとの数(2)
❸もとの数(2)=さきの数(6)÷矢の数(3)
発展形(逆向きの矢印)を書けば➊さきの数と➌もとの数は簡単に分かりますね。
❷矢の数=さきの数(6)÷もとの数(2)だけは覚えても良いですが、実は覚えなくても平気です♪(理由は、この後分かります)
問題の解き方
では、問題を解いてみます。気楽にやってみましょう♪
●例題3-(1)
これは簡単ですね。聞かれている数を「?」とすると「14の7倍は?になる」で「14×7=?」なのでかけ算をして98と分かりますね。
98
図にするとこうなりますが、図を書く前に分かる人が多いでしょう。
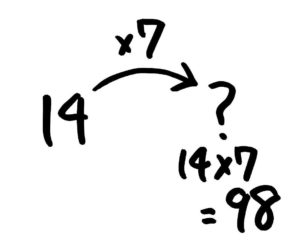
次も簡単かもしれませんね。
●例題3-(2)
問題文を「2の3倍は6」と同じ形「23の4倍は□」に直せば簡単ですね。23×4=□なので□は92と分かります。
92
図にするとこうなります。
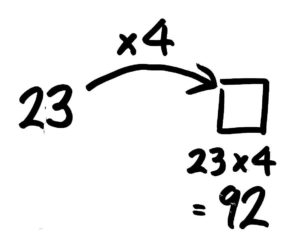
ここから少し考えましょう。
●例題3-(3)
反射的に「90÷18=5」とやってはいけませんよ!
なれるまでは、まず図を考えましょう。18と90を左右どちらにするかで、2通りの図が考えられますが…どちらの図が正しいでしょうか?
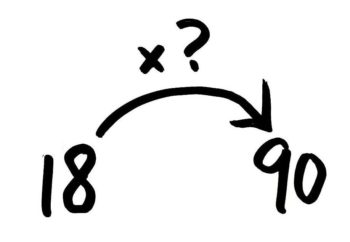
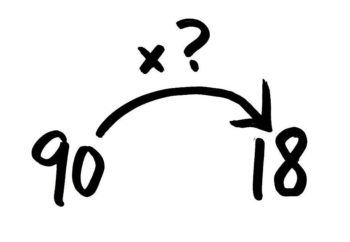
問題文「18は90の何倍か」を「2の3倍は6」と同じ形にすると「90の?倍は18」「90×?=18」になるので…正しいのはこちらです。
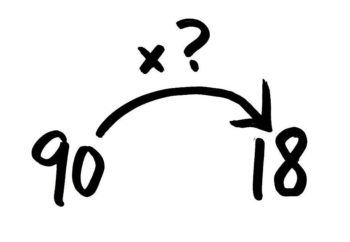
次に?(矢の数ですね)を出しますが、公式を思いつかなくても大丈夫です!となりに「2×3=6」を書いて比べてみます。
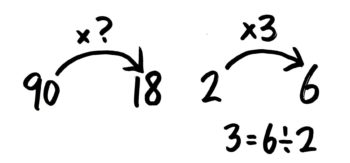
「2×3=6」を見れば、「矢の数3」は「先の数6」÷「元の数2」で出ると分かります。同じことをやれば良いので、?は18÷90で出せば良いと分かります。
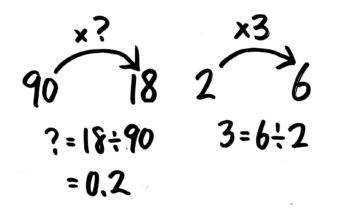
あとは落ち着いて18÷90を筆算して0.2と分かります。
0.2
このように、割合の問題でパッと答えが出ない場合は問題の矢印図と「2×3=6」の矢印図を並べて書いてみましょう。自然と計算方法が分かると思います。
公式を暗記するよりも、このやり方を勧めます。
横に「2×3=6」の矢印図を書いて、
それを見ながら計算方法を考える。
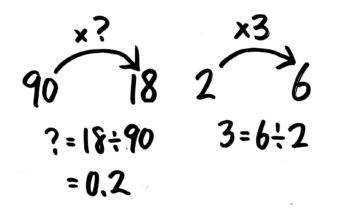
ところで、生徒さんが間違った図を書いてしまうのは、割合に慣れていないからだけではありません。
「『小÷大』という計算、つまり小数が答えになる割り算をしたくない…」というのが理由のことが多いのです。
そうならないように、小数の計算を練習させて苦手意識をなくしておくのが大切です。→小数のまとめ
次は…想像できますね?
●例題3-(4)
いつものように、文を「2×3=6」の形にするところからスタートです。
聞かれている数を「?」にすると「?×25=200」という式が作れるので、図にするとこうなります。
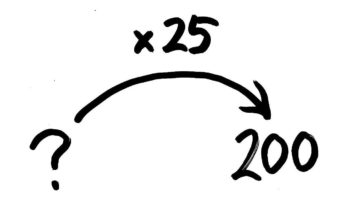
「もとの数」を出すには、逆向きの矢印を書くとわかりやすかったですね!
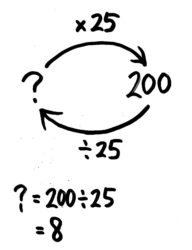
これで?は200÷25で8と分かります。
8
または、となりに「236」の矢印図を書いて、2=6÷3 と同じ計算をする、でも良いですね。
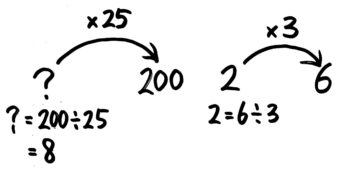
元の数=先の数÷矢の数と分かります。
ここからは、もう少し「割合の問題」っぽくなりますが、同じ様に解けば大丈夫!
●例題3-(6)
間違えても良いので、とりあえず矢印図を書いてみましょう。
「~にあたる」というのは「~倍」と同じ意味です。ですから「90は□の0.6にあたる」は「90は□の0.6倍」と同じ意味です。
これをいつもと同じ形に直すと「□の0.6倍は90」「□×0.6=90」になるので、矢印図も書けますね。
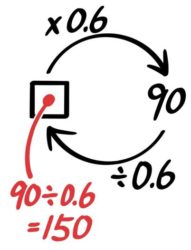
□は元の数なので90÷0.6=150
150
●例題3-(7)
「もとにしたとき」の意味がよく分かりませんが…とりあえず矢印図を書きます。

そして問題文の数のうち割合を聞かれているので「矢の数」が「?」で、「20人」は「もと」と言われているので矢印図でも「元の数」になるので、「6」は残った「先の数」と考えて図を書くとこうなります
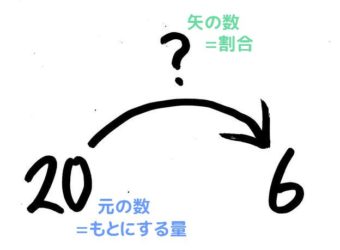
「矢の数」を出すので、公式を覚えていればもちろん、覚えていなくても「236の図」を横に書けば「矢=先÷元」と分かります。
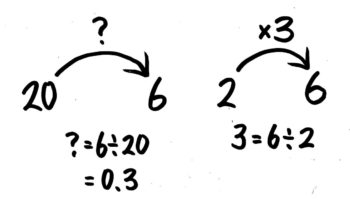
あとは6÷20を計算して0.3が答えと分かります。
0.3倍
このように「もとにする」と書いてある場合は、「もとにする」数を矢印図の「元の数」だと考えれば良いのです。名前も似ているし、分かりますね?
これで割合の基礎は大丈夫です!
確認テストで定着
□は31の6倍である。□はいくつですか?
( 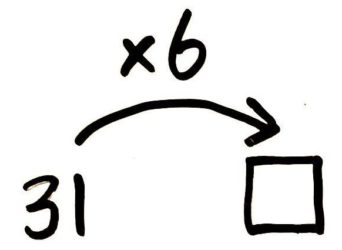 □=31×6=186 )
□=31×6=186 )
143は12の何倍ですか?
→( 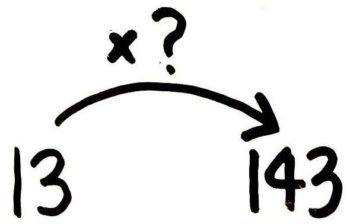 ?=143÷13=11 )
?=143÷13=11 )
12は84の何倍ですか?
→( 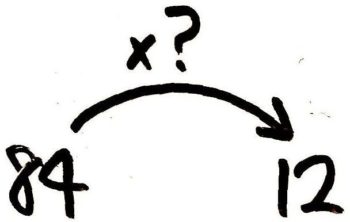 ?=12÷84=1284=17 )
?=12÷84=1284=17 )
19倍して285になる数を求めよ
→( 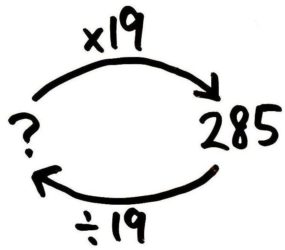 285÷19=15 )
285÷19=15 )
21は□の0.7にあたる。□はいくつか
→( □=21÷0.7=30 )
29をもとにしたとき87の割合はいくつか
→( 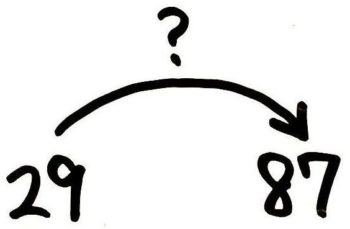 29が元の数になる。?=87÷29=3倍 )
29が元の数になる。?=87÷29=3倍 )
36をもとにしたとき27の割合はいくつか
→( 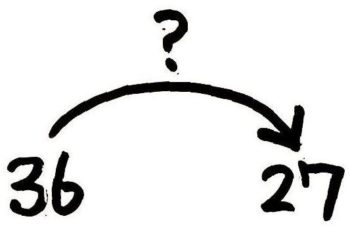 ?=27÷36=0.75倍 )
?=27÷36=0.75倍 )
 爽茶
爽茶復習プリントのダウンロード(2022.4.8)
割合の基礎をサッと復習できる「そうちゃ式 復プリ」です。
右クリックで画像を表示してダウンロードして下さい。
割合の単位(小5)
 爽茶
爽茶ここまで割合を表すのに「○倍」という表現だけを使っていましたが、日常生活では「%(パーセント)」や「割(わり)」を使います。
「100%大丈夫!」とか「バーゲンセールで2割引きで買った♪」などです。
パーセント(百分率)
パーセントは「全体を100等分したうちの何個か」です(だから「百」「分」率)
→あるものを100等分したうちのいくつか
「1%」→あるものを100等分したうちの一つ
「100%」→あるもの全体(×1と同じ)
「%」を「~倍」に直す
パーセントの数字は割合を表すが、そのままでは「矢の数」として計算には使えません。
100で割って小数にするか、100を分母にした分数(約分してもよい)にする必要があります。
●「%」の分母に100をつける
「100%」→「×100100」-(約分)→「×1」
「200%」→「×200100」-(約分)→「×2」
「50%」→「×50100」-(約分)→「×12」
「50%」→「×50100」-(または)→「×0.5」
「25%」→「×25100」-(約分)→「×14」
「25%」→「×25100」-(または)→「×0.25」
「6%」→「×6100」-(約分)→「×350」
「25%」→「×25100」-(または)→「×0.06」
●「%」が小数なら分母に1000や10000を
「12.5%」→「×1251000」-(約分)→「×18」
「25%」→「×25100」-(または)→「×0.125」
パーセントについて詳しく知りたい・問題を解きたい人は関連記事「割合の単位」を見て下さい
歩合(「割」「分」「厘」)
パーセントは外国で生まれた単位ですが、日本で使われてきた単位が「歩合」で「」「」「」の3種類があります。
このままでは計算に使えず、小数や分数の「~倍」に直さないといけません。
まず%に直して、それから~倍に直すのがラクです。
●基本ルール
1割=10%=10100=×0.1
1分=1%=1100=×0.01
1厘=0.1%=101000=×0.01
(例)
4厘3分2割=.420%=20100=×0.2
4厘2割3分=.423%=23100=×0.23
2割3分4厘=23.4%=2341000=×0.234
歩合について詳しく知りたい・問題を解きたい人は関連記事「割合の単位」を見て下さい
「増し」と「引き」
「~%増し」とか「~%引き」と聞いたことはありますね(消費税は10%など)
「増し」=もとの数より大きくなる
もとの大きさ(100%や10割)に加えます。「20%増し」なら「100%+20%」で「120%」つまり「×1.2」になります。
→もとの数(100%、10割)に加える
(例)10%増し
=100%+10%=110%=もとの数×1.1
(例)3割増し
=(10割+3割=13割=もとの数×1.3
または=30%増し=130%=もとの数×1.3
(例)3割2分増し
=32%増し=(100+32)%=132%=×1.32
もとの数より大きくなるので「~倍」に直すと、必ず1より大きい数になります。
「引き」=もとの数より小さくなる
もとの大きさ(100%や10割)から引きます。「20%引き」なら「100%-20%」で「80%」つまり「×0.8」になります。
→もとの数(100%、10割)から引く
(例)10%引き
=100%ー10%=90%=×0.9
(例)3割引き
=10割-3割=7割=×0.7
または=30%引き=70%=×0.7
(例)3割2分引き
=32%引き=100%ー32%=68%=×0.68
もとの大きさより小さくなるので「~倍」に直すと、必ず1より小さい数になります。
「増し」「引き」について詳しく知りたい・問題を解きたい人は関連記事「割合の単位」を見て下さい。
割合の三公式の問題
 爽茶
爽茶ですから「矢印図」が分かっている人はスラスラ出来る?でしょう
「矢印図」から「割合の三公式」へ
矢印図はこうでした♪(忘れた人・知らない人は記事の上の方にある「割合の基礎問題」(矢印図)を読んで下さい)
●矢印図
3つの数が「A×B=C」の関係にある時
矢印の向きに沿ってA,B,Cを並べた図

「2の3倍は6」
「6は2の3倍」

●矢印図による割合の公式
➊さきの数(6)=もとの数(2)×矢の数(3)
❷矢の数(3)=さきの数(6)÷もとの数(2)
❸もとの数(2)=さきの数(6)÷矢の数(3)
そして、学校などで習う「割合の三公式」はこちら
➊割合=くらべる量÷もとにする量
❷くらべる量=もとにする量×割合
➌もとにする量=くらべる量÷割合
よく見ると…似ていませんか?
➊矢の数=さきの数÷もとの数
❷さきの数=もとの数×矢の数
❸もとの数=さきの数÷矢の数
実は、似てるどころか中身は全く同じです。
「矢の数」が「割合」だと説明しましたね?また「もとの数」は「もとにする量」と言葉も似ています。残った「さきの数」が「くらべる量」になります。
ですから…矢印図を書いて計算すれば、途中式も答えも「割合の三公式」で解いたのと同じになります。
つまり、矢印図を使える人は「割合の三公式」を覚える必要は全くありません。
もちろん「くもわ図」を使う必要も全くないでしょう!
三公式の練習
それでは、前の章で学習した「パーセント」「増し引き」も加えた割合の基本問題を解いてみましょう。
「三公式の練習」としています(解説にも三公式を書きます)が、矢印図で解いて構いません。公式を思い出せなくても構いません。正しい式を考え出せればOKです。
いつも最初に「矢印図」を書くか、イメージして下さい。
●例題5-(1)
割合の問題なので、矢印図を書きます。

問題文にある「もとにする」というのは「矢印図」でいう「矢の根元にある数(もとの数)」にするという意味でなので、矢印の根元に20が入ります。問題文で聞かれているのは割合なので「矢の上の数(矢の数)」が「?」になります。

これを見ながら?を出す式を考えます。
「矢の数」を出すので、公式を覚えていればもちろん、覚えていなくても「2×3=6の矢印図」を横に書けば「矢=先÷元」と分かります。
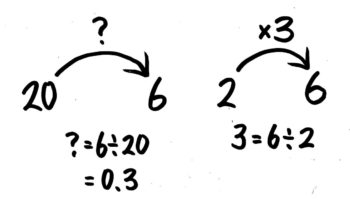
あとは6÷20を計算して0.3が答えと分かります。
0.3
そして0.3をパーセントに直すには100倍すればよいので、0.3×100=30%になります。
30%
ちなみに「割合の三公式」の場合、「割合=くらべる量÷もとにする量」から同じ計算式で同じ答えが出ます。
このように「もとにする」と書いてある場合は、「もとにする」数を矢印図の「元の数」だと考えれば良いのです。名前も似ているし、分かりますね?
●例題5-(2)
「あたる」の意味が分からなくても、とりあえず矢印図を書いてみましょう。
最初に種明かしすると、「~にあたる」というのは「~倍」と同じ意味です。ですから「□は120の0.4にあたる」は「□は120の0.4倍」と同じ意味です。
これをいつもと同じ形に直すと「120の0.4倍は□」「120×0.4=□」になるので、矢印図も書けますね。
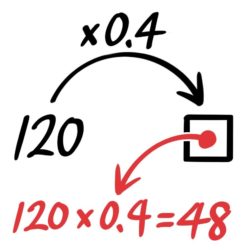
48
ちなみに「割合の三公式」の場合「くらべる量=もとにする量×割合」から同じ計算式で同じ答えが出ます。
このように、「割合の三公式」を使わなくても「矢印図」を書けば計算方法は思いつきますね。というわけでこれ以降も矢印図を使って解いていきます。
ここからは、色んな単位を使う問題です。
●例題5-(2)
「80」%をそのまま使うと大変なことになりますよw
ここまで読んできた人は、90が「元の数」で80%が「矢の数=割合」なのはなんとなく分かるので、このような矢印図は書けるでしょう。
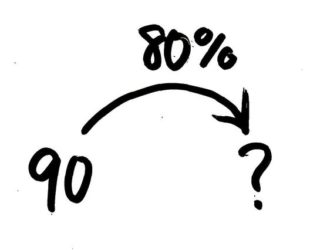
では、?を出す計算式はどうなるでしょうか?80をそのままかけ算にすると…
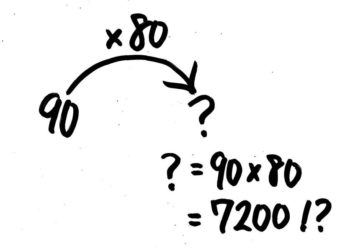
答えがずいぶん大きくなる(それだけで
オカシイわけではありませんが…)
?が7200になります…ここで「80%」の意味を思い出すと「100等分したうちの80個」ですから、元の数よりも小さくなるはず!小さくするには1よりも小さい数をかけないとダメですね(大→小のパターン)

ここで80%を整数・小数に変えたのを思い出しましょう…80%=×80100=×0.8(または×45)でしたね!これを「矢の数=割合」として式を作ればOKです。
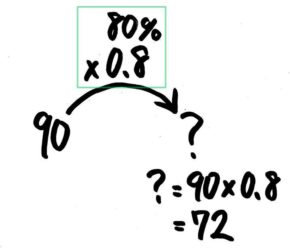
というわけで、90×0.8=72が答えになります。
答: 72
このように、%の数字はそのままではなく「整数・小数・分数」倍に直してから計算に使います。
→数値を100で割って
「×小数」や「×分数」に直してから使う。
(例)
25%→「×0.25」「×25100=×14」
次は歩合です。
●例題5-(3)
パーセントと同じく、歩合もそのままでは計算に使えません。
「□の4割は52」なので、矢印図は書けるでしょう。
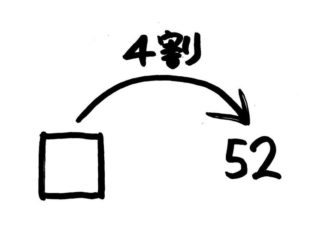
「矢の数=割合」が4割になっていますが、パーセントと同じく整数・小数・分数倍に書き換えましょう。4割=×410=×0.4 を思い出して書き加えます
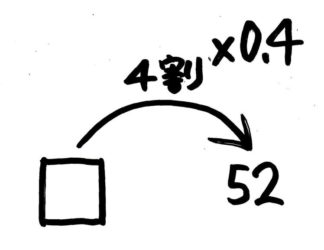
このあとは、逆向きの矢印を書き加えたり、となりに「236の図」を書いたりすれば、□=52÷0.4 という式が作れるでしょう。それを計算して□=130と分かります。
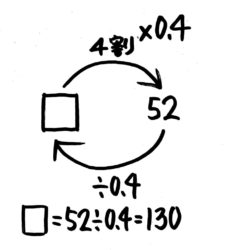
答: 130
このように歩合も「小数・分数」倍に直してから計算に使います。
「×小数」や「×分数」に直してから使う。
一度「%」に直すと分かりやすい
(例)
2割5分=25%→「×0.25」「×25100=×14」
1割2分5厘=12.5%→「×0.125」「×1251000=×18」
次は「増し」「引き」の計算です。
この場合も小数や分数倍に直してから式をたてましょう。「増し」「引き」が不安な人は「増し・引き」の説明を見直して下さい。
●例題5-(4)
「増し」は大きくなる、これが一番大事!
「増し」は大きくなります。「3%増し」はもとの数より3%大きくなって、もとの数の103%、×1.03になります。矢印図にするとこうなるので…
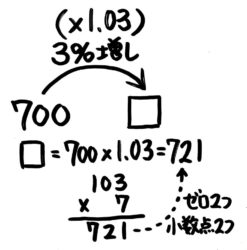
?(先の数)は700×1.03=721になります。
答: 721
小数と大きな数のかけ算のやり方に注意して下さい。小数点や0は取り除いて「7×103」を筆算したあとで戻します。詳しくは「小数の足し算引き算かけ算」内の「小数と大きな数のかけ算」を見て下さい。
実は「先の数(増し・引きの結果)」を出す場合、大人はこういう面倒くさい計算をわざわざしません。こうやります。
まず700円の1%つまり1/100を7円と出しておきます。そして3%は7×3=21円なので、3%増しは700円に21円を足して721円と求めます。
小学生のみなさんも、割合になれてきたら同じ様に計算できるでしょう。
次は「引き」です。
●例題5-(5)
「もとの数」より小さくなります。
「23%引き」なら「もとの数(100%)より23%小さく」なるので100-23=77%、つまり×0.77になります。
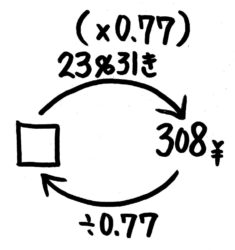
「元の数」を出すので反対向きの矢印を書いて、308÷0.77を行います。ちょっと面倒くさいですが…丁寧に計算して400と分かります。
答: 400円
「元の数」を出す場合は、さっきのようなウラワザはありません。大人にとっても非常に面倒くさいです(汗)
●例題5-(6)
歩合を%に直すと簡単になりましたね♪
2割5分は25%と同じなので、2割5分引き=25%引きで、元の数の100-25=75%、×0.75と分かります。
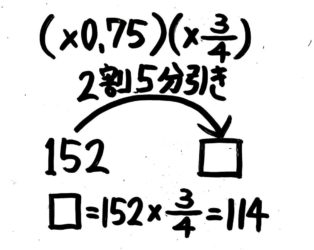
0.75=3/4と思い出せれば、計算は簡単になります。
答: 114
●例題5-(7)
歩合を%から小数にして図を書きましょう。
3割6分=36%なので、3割6分増し=136%、×1.36と分かります。図を書くと「元の数」を出すと分かるので、反対向きの矢印を書いて(またはイメージして)
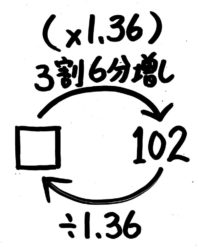
102÷1.36を計算して、75と求めます。これも面倒くさい計算でした。
答: 75
確認問題をどうぞ
2019.12.作成中
復習プリントのダウンロード(2022.4.8)
割合の基礎をサッと復習できる「そうちゃ式 復プリ」です。
右クリックで画像を表示してダウンロードして下さい。
オススメの学習教材
 爽茶
爽茶●毎日のドリルシリーズ(管理人による紹介)は学年別分野別の薄い問題集で気軽に取り組めます。「小学5年の数・量・図形(毎日のドリル)」
●「いっきに極める算数(割合と比例)」
●「絵本仕立て 割合がわかる本」
●「算数少女ミカ 割合なんて、こわくない!」
「分かりやすい」と評判の
「そうちゃ式のおすすめ利用法」が参考になるかも
今なら14日間無料♪この期間内に利用を停止すれば料金は一切かかりません。この機会に試してみては?
オリジナル教材のご案内
御三家・早慶付属など難関・人気の中学に合格した2025年度の受験生達から大好評!
分かりやすいのはもちろん、スキマ時間にお子様一人で反復定着できますよ
人気教材はこちら(クリックするとショップ内教材ページにジャンプ)
●歴史 ●時事問題(2025年) ●世界地図 ●世界遺産
■仕事ニュートン算 ■食塩水 ■売買損益
★月の形 ★電流 ★水溶液/気体の性質
その他にも社会/理科/算数の教材がございます。興味がある方は公式ストアへどうぞ


