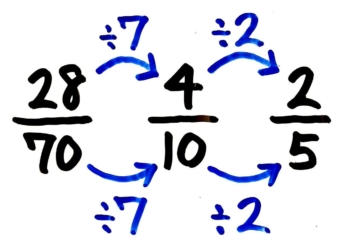「約分の仕方・ルールを忘れた」「既約(きやく)分数って何？」という小学5年生の方、大丈夫ですよ！東大卒講師歴20年の図解講師「そうちゃ」が「約分」の方法や「既約分数」について分かりやすくまとめました♪
サッと復習したい人は目次の「まとめと確認テスト」をクリックして下さい。
目次(クリックでジャンプ)
分数操作(約分と倍分)の基本ルール
爽茶こんにちは！「そうちゃ」@zky_tutor(プロフィール)です。
ルールを理解する！
例題1(分数操作のルール)
例題1(1)
12はいつもの円形のパンを二等分したうちの1ピースです。
スパッと「半分」ですね
つぎに□4を書きます。分母が4なので、四等分することはわかります。
さっきの12と並べると…
四等分したうちの2ピースなら、12と同じく「半分」になるので、□=２と分かりますね！
つまり、12=24ということですね。2
例題1(2)
12は「半分」と言う意味でした。この小問では一個のパンを六等分しています。
六等分したうちの「半分」は３ピースなので36になり、□は3と分かります
3
例題1-(3)
小問(1)(2)から、
と分かります。
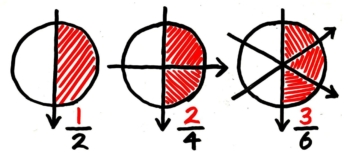
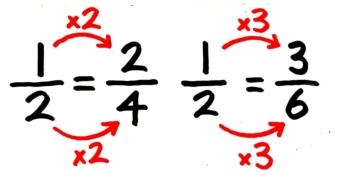
3つの分数は書いてある数字は違いますが、同じく「半分」を表しており数としての大きさは同じです。
そして3つの分数をよく見ると、12
=24では、分子が1→2と2倍になると分母も2→4と2倍になり、12
=36では分子が1→3と3倍になると分母も2→6と3倍になっています。
つまり、分子と分母に同じ数をかける限り大きさは変わっていません。
同じ数をかけても
同じ数をかけても数としての大きさは「半分」で変わらないということは
12は100200でもあり100000200000でもあるということです。
面白いですね！
(^O^)
また、2→1と4→2、3→1と6→3と逆向きに見れば、分子と分母を同じ数で割る限り大きさは変わっていません。
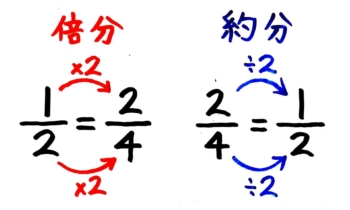
このように、分数の分母と分子に同じ数をかけたり、同じ数で割ったりしても、数としての大きさは変わらないのですね。これが分数の操作の基本ルールです
分母と分子に同じ数をかけても(倍分)
同じ数で割っても(約分)
大きさは変わらない
(分母・分子を同じ数で)割る方を「約分(やくぶん)」かける方は「倍分(ばいぶん)」と言います。
倍分と約分のうち、使うことが多いのは約分です。試しに、約分の練習をしてみましょう
約分を練習する♪
例題2(分数の約分)
まず、小さい数で割るのが基本です
約分するときは、まず、2,3,5のような小さい素数で分母・分子を両方共割れないか、つまり、分母と分子が両方共2,3,5の倍数になっているかを考えます。これが良くわからない人は過去の記事「約数・素数・素因数分解」や「倍数の見分け方」を復習して下さい。
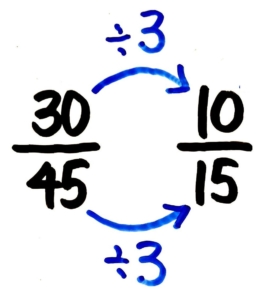
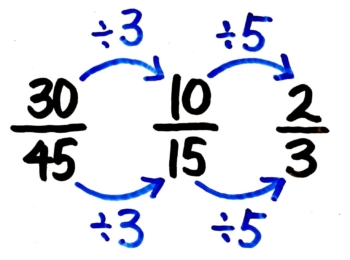
さて、この問題の分母30と分子45は両方共2の倍数か考えます…ちがいますね(分母45は1の位が偶数になっていないので)。
次に両方とも３の倍数か考えます…そうですね！(両方とも各位の和が3の倍数) そこで、両方を3で割ります(約分)
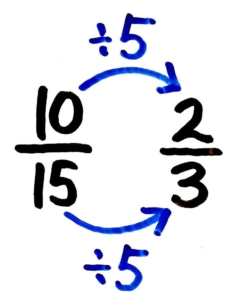
次に、今の約分の結果1015を更に約分できないか考えます。10と15は両方とも５の倍数(1の位が0か5)なので両方を５で割る(約分する)と
今度は23を約分できないか考えます…2と3を両方割れる数は１しかないので、これで約分は終了！です。
答: 23
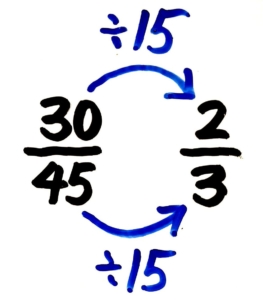
もしかしたら「両方とも15で割れる!」と気づいて、こんなふうに一気に答えを出したかもしれませんね。
これでも正解です！ただ、パッと思いつかない場合は悩んでないで小さい数でコツコツと割っていきましょう
さて、例題で見たように、約分は限界があります。そして今の23 のように「これ以上約分できない分数」を「既約(きやく)分数」と呼びます。
一方、倍分の方は
12→1020→100200→1000020000… というように無限にできます。
「約分」＝分母・分子を同じ数で割ること
「既約分数」→これ以上約分出来ない分数
では、約分の問題を解いてみましょう
類題2(約分)
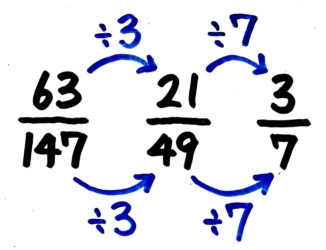
(1)2870 (2)126294
類題2-(1)
分子・分母の両方とも割れる数がないかを考えます。この問題では、分子が28と分母が70なので…
その数で約分すると…
さらに約分すると…
さらに約分すると…
さらに25を約分しようとしても、2と5はともに1以外では割れない(既約分数)ので、ここで終了となります。
答: 25
類題2-(2)
分子や分母が大きな数の場合も、まずは2,3,5,のような小さな素数で割っていきましょう。
この問題のように分子や分母が大きな数の場合も、まず 2,3,5の倍数になっていないかを考えます。(「倍数の見分け方」を参照)
分子が126、分母が294 はともに一の位が偶数なので、2の倍数と気付きます。
126294 →(分母分子を2で割る)→63147
次に、分子63と分母147は、ともに各位の和が3の倍数なので、63と147自体も3の倍数と気付きます。
63147→(分母分子を3で割る)→2149
さらに、分子21と分母49は両方とも7の倍数なので
2149 →(分母分子を7で割る)→37
これ以上は約分できない(既約分数)ので、ここで終了となります。
答: 37
これで倍分と約分の練習は終了です。次は、倍分と約分を使った問題です。
約分と倍分を使った問題
爽茶解き方を理解する♪
例題3(約分倍分の利用)
23=□6=12□
まず左の2つの分数だけに注目！
まず左側の23=□6 に注目すると、分母が3→6に2倍されているのに気づきますね。同じように分子も同じように2倍して2→4で□は4になります。
23-(分子2倍)→-(分母2倍)→46
次に右側の□(4)6=12□に注目すると、分子が4→12と3倍されているのに気づきますね。同じように分母も3倍して6→18で□は18になります。
23-(分子2倍)→-(分母2倍)→46-(分子3倍)→-(分母3倍)→1218
したがって、答えは ３と18 です。
答: 3,18
こんな感じで、まずは2つの分数に注目して、分母と分子のどちらかが「×いくつか」または「÷いくつか」になっているか発見していきます。では、練習してみましょう！
練習問題で定着
類題3(約分倍分)
(1)14=□40=5□
(2)735=1□=□10
(3)1=□7=8□
(4)1830=15□
(5)924=□56
類題3-(1)
類題3-(2)
今度は●分ですね。
類題3-(3)
小４の時に 1=AAを習いましたね。
次は少し難しいかもしれません。
類題3-(4)
一度◯分してから●分します
類題3-(5)
小問(4)と同じように。
これで分数操作の問題は終了です。
以上で今回の問題は終了です。お疲れ様でした！
これで必要に応じて分数をいろんな形に変身！させることが出来ますね
まとめと確認テスト
このページの内容をまとめました。空欄をクリックすると答えが表示されます。
分数操作のルール=分母と分子には同じ操作をする
◆かけ算をしても大きさは変わらない(倍分)
(例1)57=(20)28 (例2)49=20(45)
◆割り算をしても大きさは変わらない(約分)
(例1)624=(3)12 (例2)2540=5(8)
これ以上約分出来ない分数=「既約分数」
(例){927,326,1025}のうち既約分数はどれか
→( 326 )
次のステップへ♪
爽茶今回は分数を操作して、色いろな形に変形しました。だいぶ分数に慣れてきたのではないでしょうか？
「分数の総合案内」から「通分」に進んで下さい