「小数の計算がよく分からない…苦手！」という小学生のあなた、あなたが心配している以上に小数は重要です。
小数が分からないと「単位」「割合」など他の重要分野も分からなくなってしまいます！
じゃあどうすればいいの…と思ったかもしれませんが、安心して下さい！東大卒講師歴20年の図解講師「そうちゃ」が小数の基本から分かりやすく教えます。
この記事を読んで練習すれば小数のルールがスッキリ頭に入ります。読み終わる頃には小数が得意になっているかも♪
下の目次で、例えば「小数の割り算」など好きな項目をクリックすればジャンプできますよ。
目次(クリックでジャンプ)
小数の基礎(小3)
爽茶こんにちは！「そうちゃ」@zky_tutor(プロフィール)です。
小数の基礎から見ていきます。小数とは？
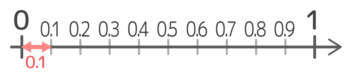
「小数」とは1より小さい数です。「.」(小数点)より右に行くほど小さい数になります。
0 . 1 2 3
「1」→小数第1位
「2」→小数第2位
「3」→小数第3位
そして、小数の大きさは「1」を基準に決められています。
●「0.1」=0から1を十等分した大きさ
●「0.01」=～を百等分した大きさ
●「0.001」=～を千等分した大きさ
反対から言うと、0.1が10個集まると1になり、0.01が100個集まる、0.001が1000個集まると1になります。
小数のつくり
例えば「1.234」という小数を分解すると、1+0.2+0.03+0.004になるので、「1.234」は1が1個、0.1が2個、0.01が3個、0.001が4個集まって作られていると分かります。
+0.234
+0.034
+0.004
+1.234
確認テストをどうぞ。
1が2個、0.1が3個、0.01が4個、0.001が5個集まった数は？
→( 2+0.3+0.04+0.005=2.345 )
1が3個、0.01が3個、0.001が3個が集まった数は？
→( 3+0.03+0.003=3.033 )
0.1が18個、0.001が13個が集まった数は？
→( 1.8+0.013=1.813 )
小数のつくり(分数から)
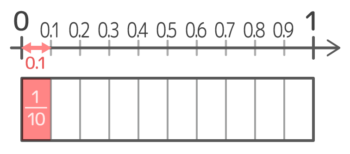
0.1は1を十等分したものなので、110と等しくなる。
同様に、0.01は1100、0.001は11000と等しくなる。
0.1=110
例えば「110が1個、1100が2個、11000が3個集まって作られた数」は、0.1が1個、0.01が2個、0.001が3個集まった数と等しいので、0.123になる。
試しにテストしてみましょう。
1が3個、110が2個、1100が1個集まった数は？
→( 3+0.2+0.001=3.21 )
110が12個集まった数は？
→( 0.1が12個なので、1.2 )
110が24個、1100が6個、11000が13個集まった数は？
→( 2.4+0.06+0.013=2.473 )
爽茶小数点の移動(小4)
やり方と意味
左右どちらに動かすかで意味が変わります。
◆数を10倍100倍する→小数点を右にずらす
(例)1.5を100倍する
◆数を10や100で割る→小数点を左にずらす
(例)1.5を100で割る
右に動かす=数を大きくする
数を10倍・100倍する時(大きくする時)は小数点を右に1ケタ・2ケタずらします。
右に1ケタずらす
右に2ケタずらす
左に動かす=数を小さくする
反対に、数を10で割る、100で割る(110,1100する)時(小さくする時)は小数点を左に1ケタ・2ケタずらします。
左に1ケタずらす
左に2ケタずらす
確認テストをどうぞ
「12.3」を10倍すると？
→( 小数点を右に1ケタ動かす )→( 123→ 123 )
「12.3」を100で割ると？
→( 小数点を左に2ケタ動かす )→( 0123→ 0.123 )
「12.3」を1000倍すると？
→( 小数点を右に3ケタ動かす )→( 12300→ 12300 )
小数点と単位(小4～)
「小数点の移動」を使うと、単位を別の単位に変えるのが簡単になります。
例えば、1km=1000m なので、kmをｍに直す時は1000倍つまり小数点を3つ右にずらすだけでOKです。
逆にmをkｍに直す時は1000で割るつまり小数点を3つ左にずらせばOKです。
爽茶小数計算のまとめ
小数の計算はそれぞれ筆算のやり方(小数点の扱い方)が異なります。
◆足し算・引き算
→小数点を揃えて筆算を行う
◆かけ算
→小数点を取って筆算した後で小数点を戻す
◆割り算
→割る数と割られる数の小数点を同じだけずらして筆算
◇商はずらした小数点を使うが、
◇余りはもとの小数点を使う。
それぞれについてもう少し詳しくまとめます。
小数の足し算・引き算(小3～小4)
小数の足し算・引き算は小数点をそろえて行います。
→小数点をそろえて筆算
(例)15.1+1.51
Good
そろっている
+11.51
16.61
Not Good
そろってない
+1.51
2??2
確認テスト(作成中)
爽茶小数のかけ算(小4・小5)
小数をかける意味
1より小さい数をかけると答えはもとの数より小さくなります。
●1をかけると、答えは元の数と同じ
(例)5×1=5
●1より小さい数をかける
答えは元の数より小さい
(例)5×0.8=4
●1より大きい数をかける
答えは元の数より大きい
(例)5×2＝10、5×1.2=6
小数同士のかけ算
足し算引き算と違って小数点を使わず筆算します。そして筆算の答えに小数点を戻します。
→小数点を取って筆算して、小数点を戻す
(例)0.27×0.038
- 問題の数の小数点を右に動かして整数にする
027000380
(合計で5ケタ
右に動かしている) - 整数のかけ算の筆算をする
27
x 38
216
0810
1026 - 右に動かしたケタ数だけ小数点を左に戻す
001026→
001026(5ケタ左に動かすと答え)
小数と0のある数のかけ算
小数点も0もとって筆算を行い、小数点以下の数と0の数を差し引きして小数点を動かします。
→0と小数点をとって筆算。
答えに０と小数点を「戻す」
(例) 27000×0.38
→27✕38=1026→10260
( 0は3つ小数点以下は2つなので
差し引き0を一つ付ける )
→1026000→10260
確認テスト(作成中)
覚えておくべき小数のかけ算
以下のかけ算を覚えると計算が楽になります。
かけて１になるかけ算を覚える
①0.5×2=1
➁0.25×4=1
③0.125×8=1
確認テストをどうぞ
0.25×12=( 0.25×4×3=1×3=3 )
0.125×160=( 0.125×8×20=1×20=20 )
爽茶小数と概数(小4)
小数の割り算に必要なので「小数と概数」を簡単に説明します。
概数の決め方には三種類ありました。
❶「小数第□位を四捨五入」→指定された位を四捨五入
(例)1.234を小数第二位を四捨五入→「3」を四捨五入(切り捨て=ゼロにする)して1,200→1.2になる
❷「□の位までの概数」→□の一つ下の位を四捨五入
(例)1.234を四捨五入して小数第二位までの概数→小数第三位を四捨五入→「4」を四捨五入(切り捨て=ゼロに)して1.230→1.23になる
❸「上から□ケタの概数」→□より一つ多い位を四捨五入
(例)1.234を四捨五入して上から2ケタの概数→上から3ケタ目を四捨五入→「3」を四捨五入(切り捨て=ゼロに)して1.200→1.2になる
切り捨て切り上げ四捨五入のやり方は整数と変わりませんが、答え方に注意が必要なこともあります。
テストしてみましょう
小数第二位を四捨五入して「42.537」を概数にすると？
→( 小数第二位は3なので切り捨てて42.5 )
「42.537」を小数第二位までの概数にすると？
→( 小数第三位の7を四捨五入して42.54 )
「42.537」を上から3ケタの概数にすると？
→( 上から4ケタ目の3を四捨五入して42.5 )
爽茶小数のわり算(小4・小5)
小数÷整数(小4二学期)
割られる数の小数点を上にも移します。
→割られる数の小数点を上にも移すだけ(左)で、
解き方自体は整数÷整数(右)と同じ♪
9)117
97
127
27
20
9)117
97
127
27
20
余りがある場合は、余りにも小数点をおろします。
小数点を上に移すだけでなく、
余りまで下ろしてくる
3)824
624
224
214
214
確認テスト(作成中)
詳しい説明を見たい、問題を解きたいという人は「小数の割り算」内の「小数÷整数」を見て下さい。
小数÷小数(小5一学期)
小数で割る場合は、小数点を動かして筆算の準備をします。
- 割る小数が整数になるように小数点を右に動かす。
7
31)837 - 割られる小数の小数点も同じケタ数だけ右に動かし、上にも移す
7
31)837
割り算を行ったら、余りの小数点を決めます。
答えの小数点はずらした小数点を使い、あまりの小数点はもとの小数点を使います。
◆答え→動かした小数点を使う
◇余り→もとの小数点を使う！
- 筆算の準備
割る数と割られる数の小数点を右に動かし上にも移す1
35)750 - 割り算
指定された位まで割り算をする21
35)750
700
450
35
15 - 余りを確定
もとの小数点を下ろして余りを確定する。21
35)750
700
450
35
015
確認テスト(作成中)
爽茶小数と分数(小3～小5)
「分数が嫌い！小数の方が好き」という人が多いですが、小数よりも分数の方が便利(中学以降はほとんど分数)
0.1=110
小数は必ず分数に直すことができるので、直せるようにしておきましょう。
●小数第一位までの数→10を分母につけて約分
(例)0.4→410→25
●小数第二位までの数→100を分母につけて約分
(例)0.15→15100→320
●小数第三位までの数→1000を分母につけて約分
(例)0.125→1251000→18
確認テスト(作成中)
爽茶小数の応用問題(中学受験)
中学受験用の小数の応用問題は、姉妹サイト「そうちゃ式受験算数(新1号館)」の「小数の応用問題」を見て下さい。
爽茶以上で小数のまとめ記事は終了です。
歴史を学習する小学生の保護者の方へ
年表,年号,地図,書き取りテストなど400枚のプリントがセットになったそうちゃ式オリジナル教材が8/25(日)までお買い得価格！興味がある方はコチラへ
2023年度生徒さん募集
2023年度の生徒さんの募集を開始しました(対面授業の一次募集)
東武野田線・伊勢崎線沿線にお住まいの新5年生で予習シリーズをベースにされている方が対象です。
詳しくはコチラのページを御覧下さい
新4年生の方を対象に学習相談/授業を実施します(2次募集はサピックス新越谷校・南浦和校の方のみ対象。締め切り1/27)。応募はコチラから
中学受験でお悩みの方へ
爽茶「中学受験と高校受験とどちらがいいの？」「塾の選び方は？」「4年次・5年次はどう勉強すればよい？」「志望校の過去問が出来ない…」など
様々なお悩みへのアドバイスをまとめたので参考にして下さい。
もしかしたら、自分だけで悩んでいると煮詰まってしまい、事態が改善できないかもしれません。講師経験20年の「そうちゃ」に相談してみませんか？対面/オンラインの学習相談を受け付けているので、ご利用下さい。
Html図保存セクションここから
0 . 1 2 3
「1」→小数第1位
「2」→小数第2位
「3」→小数第3位
●「0.1」=0から1を十等分した大きさ
●「0.01」=～を百等分した大きさ
●「0.001」=～を千等分した大きさ
Html図保存セクションここまで