小学5年生】倍数・約数と公倍数・公約数とは？分かりやすく総まとめ！

(1)7の倍数とはどういう数か？2通りで表わせ
→➀( 7を1倍・2倍…した数
)
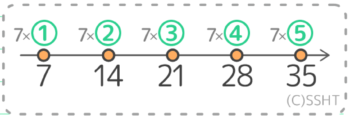→➁( 7で割り切れる数 )

(2)23の倍数を小さい方から3つ書け
→( 一番小さいのは23×1=23、二番目が23×2=46、三番目が23×3=69 )

(3)偶数か奇数か判定しなさい

次の数が〔〕内の数の倍数になっているか「O」「X」で答えなさい
①943〔2〕→( 1の位が3なのでX )
②291〔3〕→( 2+9+1=12が3の倍数なのでO )
③217〔4〕→( 下2ケタ17が4の倍数でないのでX )
④395〔5〕→( 1の位が7なので○ )
⑤846〔6〕→( 1の位が6で、8+4+6=18が3の倍数なので○ )

(1)3と5の最小公倍数を求めなさい
→( 5の2倍10は3の倍数では無い。5の3倍15は3の倍数でもあるので、最小公倍数は15 )

(2)3と4の公倍数はどのような数か？一言で表現しなさい
→( 3と4の最小公倍数が12なので、3と4の公倍数は12の倍数 )

(4)6でも8でも割り切れる数はどのような数か？
→( 6でも8でも割り切れる数=6と8の公倍数=6と8の最小公倍数の倍数。6と8の最小公倍数は24だから、6でも8でも割り切れる数は24の倍数 )
(3)6と9の3番目の公倍数は？
→( 6と9の最小公倍数が18なので、6と9の公倍数は18の倍数。その3番目は18×3=54 )

タテ3cmヨコ4cmの長方形をすき間無く並べて正方形を作る。

(1)一番小さい正方形の一辺は何cmか？
→( 3と4の最小公倍数 )を求めれば良い
→( 4を2倍→8は3の倍数になっていない。4を3倍→12は3の倍数になっているので最小公倍数。一番小さい正方形の一辺は12cm )

(2)その時、長方形を何個使っているか？
→たて方向には( 12÷3=4 )個、よこ方向には(  12÷4=3 )個使っている
→合計では( 4×3=12 )個。

バスAは10分おきに、バスBは14分おきにバスステーションから出発します。ABとも最初のバスは午前7時に同時に発車します。

(1)ABが次に同時に出発するのは何時何分ですか？
→( ABが同時に出発するのは10と14の最小公倍数は70なので70分ごと )
→( 次に同時に出発するのは7時の70分後で7時70分=8時10分 )

(2)最初の1回を入れてABが3回目に同時に出発するのは何時何分ですか?
→( 8時10分の70分後だから8時80分=9時20分 )

20の約数を全て書き出しなさい
→( 20=1×20=2×10=4×5なので 1,2,4,5,10,20 )

(1)12と18の公約数を求めなさい
→( 12の約数は1,2,3,4,6,12で18の約数は1,2,3,6,9,18なので、共通する約数は1,2,3,6 )
(2)12と18の公約数はどのような数か？一言で表現しなさい
→( 12と18の最大公約数が6なので、12と18の公約数は6の約数 )

タテ30cmヨコ42cmの長方形の紙がある。この紙をできるだけ大きい正方形に切り分ける。正方形の一辺は何cmになるか？
→( まず30と42の最大公約数を求める )
→( 30の約数は1,30,2,15,3,10,5,6で、この中で42の約数にもなっている一番大きな数は6なので、正方形の一辺は6cm )

全部でいくつの正方形に切り分けられるか？
→( タテ方向には30÷6=5枚、横方向には42÷6=7枚、合計で5×7=35枚 )

何人かの生徒がアメを同じ個数ずつとガムを同じ個数ずつ持って集まったところ、アメは合計35個でガムは合計21 個になった。生徒の人数は一番多くて何人か？
→( 35と21の最大公約数を求めれば良い。 )
→( 21の約数は1,21,3,7で、この中で35の約数にもなっている一番大きな数は7。生徒の人数は7人 )

生徒達はアメとガムを何個ずつ持ってきたか？
→( アメは35÷7=5個ずつでガムは21÷7=3個ずつ )