「約数・公約数って何？」「約数・公約数を全部書けって言われたんだけど…」とお困りの小学5年生の方、ご安心下さい！
東大卒講師歴20年の図解講師「そうちゃ」が分かりやすく説明します。
記事を読んで問題を解けば、約数・公約数の基本知識は全部分かっていることでしょう。
目次(クリックでジャンプ)
「約数」の意味
こんにちは！「そうちゃ」@zky_tutor(プロフィール)です。
「やくすう」って何でしょうね？
1-1:約数の意味
「ある数AをBで□できる時、BをAの約数と言う」
ヒント
まず倍数の意味を思い出しましょう。
解説
倍数の意味を思い出してください。例えば、6の倍数はどんな数でしたか？
約数はその逆になります。
「6の約数」=「6を割り切れる数」ということです。
したがって、「ある数AをBで割り切れる時、BをAの約数という。」が答えになりますね
問題を解く基本ですので覚えて下さい！
約数＝他の数を割り切れる数
これを使って、次の例題です
2:約数と倍数の意味
「A=B×Cの時、□は◯と●の倍数で◯と●は□の約数」
ヒント
誘導に乗って考えましょう
解説
分かりやすいように「A＝B×C」のA,B,Cを適当な数字にしましょう。
今日は「6＝2×3」にします。
「6＝2×3」の場合、6は2の倍数で、3の倍数でもあります。
また、２と３は両方とも６を割り切れる数＝「６の約数」です。
ここで「6＝2×3 」を「A＝B×C」 に戻すと答がわかりますね
AはBとCの倍数。また、BもCもAの約数です。
AはBとCの倍数で
BとCはAの約数
ｺﾞﾁｬｺﾞﾁｬしてきましたね…
(^_^;)
ここでは「かけ算にすれば約数が分かるんだ」と考えておけばOKです！
約数の求め方としてまとめると、こうなります
●A＝B×C の時、BとCはAの約数である。
(例)6=2×3なので、2と3は6の倍数
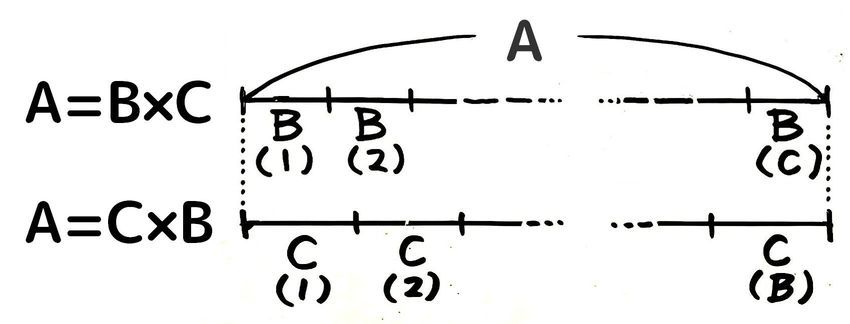
後の回に出てくる問題で使うので、これを線分図にしてみます。線分図基本講座で出てきた「かけ算の線分図」の形を使います
((リンク))
「A=B×C」は「BをC個つなげるとAになる」という意味ですので、線分図はこうなります。
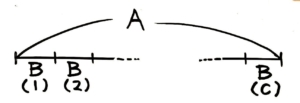
Bが(C)個並んでいる
また、「A=B×C」は「A=C×B」とも言えるので、こういう線分図も描けます。
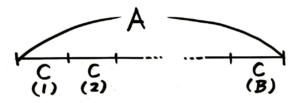
CがB個並んでいる
書けるように練習しておきましょう！
約数の意味と求め方がわかったと思うので、問題を解いてみましょう
約数を求める問題
(書き出し式)
求め方を理解
まず、導入形式でやり方を覚えましょう！
3:約数の書き出し
○を1から順に2,3…と増やしていき、できるだけ多くの「組み合わせ」を書きなさい。
ヒント
「組み合わせ」であることに注意!
解説
ある数を「○×●」というかけ算の形に直すことを「分解」と呼びます。
なじみがあるのは、九九に出てくる組み合わせでしょうか
例えば、(A)２×９＝18 とか(B)３×６＝18ですね。
この問題では「○を1から順に2,3…と増やしていき」という指定があるので、それに沿って書いていきましょう
初めは○＝１なので、18=1×● に直します。●はいくつでしょうか？
●＝18 なので、「1と18」という組み合わせが出来ました。
次は○＝２です。18＝2×●に直すと●はいくつですか？
●＝９なので、「2と9」という組み合わせが出来ました。
あとは、◯＝3,4,5,6…と増やしていくと、どんな組み合わせができるか書いていきます。
○＝３の時、18＝３×６→「３×６」という組み合わせ
○＝４の時、18＝４×… 直せません
○＝５の時、18＝５×… これも直せず
○＝６の時、18＝６×３→「６×３」ができそうですが！
さっき「３×６」という組み合わせが出来ていました。「３×６」と「６×３」は同じ組み合わせです。
このように同じ組み合わせが出てきたら、そこで終了！です
今の作業を表にまとめるとこうなります。
18=◯×□への分解
| ◯ | 1 | 2 | 3 | 4 | 5 | 6 | 7～ |
| 分解 した形 |
1×18 | 2×9 | 3×6 | できない | できない | と同じ) |
(終了) |
1×18,2×9,3×6という３つの組み合わせが答えです。
このように分解できると約数が分かりますね
ヒント
「A=B×C」ならBとCがAの約数なので小問1の答えを見れば18の約数は分かりますね。
解説
小問1から、18は「18＝1×18」「18＝2×9」「18＝3×6」という3つの形にできると分かるので、18の約数は…
1と18、２と９、３と６ と分かります。これらを小さい順に並べて答えになります。
次は、これを利用する問題です。
ヒント
悩まずに足しましょう。
解説
小問2の答えをすべて足すと
1+2+3+6+9+18=39 になりますね
書き出しによる約数の求め方が分かりましたか？今度は導入なしで答えを出してみましょう！
( ･`ω･´)
類題で定着
3:約数の書き出しと合計(1)
解説
まず12の約数を求めます。
12を小さい数字で始まるかけ算に分解して、組み合わせを書き出していきます。
1×12→「1と12」
2×6→「2と6」
3×4→「3と4」
4×3→「4と3」は「3×4」と同じ組み合わせなのでここで終了です
以上より、12の約数は1,12,2,6,3,4の6つと分かります。
次に、約数の合計を求めます。
先程出した約数を合計して、1+12+2+6+3+4=28となります。
できましたか？もう一問練習しましょう。
3:約数の書き出しと合計(2)
解説
30を分解していきます。
1×30
2×15
3×10
4×…できません
5×6
6×5 これは「5×6」と同じなので、ここで終了。
以上より、30の約数は 1,2,3,5,6,10,15,30 の8つと分かります。
これらを合計すると、1+2+3+5+6+10+15+30=72です
最後はちょっと面倒くさい問題です。
3:約数の書き出しと合計(3)
アドバイス
途中でメゲずにやりきって下さい…
解説
まず210を分解して約数を求めましょう！
1×210
2×105
3×70
4×…できません
5×42
6×35
7×30
8×…できません
9×…できません
10×21
11×…できません
12×…できません
13×…できません
14×15
15×14 これは「14×15」と同じなので、ここで終了です
以上より、210の約数は1,2,3,5,6,7,10,14,15,21,30,35,42,70,105,210 の16個です。
いま出した約数を合計すると、
1+2+3+5+6+7+14+15+21+30+35+42+70+105+210＝546 です。
お疲れさまでした！
約数の基本問題は以上です。
約数のまとめ
●約数の意味(例:Aが6の約数)
❶Aは6を割り切れる
❷「6＝A×◯」に分解できる。
●約数の求め方(書き出し式)
(例:6の約数を求める)
6＝1×6＝2×3と分解して1,2,3,6
約数の問題プリントダウンロート
(準備中)
約数の次は「公約数」を学びます
公約数の意味
公約数の「公」は2つ以上のモノに共通するという意味です。
だから「公」約数は「2つ以上の数に共通する約数」という意味になりますね♪
例題で確認しましょう！
求め方を理解
4:公約数の意味
ヒント
約数を書き出すときは、かけ算に直していきましたね
解説
まず、８の約数を書き出すと
8をかけ算に直すと、8＝1×8、8＝2×4 にできるので、8の約数は1,2,4,8 ですね
次に、12の約数を書き出すと
12＝1×12、12＝2×6、12＝3×4 なので、12の約数は 1,2,3,4,6,12 ですね
では、共通するもの(つまり公約数)は何ですか？
共通するものは…1,2,4の3つですね。
12の約数：1,2,3,4,6, 12
ところで、「公倍数は最小公倍数の倍数」でした。公約数にも同じような性質があります。
今の答え(公約数)の1,2,4は一番大きな公約数(最大公約数)である「4」の約数になっています。
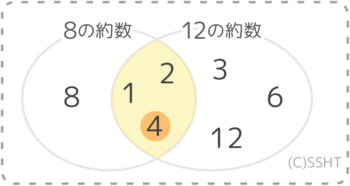
つまり、公約数は最大公約数の約数になります。
→2つ以上の数に共通する約数
＝最大公約数の約数
(例)8と12の公約数
→8と12の最大公約数は4なので
→8と12の公約数は4の約数
前回の公倍数では「最小」公倍数がポイントでした。今回の公約数と最小・最大…ゴチャゴチャするので一度まとめます。
(^_^;)
| 公約数 | 公倍数 | |
| 意味 (別表現) |
2つ以上の数に共通する約数 (AとBを割り切れる数) |
2つ以上の数に共通する倍数 (AとBで割り切れる数) |
| キーとなる数 | 最大公約数 (一番大きい公約数) |
最小公倍数 (一番小さい公倍数) |
| 単純化すると | 最大公約数の約数 | 最小公倍数の倍数 |
「倍数に最大は無いので『最小』は倍数の方」と覚えるのが簡単でしょうか？
( ・Θ・)
類題で定着♪
4:公約数を求める(1)
解説
18の約数は 1,2,3,6,9,18 で27の約数は 1,3,9,27 なので、公約数(共通するもの)は…1,3,9ですね。
27の約数：1,2,3,6,9,18,27
そして、この３つは最大公約数９の約数になっていますね。
最後の問題です。
4:公約数を求める(2)
解説
16の約数は1,2,4,8,16
24の約数は1,2,3,4,6,8,12,24
40の約数は1,2,4,5,8,10,20,40
なので、公約数は1,2,4,8 ですね。
16の約数:1,2,4,4,8,8,8,16,16,16
24の約数:1,2,3,4,6,6,8,12,12,24,24,24
40の約数:1,2,4,4,5,8,8,10,20,20,20,40,40
そして先程見たとおり、この4つの数は最大公約数8の約数になっています。
以上で、公約数の基本も終了です！
公約数の問題
プリントダウンロード
(準備中)
無断転載引用はご遠慮ください。
→公約数公倍数の総合案内から他の記事も読んで下さい！
おすすめ教材
爽茶オススメ問題集
●「毎日のドリル」(学研)はスマホアプリとの連携でやる気をアップできる問題集です。(くわしい案内はこちら)。
●約数/公約数だけを応用問題まで特訓したい人には「約数・公約数」(サイパー算数)がオススメ
「分かりやすい！」と評判の
今なら14日間無料♪この期間内に利用を停止すれば料金は一切かかりません。この機会に試してみては？
歴史を学習する小学生の保護者の方へ
年表,年号,地図,書き取りテストなど400枚のプリントがセットになったそうちゃ式オリジナル教材が8/25(日)までお買い得価格！興味がある方はコチラへ
2023年度生徒さん募集
2023年度の生徒さんの募集を開始しました(対面授業の一次募集)
東武野田線・伊勢崎線沿線にお住まいの新5年生で予習シリーズをベースにされている方が対象です。
詳しくはコチラのページを御覧下さい
新4年生の方を対象に学習相談/授業を実施します(2次募集はサピックス新越谷校・南浦和校の方のみ対象。締め切り1/27)。応募はコチラから
中学受験でお悩みの方へ
爽茶「中学受験と高校受験とどちらがいいの？」「塾の選び方は？」「4年次・5年次はどう勉強すればよい？」「志望校の過去問が出来ない…」など
様々なお悩みへのアドバイスをまとめたので参考にして下さい。
もしかしたら、自分だけで悩んでいると煮詰まってしまい、事態が改善できないかもしれません。講師経験20年の「そうちゃ」に相談してみませんか？対面/オンラインの学習相談を受け付けているので、ご利用下さい。