「分数が苦手だから何とかしたい!」「苦手にならないように予習したい」という小学5年生と保護者の方、おまかせ下さい!東大卒講師歴20年の図解講師「そうちゃ」が「約分」「通分」などの教え方を分かりやすく説明します。
小学6年生や分数を全部習い終わった中学受験生の方は「分数が苦手な小6への教え方」を御覧下さい。
目次(クリックでジャンプ)
まえがき
●分数学習の山場は実は○年生
こんにちは!「そうちゃ」@zky_tutor(プロフィール)です。
分数の学習について一番話題になるのは「分数の割り算が逆数のかけ算になる理由」次が「分数のかけ算のやり方」で、これらは小6で学習する内容です。
しかし、分数学習の山場は6年ではありません。
小学校の分数のカリキュラムを見てみましょう
| 2年 | 1学期 | |
| 2学期 | ||
| 3学期 | 1/2,1/4,1/8の意味 | |
| 3年 | 1学期 | |
| 2学期 | ||
| 3学期 | 真分数と足し算引き算,X/10と小数の関係 | |
| 4年 | 1学期 | |
| 2学期 | ||
| 3学期 | 帯分数と仮分数,分母が等しい分数の足し算引き算 | |
| 5年 | 1学期 | |
| 2学期 | 分数と小数、倍分と約分・通分、分母が異なる分数の足し算引き算 | |
| 3学期 | 分数と整数のかけ算・割り算 | |
| 6年 | 1学期 | 分数と分数のかけ算・割り算 |
| 2学期 | ||
| 3学期 |
これを見るとわかりますが、分数の学習の密度が一番高いのは小5ですね。
小5の2学期は通分と足し算・引き算、3学期がかけ算割り算、と内容がガラッと変わります。
そして、実は足し算ひき算の方が、かけ算わり算よりも難しいのです。
それなのに、しっかり復習定着させないまま3学期に進んでしまい、頭がごちゃごちゃになって6年生になった時に一気に分数が苦手になってしまう、というパターンが多いんです。
つまり分数学習の山場は「小5の2学期」なのですね!
従って、分数を苦手にしないためには小5の夏休みに予習したり小5の冬休みに復習して、足し算引き算までの内容をしっかり定着させておく必要があります。
そして短期に予習・復習する場合はコンパクトにポイントを絞って教えないといけません。
●学習内容のポイント
4年生で帯分数↔仮分数を、5年生で倍分・約分・通分を習います。これらは分数を様々な形に変身(変形)する操作ですね。
分数は計算方法を大幅に広げる道具。分数は計算が出来ることが大事。
従って、今回の学習内容のポイントは「計算に役立つように、分数を自在に変形できる」ことになります。
さらに、学習方法についても気を付けることがあります。
●教え方学び方のポイント
分数(に限りませんが)の学習方法のポイントは次の2つです。
❶スモールステップと定着期間
❷暗記・復習素材
❶スモールステップと定着期間
一気に教えると分からなくなって「分数嫌い!」となってしまう
教える内容を適当な大きさに分割して、その間に「定着期間」を作って教えます。
今回は次のような4ステップの間に定着期間を3つ挟んで全部で7段階で行います。
- 帯分数と仮分数
- 定着期間1
- 約分と倍分
- 定着期間2
- 通分
- 定着期間3
- 通分のある足し算引き算
全部のステップを行う場合は最短でも7日間はかけましょう。
❷復習素材を作る
そして習ったことをしっかりと定着させて後で復習できるように、カードのような復習素材にまとめておきましょう。
オススメは大型の暗記カード(ダイソーの大型方眼カード)です
カードを作る時は穴の位置に気をつけて下さい。
A4の紙を使って暗記プリントにしても良いでしょう。
真ん中より左寄りに区切り線を書き、左に問題・右に解答を書きます。裏は使わず表だけに書きます。
 爽茶
爽茶STEP1:帯分数↔仮分数
このステップは4年の復習です。まずお子さん・生徒さんにチェック問題を解いてもらいましょう。
カッコをタッチするか(スマホ)マウスポインタをあてると(パソコン)解答が表示されます。
(1)423を仮分数に直しなさい→(143)
(2)94を帯分数に直しなさい→(214)
お子さん・生徒さんが「パッ」とできたら、STEP1とSTEP1.5は必要ありません。2に飛んで下さい(全部で最短5日コース)。
パッとできなかった場合、カードを作りながら説明をしていきましょう。
まずカードの表(プリントの左半分)に問題を書きます。

注意:当サイトの画像を真似ながらカードを作る時は「穴の位置(左右どちらか)」をよく見て下さい。裏表を間違える確率が減ります。
次に、裏を書きながら説明します。ポイントは「分母は変わらない」ことです。

このSTEPは復習なので、色を付けながら「帯分数の分母と整数をかけ算した答えが仮分数の分子」「仮分数の分子÷分母の答えが帯分数の整数で余りが分子」という説明で十分でしょう。ゲーム感覚で楽しく解かせましょう
口頭の説明で理解できない場合は、教科書等を併用して詳しく説明するか、当ブログの「帯分数を(に)仮分数に(を)直す。分数の種類」を利用して下さい。
追加のカードを作る
理解できたら、練習問題として追加のカードを作ります。
カード2
カード3

表の問題を見て、ノート等に全部が正答できるようになったらSTEP1は終了です。
が、STEP2に行く前に…やることがあります。
STEP1.5:定着期間その1
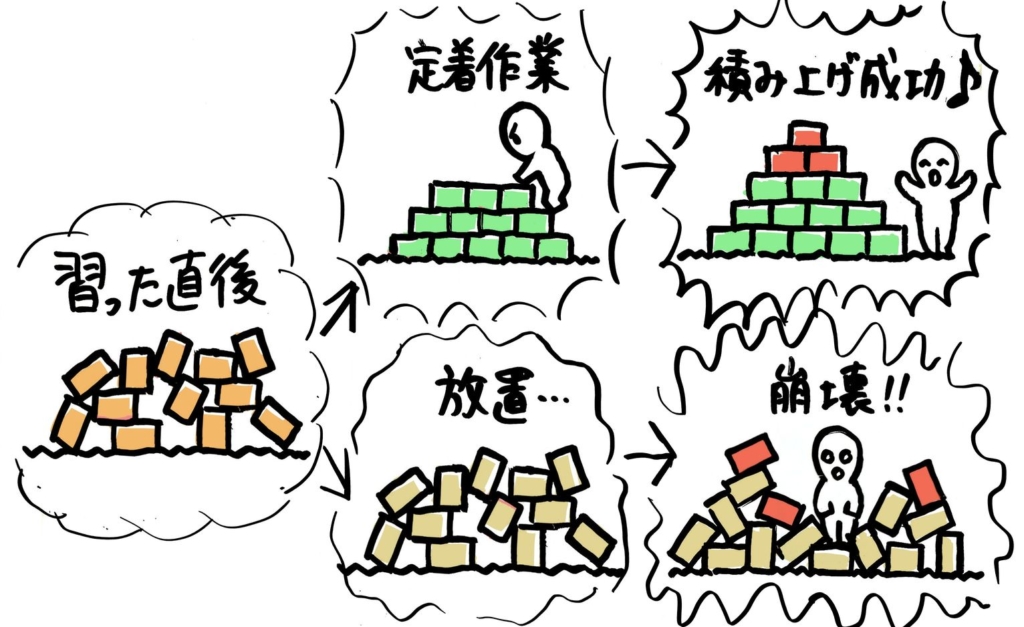
学習したら必ず定着のための期間を作ります。定着させる期間は得意な生徒でも半日、苦手な生徒なら1週間はとりましょう。
始めはカードの表を見て、途中過程も含めて裏と全く同じようにノートに書いて解けるようにします。
ノートに解けるようになったら、今度は口で言えるようにします。
例えば最初のカードなら、表の「➀423を仮分数にしなさい」を見て「3かける4たす2が14なので3分の14!」と言えるようにします。
これでSTEP1.5が終了です。
 爽茶
爽茶STEP2:倍分と約分
このステップから5年の内容に入ります。ここでは分子と分母に同じ操作(かけ算・割り算)をすることを体で覚えます。
倍分
1枚目のカードは「倍分」です。
カードの表に問題を書きます。

カードの裏を書きながら説明します。ポイントは分母と分子に同じかけ算をしないとダメということです。
さらに大事なのは、矢印で示した「3倍」などを実際に声に出させることです。分母・分子をともに3倍する場合は「3倍、3倍」と繰り返し声に出させます。
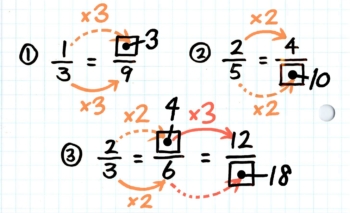
これを見ながら「2倍2倍」と唱える
カードができたら、生徒が表を見てノートに自力で正答できることを確認します。
約分
2枚めのカードは約分です。
カードの表を書きます

カードの裏を書きながら説明します。ポイントは「倍分」と同様に分母と分子に同じ作業をすることです。
この時も「÷3」などを実際に声に出させることが大事です。分母・分子をともに3で割る場合は「÷3、÷3」と繰り返し声に出させます。
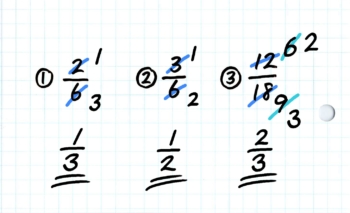
カードができたらノートに解かせて確認します。
ちなみに倍分と約分を組み合わせた問題がありますが、分数計算には必要ないので省略します。
興味がある人は当ブログの「約分・倍分」内の練習問題(コチラ)を練習すると良いでしょう。
さて、作った2枚のカードをノートに全部正答できるようになったらSTEP2も終了です。
STEP2.5定着期間その2
STEP1.5と同じ様に定着させます。
ここでは、STEP2で作ったカードだけでなく、STEP1で作ったカードも復習します。
ノートに解く→口で言えるようにする と進んで下さい。
 爽茶
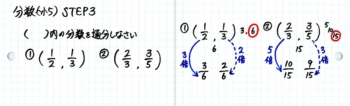
爽茶STEP3:通分
次は通分です。これが出来れば分数学習の山は超えたことになります。
カードの表に問題を書いて

やり方を説明しながら裏を書きます。
大きい方の分母を2倍・3倍した数を横に書いて、小さい方の分母の倍数にもなったら丸をつけます。これが分母の最小公倍数でした
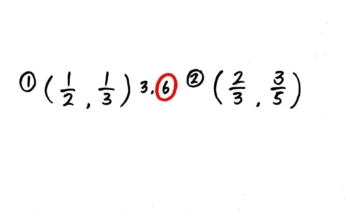
次に最小公倍数を分母にして分子は空白の分数を2つ並べて書きます。ここまでが通分の準備です。
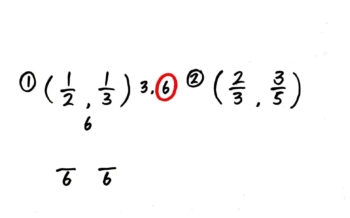
左の分数から、分母が何倍になっているか見て分子を同じだけ倍します。矢印の動きを指で辿らせながら「3倍,3倍」と声に出させて分子を3倍した3を書かせます。
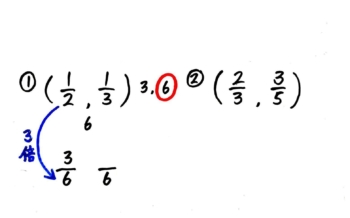
右の分数も同じように「2倍2倍」と声に出させて分子に2をかかせます。

②も同様に解いて、カードの裏を完成させます。
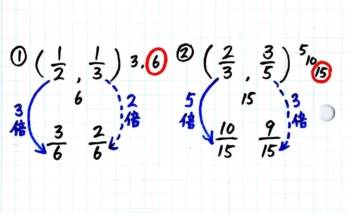
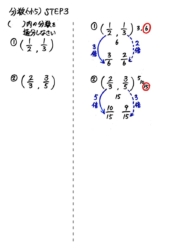
理解できたら、生徒が表を見て自力でノートに解けるか確認します。
正答できたら、2枚目のカードを追加します。
3つの分数の通分です。

やり方は同じです。一番大きな分母を2倍・3倍していって残り2つの分母の倍数になったら、その数(最小公倍数)に分母をそろえます。
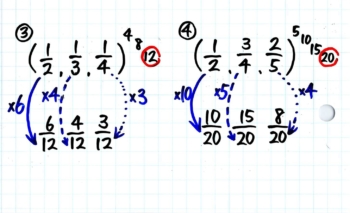
2枚目のカードをノートに解かせて全部正答できるようになったらSTEP2も終了です。
STEP3.5:定着期間その3
3回目の定着期間です。
STEP1,2,3で作ったカードをノートに解く→口で言えるようにする と進んで下さい。
学習事項が3つあるので、算数が苦手な子の場合「体が覚える」のに時間がかかることもあるでしょう。焦らずに繰り返して時間をかけて定着させましょう。
これで分数を自由自在に変形することが出来るようになったはずです。
 爽茶
爽茶STEP4:分数の足し算引き算
ゴールは通分のある分数の足し算引き算です。
1枚目のカードの表に問題を書きます。

説明しながら裏を書きます。
まずSTEP3でやったのと同じように分母の最小公倍数を考えて、分子が空白の分数を書いてしまいます。
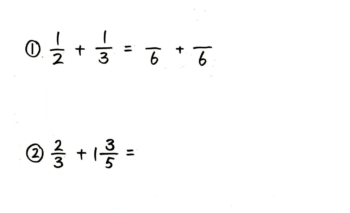
次に分母が何倍になっているかを見て、同じ倍率で分子を倍します。この時に「(分母)3倍,(分子)3倍」と声に出すとミスが減ります。
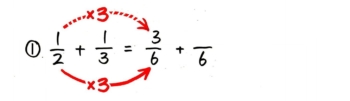
通分が終わったら分子の足し算をして終了です。

②も同じように通分・足し算をします。帯分数の整数部分は倍しないことに注意しましょう。
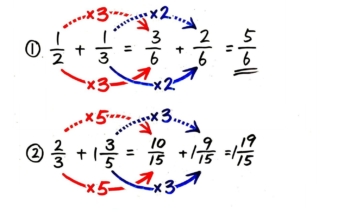
135の「1」は3倍しません。
最後に11915を2415に直して(分数の繰り上がり)終了です。
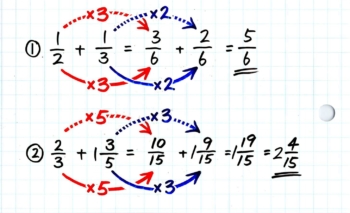
2枚目のカードを作ります。こちらは引き算です。
カードの表に問題を書き
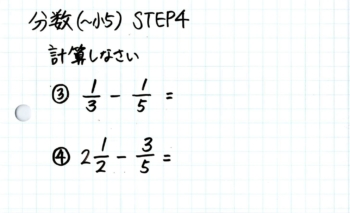
③は簡単ですね。
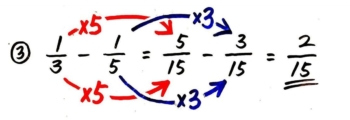
④は分数の「くり下がり」をします(*の部分)。
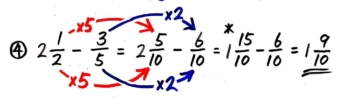
説明を書き加えました。

「くり上がり」や「くり下がり」に詳しい説明が必要な場合は、教科書やお持ちの参考書又は当ブログの「分母が異なる分数の足し算・引き算」を参照して下さい。
これで最後のカードも完成しました!!
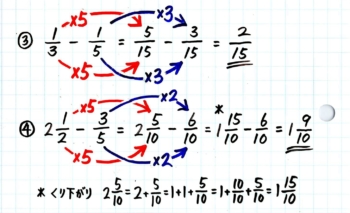
2枚のカードをノートに解かせて全部正答できるようになったらSTEP4も終了です。
翌日に全部のカードを復習して下さい。
分数が苦手で無くなりましたか?
 爽茶
爽茶お疲れ様でした!後は、手元に残ったカード・プリントを定期的に復習すれば忘れることはないでしょう。
「分数のまとめ」から他の記事や6年の予習に進んで下さい。