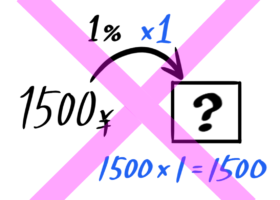「割合の単位って色々あって分かりづらい!」「パーセントと歩合を直す方法が分からない!」という小学生の方、確かに「%」「割」「分」など色々な言葉が出てきて頭がゴチャゴチャするかもしれません
でも安心して下さい。「%」の使い方が分かれば残りの単位も簡単に使えるようになりますよ♪
この記事では割合の単位「%」「割」「分」等を東大卒講師歴20年の図解講師「そうちゃ」が分かりやすく説明します
記事を読んで例題を解けば、割合の単位が出てきても自信を持って解けるでしょう♪
目次(クリックでジャンプ)
割合の基本(復習)
割合の意味
→あるモノが別のモノの「何倍」かを表した数
●矢印図
3つの数が「A×B=C」の関係にある時
矢印の向きに沿ってA,B,Cを並べた図
B(矢の数)が割合を示している
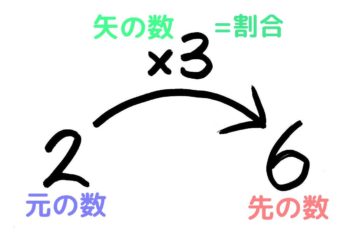
「2の3倍は6」
「6は2の3倍」

●矢印図による割合の公式
➊さきの数(6)=もとの数(2)×矢の数(3)
❷矢の数(3)=さきの数(6)÷もとの数(2)
❸もとの数(2)=さきの数(6)÷矢の数(3)
くわしくは関連記事「割合の基本」を見て下さい
割合の単位とは
上の矢印図で、割合を示す「矢の数」は「~倍」という表現になっています。
これを「~パーセント(%)」や「~割」で表現することがあります。
この「パーセント(%)」や「割」が割合の単位です。
つまり「~パーセント(%)」や「~割」を見て「これは『~倍』のことだね」と分かるようになればOK!ということです♪
パーセント(百分率)

 爽茶
爽茶こんにちは!「そうちゃ」@zky_tutor(プロフィール)です。
割合の単位には「パーセント」と「歩合(ぶあい)」があります。
最初に日常生活で一番よく使う「パーセント」を説明します。
パーセント(%)の意味
パーセントは、「全部」つまり「×1」を100とした表し方です。
もう少し分かりやすくいうと「100等分したうちの何個か」です(だから「百」「分」率なんですね。)
→あるものを100等分したうちのいくつか
「1%」→あるものを100等分したうちの一つ
「100%」→あるもの全体(×1と同じ)
「%」を「~倍」に直す
実は、パーセントはそのままでは「矢の数」として計算では使えません。
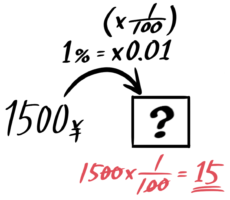
例えば1パーセントは100等分したうちの1個。つまり「×1100」や「×0.01」と同じ意味です。
ですから「1500円の1%」を求める時の矢の数は「1」ではなく「×1100」になるので「1500円×1100=15円」という計算になります。
同じように50パーセントは100等分したうちの50個なので「×50100(小数に直すと×0.5)」で「半分」と同じ意味で
「1500円の50%」は「1500円×50100=1500円×12」で750円になります。
さらに100パーセントは100等分したうちの100個なので「×100100(約分して×1)」で「全部」と同じ意味になります。
1%=×1100=×0.01
50%=×50100=×0.5=半分
100%=×100100=×1=全部
このように、%を矢の数として使う時は「÷100」つまり「分母を100にした分数」にして下さい。
(小数でも良いですが、分数の方が約分ができて計算は楽になりますよ。)
●「%」の分母に100をつける
「100%」→「×100100」-(約分)→「×1」
「200%」→「×200100」-(約分)→「×2」
「50%」→「×50100」-(約分)→「×12」
「50%」→「×50100」-(または)→「×0.5」
「25%」→「×25100」-(約分)→「×14」
「25%」→「×25100」-(または)→「×0.25」
「6%」→「×6100」-(約分)→「×350」
「25%」→「×25100」-(または)→「×0.06」
●「%」が小数なら分母に1000や10000を
「12.5%」→「×1251000」-(約分)→「×18」
「25%」→「×25100」-(または)→「×0.125」
「倍」を「%」に直す
反対に「~倍」を「~%」に直す場合はどうすればよいでしょうか?
上の例で「×1」=「100%」という例を書きました。数字だけに注目すると、「1」が「100」になっているので、ただの「倍」から「%」に直すには100倍すれば良いと分かります。
例えば「×2」は「200%」になります。
よくあるのは「×0.5」のような小数倍や「×12」のような分数倍をパーセントに直すことです。
「×0.5」は0.5を100倍して「50%」、「×12」も12×100=1×1002=1×501=50なので「×0.5」も「×12」も「50%」になります。
「倍」の数を100倍する
「×1」-(100倍)→「100%」
「×2」-(100倍)→「200%」
「×0.5」-(100倍)→「50%」
「×1.43」-(100倍)→「143%」
「×12」-(100倍)→「50%」
「×920」-(100倍)→「45%」
こうして見ると、わざわざ「パーセント」を作った理由が分かりませんか?
0.5や12のような小数・分数よりも50という整数の方が分かりやすいからですね。
確認テストをどうぞ
確認テスト(タッチで解答表示)
5%→( 5100=120倍 または 0.05倍 )
40%→( 40100=25倍 または 0.4倍 )
75%→( 75100=34倍 または 0.75倍 )
4.5%→( 451000=9200倍 または 0.045倍 )
0.3倍→( 30% )
1.7倍→( 170% )
14倍→( 14×100=25% )
320倍→( 320×100=15% )
パーセントが分かれば次は簡単です。
歩合(ぶあい)
「~割」とか「~割~分」というのを聞くと思いますが、あれが「歩合」です。別に難しくありませんよ!
歩合は三種類
大きい順に「割」「分」「厘」の三種類があります。
割(わり)
まず、「割」というのは「全体を10等分したうちの何個か」という意味です。
例えば「1割」は10等分したうちの1個。つまり「×110」や「×0.1」と同じ意味です。
「5割」は10等分したうちの5個なので「×510(小数に直すと×0.5)」で「半分」と同じ意味
「10割」は10等分したうちの10個なので「×1010(約分して×1)」で「全部」と同じ意味になります。
分(ぶ)
次に「分」は「全体を100等分したうちの何個か」という意味です。つまりパーセントと全く同じです!(「分」は昔から日本で使われていて、そこに外国から「%」が入ってきました)
「1分」は100等分したうちの1個。つまり「×1100」や「×0.01」と同じ意味です。
「3分」は100等分したうちの3個なので「×3100(小数に直すと×0.03)」と同じ意味
「10分」は100等分したうちの10個なので「×10100(約分して×0.1)」と同じ意味になります。
気づいた人もいるでしょうが、「10分」は「×0.1」なので「1割」と同じ意味になります。だからピッタリ「10分」の場合は「10分」と言わずに「1割」と言います。同じように「30分」は「3割」、「50分」は「5割」、「80分」は「8割」と言います。
一方、半端な場合たとえば「15分」のような場合は「1割5分」のように「割」と「分」が混ざった言い方になります。パーセントを使うと「15%」でこちらは単純ですね。
厘(りん)
最後の「厘」は1000等分した割合で、「1厘」が「×11000」や「×0.001」と同じ意味です。「10厘」は「×101000(約分して×0.01)」なので「1分」と同じ意味になり、例えば「15厘」は「1分5厘」と言います。
歩合をパーセントや小数/分数に直す
単位が3つもあるので、ちょっと混乱しましたね。
歩合も%同様そのままでは計算には使えず、「~倍」に直さないといけません
そこで「1分」=「1%」を利用して歩合を%に、ついでにパーセントから~倍に直してみましょう。
●基本ルール
1割=10%=10100=×0.1
1分=1%=1100=×0.01
1厘=0.1%=101000=×0.01
(例)
4厘3分2割=.420%=20100=×0.2
4厘2割3分=.423%=23100=×0.23
2割3分4厘=23.4%=2341000=×0.234
これで歩合を矢の数字として使えるようになります。
%を歩合に直して整理
反対に%を歩合にしてみましょう。
ポイントは%の一の位を「分」にして、それより上は「割」下は「厘」にすることです。
→%の一の位を「分」にする
1割=10%、1分=1%、1厘=0.1%
23% =
23.4%=
2割3分
2割3分4厘
120% =
123% =
123.4%=
12割
12割3分
12割3分4厘
100%より上は「割」が10より大きい数字になることに注意しましょう!
確認テストをどうぞ
(2021.7.8作成中)
単位の相互変換まとめ
割合を表す数字と単位が「整数・小数」「分数」「%」「歩合」と4種類でてきました。さっきの「歩合をパーセントに直す」にもまとまっていますが、テキストにあるように「整数・小数」から順に表にまとめるとこうなります。
| 整数・小数 | 分数 | パーセント | 歩合 |
| ×1 | ×100100 | 100% | 10割 |
| ×0.5 | ×510(12)=50100 | 50% | 5割 |
| ×0.03 | ×3100 | 3% | 3分 |
| ×0.25 | ×25100(14) | 25% | 2割5分 |
| ×0.253 | ×2531000 | 25.3% | 2割5分3厘 |
| ×1.253 | ×12531000 | 125.3% | 12割5分3厘 |
こうしてみると、パーセントが単純で分かりやすく便利と分かりますね。
単位を直すのは割合の問題を解くときの最初の作業ですのでサクッと出来ることが必要です。確認テストをどうぞ
空欄を埋めなさい
| 整数・小数 | 分数 | パーセント | 歩合 |
| ×0.3 | ×310=30100 | 30% | 3割 |
| ×0.07 | ×7100 | 7% | 7分 |
| ×0.05 | ×5100(120) | 5% | 5分 |
| ×0.41 | ×41100 | 41% | 4割1分 |
| ×0.75 | ×75100(34) | 75% | 7割5分 |
| ×0.253 | ×2531000 | 25.3% | 2割5分3厘 |
| ×0.375 | ×3751000(38) | 37.5% | 3割7分5厘 |
| ×1.253 | ×12531000 | 125.3% | 12割5分3厘 |
「増し」と「引き」
「~%増し」とか「~割引き」と聞いたことはありますね(「消費税は10%増し」など)?
難しい話ではありません。気楽に読んで下さい♪
一番大事なこと
一番大事なのは、「増し」「引き」をすると、「先の数」が「元の数」よりも大きくなるか、小さくなるかを間違えないことです。
「~増し」はもとの数より大きくなります。矢印図が「小→大」になります。
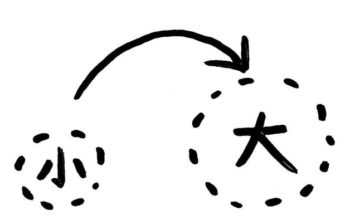
ということは、かける数(矢の数=割合)は1(100%)(10割)より大きいはずです。これを頭に入れて図を書き、計算すれば間違えません。
「~引き」はもとの数より小さくなります。矢印図が「大→小」になります。
ということは、矢の数は1(100%)(10割)より小さいハズですね。
このように、大きくなるか小さくなるかをハッキリとイメージできれば正しい答えが出せますよ!
では、「増し」「引き」それぞれの場合を見ていきます。
「増し」=もとの数より大きくなる
「増し」の前には「10%」「3割」などの言葉がついていましたね?これが「どれくらい大きくなるか」を表しています。例えば「10%増し」なら「もとの数より10%大きくなる」という意味です。
百分率でもとの数は「100%」でしたから「10%増し」は「もとの数の100%+10 %」=「もとの数の110%」つまり「×1.1」になります。(ちなみに一番多いミスは「10%増し」を「10%」と同じに考えて「×0.1」としてしまうパターンです。「増し」はもとの数より大きくなるのを忘れないように!)
同じように「3割増し」ならもとの数(10割)より3割大きくなるので「もとの数の10割+3 割」=「もとの数の13割」つまり「×1.3」になります。(これも×0.3としないように注意して下さい)
ただ、歩合は「割」「分」「厘」と単位が3つもあるので%に直してしまう方がやさしいでしょう(1割=10%、1分=1%、1厘=0.1%)。例えば「3割2分増し」なら3割2分=32%なので「32%増し」と考えて「100+32=132%」=×1.32とします。(歩合とパーセントに直すのが不安な人は上を復習して下さい)
まとめるとこうなります。
→もとの数(100%、10割)に加える
(例)10%増し
=100%+10%=110%=もとの数×1.1
(例)3割増し
=(10割+3割=13割=もとの数×1.3
または=30%増し=130%=もとの数×1.3
(例)3割2分増し
=32%増し=(100+32)%=132%=×1.32
「引き」=もとの数より小さくなる
「引き」は「増し」の反対です。
例えば「10%引き」なら「もとの数(100%)より10%小さくなる」という意味で、つまり「もとの数の100-10=90%」つまり「×0.9」になります。
歩合は%に直します。「3割引き」なら「30%引き」なので「もとの数の100-30=70%」つまり「×0.7」に、「3割2分引き」なら3割2分=32%なので「100ー32=68%」=×0.68とします。
まとめると、こうなります。
→もとの数(100%、10割)から引く
(例)10%引き
=100%ー10%=90%=×0.9
(例)3割引き
=10割-3割=7割=×0.7
または=30%引き=70%=×0.7
(例)3割2分引き
=32%引き=100%ー32%=68%=×0.68
増し引きの確認
確認テストをどうぞ
13%増し→( 113%なので×1.13 )
4割増し→( 40%増し=140%なので×1.4 )
1割9分増し→( 19%増し=119%なので×1.19 )
7%引き→( 93%なので×0.93 )
2割引き→( 20%引き=80%なので×0.8 )
3割3分引き→( 33%引き=67%なので×0.67 )
 爽茶
爽茶オリジナル教材のご案内
御三家・早慶付属など難関・人気の中学に合格した2025年度の受験生達から大好評!
分かりやすいのはもちろん、スキマ時間にお子様一人で反復定着できますよ
人気教材はこちら(クリックするとショップ内教材ページにジャンプ)
●歴史 ●時事問題(2025年) ●世界地図 ●世界遺産
■仕事ニュートン算 ■食塩水 ■売買損益
★月の形 ★電流 ★水溶液/気体の性質
その他にも社会/理科/算数の教材がございます。興味がある方は公式ストアへどうぞ