「割合の文章問題が苦手…」という小5の方へ。確かにいろんな用語や数字が出てきて頭がゴチャゴチャするかもしれません。
しかし安心して下さい。「ある図」を使えば割合の問題は全部同じようにとけてしまうのです！
この記事では東大卒講師歴20年の図解講師「そうちゃ」が「矢印図」を使った文章題の解き方を分かりやすく説明します。
記事を真似して例題を解けば、割合の文章題に自信をもって向き合えるようになるでしょう♪
目次(クリックでジャンプ)
割合の計算方法(復習)
爽茶文章問題を解くのに使う図と計算を簡単に復習します。
●矢印図
3つの数が「A×B=C」の関係にある時
矢印の向きに沿ってA,B,Cを並べた図
B(矢の数)が割合を示している
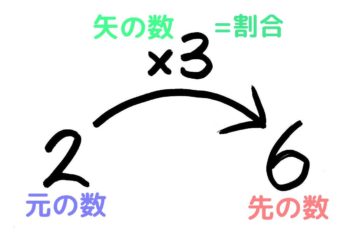
「2の3倍は6」
「6は２の3倍」
●矢印図による割合の公式
➊さきの数(6)=もとの数(2)×矢の数(3)
❷矢の数(3)=さきの数(6)÷もとの数(2)
❸もとの数(2)=さきの数(6)÷矢の数(3)
この「矢印図」を使えば、文章題から簡単に式を作ることができます。
また割合の単位を「～倍」に直す方法も思い出してください
「%」の分母に100をつけると「倍」に戻る
「100%」→「×100100」－(約分)→「×1」
「200%」→「×200100」－(約分)→「×2」
「50%」→「×50100」－(約分)→「×12」
「50%」→「×50100」－(または)→「×0.5」
●基本ルール
1割=10%=10100=×0.1
1分＝1%=1100=×0.01
1厘＝0.1％=101000=×0.01
(例)
4厘3分2割=.420%＝20100=×0.2
4厘2割3分＝.423％＝23100＝×0.23
2割3分4厘＝23.4％＝2341000＝×0.234
「～増し」や「～引き」を「～倍」に直す方法はこうでしたね。
→もとの数(100%、10割)に加える
(例)10%増し
=100%+10%=110%=もとの数×1.1
(例)3割増し
=(10割+3割=13割=もとの数×1.3
または=30％増し=130%=もとの数×1.3
(例)3割2分増し
=32%増し=(100+32)%=132%=×1.32
→もとの数(100%、10割)から引く
(例)10%引き
=100%ー10%=90%=×0.9
(例)3割引き
=10割-3割=7割=×0.7
または=30%引き=70%=×0.7
(例)3割2分引き
=32%引き=100%ー32%=68%=×0.68
以上が「よく分からない」という人は関連記事「割合の基本と求め方」を見ると良いかもしれません。
それではさっそく文章題を解いてみましょう。
通常の割合の文章題
●例題6-(1)
「●×◯＝◎」の形にして矢印図を書き、それからゆっくり考えましょう。
「学校全体はAさんのクラスの22倍」を「2×3=6」の形に直すと、「Aさんのクラス(34人)×22倍=学校全体(?人)」つまり「34×22=？」になります。図にすると、こんな感じです。
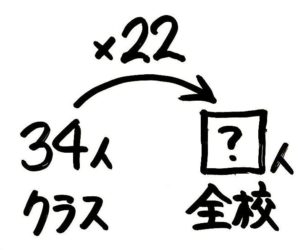
これで、?=34×22=748人と分かります。(このような「先の数」を出す問題は図を書かなくても分かる人も多いでしょう。)
答: 748人
●例題6-(2)
「～にあたる」の意味を思い出しましょう。思い出せなくても、とりあえず答えを出してみましょう。
「～にあたる」は「～倍である」と同じなので、「男子の人数がクラス全体の47にあたる」は「男子の人数がクラス全体の47倍」と同じで、いつもの形に直すと「クラスの人数(35人)×47=男子の人数(?人)」です。
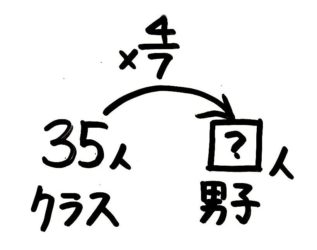
これで？=35×47=35×41×7=5×41×1=20人と分かります(この問題も図を書かなくても分かった人が多いでしょう。)
答: 20人
この調子でどんどんいきましょう♪
●例題6-(3)
計算する時、%の数字は…でした。
百分率(%)や歩合(割・分・厘)は、計算する時は小数倍か分数倍に直しましたね。
80%は小数倍にすると×0.8、分数倍にすると×80100=×45になるので、このどちらかを使います(分数の方が約分できるので簡単な計算になることが多いです)
これを使って問題の文章をいつもの形にすると「エレベータ定員の80%が乗っている人数」「定員(15人)×45=乗っている人数(?人)」になるので図はこうなります。
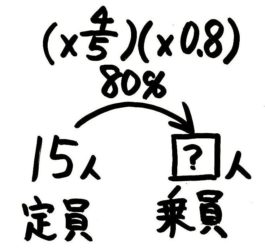
？＝15×45(または×0.8)=15×41×5=3×41×1=12人と分かります。
答: 12人
ここまでは「先の数(くらべる量)」を求める問題でした。次は…
●例題6-(4)
◯数だと答えが出ないので●数を使います。
クラス全員の人数が「もと」つまり「元の数」と分かるので、問題文の数字をいつもの順に並べると「36×？=12」です。これを図にして矢の数「？」の出し方を思い出します。
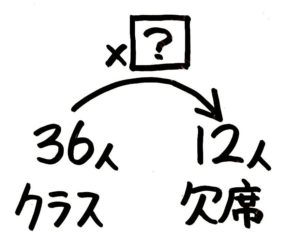
もし「36÷12」か「12÷36」か迷った場合には横に基本図である「2×3=6」を書いて…
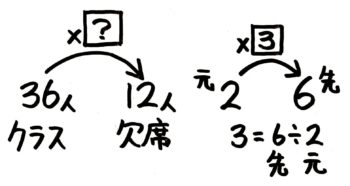
となりの「2×3=6」を見る
「矢の数=先÷元」を思い出せればOKです。
さて、先÷元の計算をすると…12÷36は0.33…となってしまい割り切れません。困りました。
そういう時は分数を使います。分数は分子÷分母の割り算と同じ意味なので、12÷36=1236=13が答えになります。
答: 13
この場合に限らず、整数÷整数は分数に直すのをオススメします。
●例題6-(5)
まず…を出してから歩合に直しましょう。
歩合は計算では直接求められないので、割合(矢の数)を出して歩合に直します。
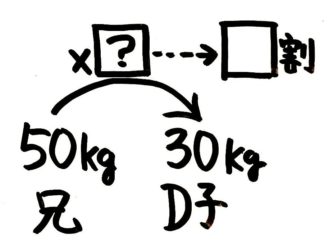
割合?=30÷50=3050=35=3÷5=0.6 で、これを歩合に直して、6割が答えです。
答: 6割
●例題6-(6)
この場合も%(百分率)を出すのは最後です。
図がこうなるのは分かるでしょう。
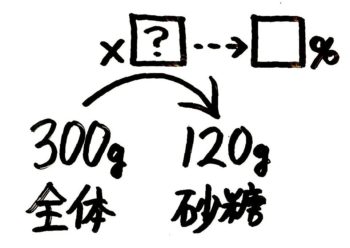
120÷300=120300=25=2÷5=0.4で、これを%に直した40%が答えです。
答: 40%
ここまでは「矢の数(割合)」を出す問題でした。次は…分かりますね。
●例題6-(7)
矢印図をバージョンアップさせると良いかもしれません。
図を書くと元の数を出す問題と分かります(➀)。式をすぐ思いつかないなら反対向きの矢印を書きます(➁)。
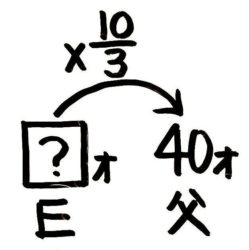
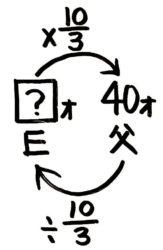
これで、？=40÷103＝40×310=40×31×10=12と分かります。
答: 12歳
●例題6-(8)
歩合(8割5分)を計算に使う形に直しましょう。
8割5分=85%=×0.85を使って図を書き、必要なら反対向きの矢印を付け足します。
これで、?=34000÷0.85=40000と求められますね
答: 40000円
●例題6-(9)
同じように解きます。
33%=×0.33に直して図を書けば計算方法も分かりますね。
？=231÷0.33=700ですね。
答: 700人
増し引きの文章題
次は「増し」「引き」の文章題です。これができれば基本的な文章問題は大丈夫です！
「増し」「引き」の基本が不安な人は上の方にある「割合の増しと引き」を見直してからチャレンジして下さい。
●例題7-(1)
「2割増し」を計算で使える数字に直しましょう。
「2割増し」＝10+2=「12割」=×1.2 に直して計算すると、15×1.2=18 と分かります。
答: 18個
？=15×1.2=18
●例題7-(2)
「18%引き」を計算で使える数字に直しましょう。
「18%引き」=100-18=「82%」=「×0.82」になおして計算すると、6000×82=4920円と分かります。
答: 4920円
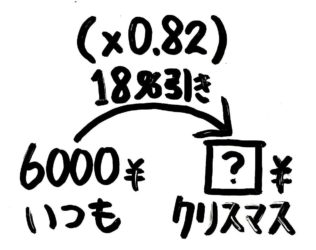
?=6000×0.82=4920
●例題7-(3)
百分率(%)や歩合(割・分・厘)そのものは計算では出せません。
去年(620)を元の数にして今年(651)の割合を求めると、651÷620=1.05倍。これを％に直すと105%になる。105=100+5なので5%増しと分かる。
答: 5%増し
?=651÷620=1.05→105%=5%増し
●例題7-(4)
今までの知識を総動員して解いて下さい。
まず「3割引き」を分数倍(小数倍)に直すと「×710(×0.7)」なので「定価(？)×710＝売値(490)」と分かるので図を書きます(➀)。元の数を求めるので、逆向きの矢印を書き加える(➁)と分かりやすいですね。
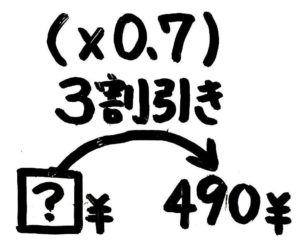
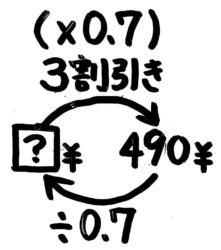
定価(?)＝490÷710=＝490×107=490×101×7=70×101×1=700円と求められる。
答: 700円
爽茶もっと問題を解きたい人は「毎日のドリル」シリーズのような市販の分野別問題集も良いでしょう。
歴史を学習する小学生の保護者の方へ
年表,年号,地図,書き取りテストなど400枚のプリントがセットになったそうちゃ式オリジナル教材が8/25(日)までお買い得価格！興味がある方はコチラへ
2023年度生徒さん募集
2023年度の生徒さんの募集を開始しました(対面授業の一次募集)
東武野田線・伊勢崎線沿線にお住まいの新5年生で予習シリーズをベースにされている方が対象です。
詳しくはコチラのページを御覧下さい
新4年生の方を対象に学習相談/授業を実施します(2次募集はサピックス新越谷校・南浦和校の方のみ対象。締め切り1/27)。応募はコチラから
中学受験でお悩みの方へ
爽茶「中学受験と高校受験とどちらがいいの？」「塾の選び方は？」「4年次・5年次はどう勉強すればよい？」「志望校の過去問が出来ない…」など
様々なお悩みへのアドバイスをまとめたので参考にして下さい。
もしかしたら、自分だけで悩んでいると煮詰まってしまい、事態が改善できないかもしれません。講師経験20年の「そうちゃ」に相談してみませんか？対面/オンラインの学習相談を受け付けているので、ご利用下さい。