小学4年生】四捨五入のやり方と問題【無料プリントで小数点も分かりやすい

「四捨五入の問題の解き方が分からない」と悩んでいる小学4年の方、もう大丈夫ですよ！東大卒講師歴20年の図解講師「そうちゃ」が分かりやすく教えます♪きっと四捨五入が得意になりますよ。

下の目次で読みたい箇所をクリックするとジャンプできます。記事の最後ではプリントがダウンロードできますよ。

目次(クリックでジャンプ)

切り捨て切り上げ(復習)

四捨五入の前に「切り捨て」「切り上げ」を軽く復習です。

切り捨て・切り上げの問題は❶まず切り捨てた数を出して❷次に切り捨てた数から切り上げた数を出します。いきなり切り上げを求めようとしないのが大事です。

❶切り捨てには問題文の聞き方によって三種類の方法があります。

❶問題文と切り捨ての方法

A「～の位を切り捨て(上げ)なさい」
→その位からゼロにする
(例)1234を十の位で切り捨て→1200

B「～の位までの概数にしなさい」
→一つ下の位からゼロにする
(例)1234を十の位までの概数に→1230

C「上から～ケタの概数にしなさい」
→上から+1ケタからゼロにする
(例)1234を上から2ケタの概数に→1200

❷切り捨てた数から切り上げた数を求めるやり方は問題文の聞き方と関係なくいつも同じで「ゼロにした部分より左(上)の数字を1つ進める」です。

(例)
切り捨てた数が230→切り上げると240
切り捨てた数が12300→切り上げると12400
切り捨てた数が99000→切り上げると100000

では、四捨五入に進みましょう。

やり方の前に…「四捨五入」って何？

爽茶そうちゃ

こんにちは！「そうちゃ」@zky_tutor(プロフィール)です。

まず、四捨五入の意味をキチンと理解しましょう。
「問題を解きたい！」という人はジャンプして下さい。

ちょうど○○だったらどうするの？

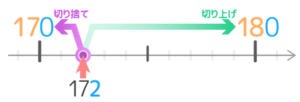
172を一の位で切り捨てると170、切り上げると180になります。

172を一の位での切り捨て・切り上げ

これって、どちらが適切でしょうか？もちろん両方とも正確ではないんですが、どちらがより正確でしょうか？

矢印の長さを見ると紫の「切り捨て」の方が短いので、切り捨ての方がもとの値に近くてより正確ですね。

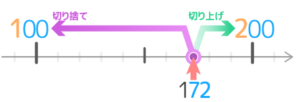
では、172を十の位で切り捨て・切り上げるとどうでしょうか？切り捨ては100、切り上げは200になります。

172を十の位での切り捨て・切り上げ

今度は緑の「切り上げ」の方が短いですので、切り上げの方が適切ですね。

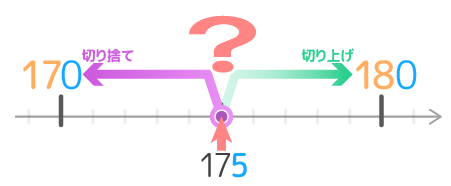
ここまでを整理すると、切り捨てた数と切り上げた数の真ん中の数を考えて、もとの数が真ん中より下なら切り下げ、真ん中より上なら切り上げをするのが自然で良いと分かります。

切り捨てる場合

172が真ん中(175)よりも
左にある(小さい)ので
切り捨て

⇔

切り上げる場合

172が真ん中(100)よりも右にある(大きい)ので
切り上げ

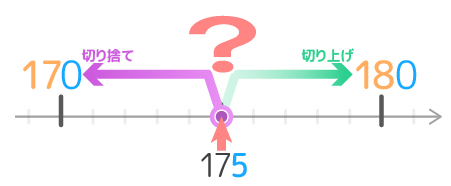
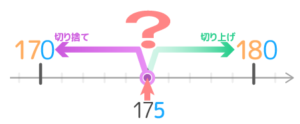
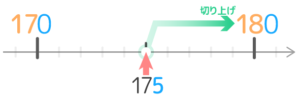
では、175を一の位で切り捨て切り上げするように、元の数が切り捨てた数と切り上げた数のちょうど真ん中にある場合は切り上げと切り捨てどちらにするのが良いでしょうか？

175は切り捨てるか切り上げるか？

真ん中は切り○げ

ちょうど真ん中なので、差を取っても175-170=5 と180-175=5 で同じになるので、どちらにしても良い気がします

しかし！これを各人の自由にしてしまうと、同じ175という数字を170とする人と180とする人が出てしまいます。確かに、この場合は差はたった10ですが、これが175万円だったら170万円と180万円で10万の差になってしまいますね！さらに百人千人単位でバラバラに集計したりしたら、不都合や不公平になって皆が困ってしまいます。

したがって、目盛りの真ん中の数は切り捨てるべきか、切り上げるべきか統一したルールを作ったほうが良いというわけで、「真ん中は切り上げる」というルールが出来てきたのです。(いつ、どこで、出来たのかは良く分かりませんが、5000年くらい前からあったらしいですよ！)

この「真ん中は切り上げる」というルールを「四捨五入」と呼ぶのです。

四捨五入の「意味」

●ある数(A)の切り捨てた数(X)と切り上げた数(Y)を出す

●XとYの真ん中の数(Z)を考える

●Aが┌Zより下→切り捨てXになる(➀)
●Aが┼Zより上→切り上げYになる(➁)
●Aが└Zと同じ→切り上げYになる(③)

((図①))((図②))((図③))

爽茶そうちゃ

次は、問題形式で解いてみましょう！

四捨五入は4ステップで

上で使ったのと同じ数字を実際の問題形式で解いてみます。誘導にそって答えて下さい！

1:

172を一の位で四捨五入しなさい。以下の問いに答えなさい。

方針

四捨五入の問題は4ステップで解きます。

解説

❶まず問題の数を切り捨てた数を出します。
172を「一の位で切り捨て」ると一の位をゼロにするので170です。

❷次に切り捨てた数から切り上げた数を出します。
切り捨てた170のゼロにした部分(0)の右(17)を+1して180です。

❸次に切り捨てた数と切り上げた数のちょうど真ん中にある数を出します。
切り捨てた数170と切り上げた数180のちょうど「真ん中」は175です。

❹最後に「四捨五入」を行います。
問題の数が真ん中の数未満(より小さい)なら切り捨て、真ん中の数以上なら切り上げです。
この問題で「聞かれている数」172は「真ん中の数」175未満(より小さい)なので切り捨てます。

170

今の解き方をまとめるとこうなります。

四捨五入の「解き方」

「問題の数」を「切り捨てた数」を出す
「切り捨てた数」から「切り上げた数」を出す。
「切り捨てた数」と「切り上げた数」の「真ん中の数」を出す
「問題の数」が「真ん中」未満(下)なら切り捨て、「真ん中」以上なら切り上げ。

実際の問題では概数の聞かれ方が三種類あるので四捨五入の解き方も三種類あります。

がい数の問題の種類

A「～の位を切り捨て(上げ)なさい」

B「～の位までの概数にしなさい」

C「上から～ケタの概数にしなさい」

この後、種類別に練習をしますが、解き方が変わるのはステップ①「切り捨て」だけで、ステップ②③④は同じなので安心して下さい♪

三種類の「四捨五入」

「問題の数」を「切り捨てた数」を出すAタイプ:「～の位を」Bタイプ:「～の位までの」Cタイプ:「上から～ケタ」
「切り捨てた数」から「切り上げた数」を出す。
「切り捨てた数」と「切り上げた数」の「真ん中の数」を出す
「問題の数」が「真ん中」未満(下)なら「切り捨てた数」、「真ん中」以上なら「切り上げた数」が答え。

Aタイプ(～の位を四捨五入)

「～の位を四捨五入」と聞かれた場合は、指定された位(から右)をゼロにすれば切り捨てた数が出ます。

「Aタイプ」の四捨五入の解き方

「問題の数」の指定された位から右をゼロにして「切り捨てた数」を出す
「切り捨てた数」から「切り上げた数」を出す。
「切り捨てた数」と「切り上げた数」の「真ん中の数」を出す
「問題の数」が「真ん中」未満(下)なら切り捨て、「真ん中」以上なら切り上げ。

1A-1:

172を十の位で四捨五入しなさい。以下の問いに答えなさい。

ヒント

4ステップで解いて下さい。

解説

❶172を「十の位で切り捨てた数」は100ですね。

❷「切り上げた数」はゼロにした部分より左の数字を+1して200です。

❸切り捨てた数100と切り上げた数200の「真ん中の数」は150です。

❹「問題の数」172は「真ん中の数」150以上なので切り上げます。

200

小数の四捨五入もやってみましょう！

1A-2:

1.72を小数第二位で四捨五入しなさい。以下の問いに答えなさい。

ヒント

答える時に注意して下さい。

解説

❶「小数第二位」で四捨五入なので、切り捨てた数は1.70です。

❷「切り上げた数」はゼロにした部分の左の数字を+1します。ここでは「1.7」ではなく「17」に+1すると考えて「18」にします。すると「切り上げた数」は1.80になります。

❸切り捨てた数1.70と切り上げた数1.80の「真ん中の数」は1.75です。

❹「問題の数」1.72は「真ん中の数」1.75より下(未満)なので切り捨てます。

1.7

Bタイプ(～の位までの概数)

Bタイプ(とCタイプ)は指定の位とゼロにする位が違うことに注意しましょう。

「四捨五入して～の位までの概数に」と聞かれた場合、ひとつ下の位からゼロにすれば切り捨てた数が出ます。

「Bタイプ」の四捨五入の解き方

「問題の数」の指定より一つ下の位から右をゼロにして「切り捨てた数」を出す
「切り捨てた数」から「切り上げた数」を出す。
「切り捨てた数」と「切り上げた数」の「真ん中の数」を出す
「問題の数」が「真ん中」未満(下)なら切り捨て、「真ん中」以上なら切り上げ。

1B-1:

1724を四捨五入して百の位までの概数にしなさい。以下の問いに答えなさい。

解説

❶切り捨てて「百の位までの概数」にするには、百の一つ下の十の位からゼロにします。

「問題の数」1724の場合、「切り捨てた数」は1700です。

❷切り捨てた数1700のゼロにした部分より左の数字17を1つ進めると「切り上げた数」1800になります。

❸「切り捨てた数」1700と「切り上げた数」1800の「真ん中の数」は1750です。

❹「問題の数」1724は「真ん中の数」1750より小さい(未満)ので切り捨てます。

1700

1B-2:

17.25を四捨五入して小数第一位までの概数にしなさい。以下の問いに答えなさい。

解説

❶「小数第一位までの概数」にするには一つ下の小数第二位をゼロにします。「切り捨てた数」は17.20です。

❷「切り上げた数」はゼロにした部分の左の数字「172」を+1して17.30になります。

❷「切り捨てた数」17.20と「切り上げた数」17.30の「真ん中の数」は17.25です。

❸「問題の数」17.25はちょうど「真ん中の数」17.25と同じです！真ん中は切り上げです。

17.3

Cタイプ(上から～ケタのがい数)

「四捨五入して上から～ケタの概数に」と聞かれた場合、上から+1ケタからゼロにすれば切り捨てた数が出ます。

「Cタイプ」の四捨五入の解き方

「問題の数」の指定+1ケタから右をゼロにして「切り捨てた数」を出す
「切り捨てた数」から「切り上げた数」を出す。
「切り捨てた数」と「切り上げた数」の「真ん中の数」を出す
「問題の数」が「真ん中」未満(下)なら切り捨て、「真ん中」以上なら切り上げ。

1C-1:

1724を四捨五入して上から1ケタの概数にしなさい。以下の問いに答えなさい。

解説

❶切り捨てて上から1ケタの概数にするには、上から2ケタ目からゼロにするので、切り捨てた数は1000です。

❷ゼロにした部分の左の数字を+1して「切り上げた数」は2000になります。

❸「切り捨てた数」1000と「切り上げた数」2000の「真ん中の数」は1500です。

❹「問題の数」1724は「真ん中の数」1500以上なので切り上げます。

2000

1C-2:

17.24を四捨五入して上から2ケタの概数にしなさい。以下の問いに答えなさい。

ヒント

答える時に気をつけましょう。

解説

❶切り捨てて上から2ケタの概数にするには、上から3ケタ目からゼロにするので、切り捨てた数は17.00です。

❷ゼロにした部分の左の数字を+1して「切り上げた数」は18.00になります。

❸「切り捨てた数」17.00と「切り上げた数」18.00の「真ん中の数」は17.5です。

❹「問題の数」17.24は「真ん中の数」17.5未満なので切り捨てます。
切り捨てた数は17.00ですが答える時は17に直します。

爽茶そうちゃ

これでABCの3タイプの四捨五入の問題が終了しました。四捨五入の問題は以上です。お疲れ様でした！

プリントダウンロード

四捨五入(問題)

四捨五入(解説)

爽茶そうちゃ

次はがい数の総合案内から応用問題へ進んで下さい。

もっと問題を解きたい人は市販の問題集を使うのも良いでしょう。算数が苦手な人には「陰山メソッド徹底反復およそのかずプリント」、中学受験の4・5年生には「算数の基本問題(日能研)」(5年用)が、中学受験の6年生には「算数ベストチェック(日能研)」が良いでしょう。

オリジナル教材のご案内

御三家・早慶付属など難関・人気の中学に合格した2025年度の受験生達から大好評！
分かりやすいのはもちろん、スキマ時間にお子様一人で反復定着できますよ

人気教材はこちら(クリックするとショップ内教材ページにジャンプ)
●歴史　●時事問題(2025年)　●世界地図　●世界遺産
■仕事ニュートン算　■食塩水　■売買損益
★月の形　★電流　★水溶液/気体の性質

その他にも社会/理科/算数の教材がございます。興味がある方は公式ストアへどうぞ