「概数の基本は分かったので応用問題が解きたい」という小4・中学受験生の方、お待たせしました！東大卒講師歴20年の図解講師「そうちゃ」が「概数の復元問題」を教えます♪記事を真似すれば得意になりますよ。
「復元問題」は小4の教科書にも載っていますが、実は結構レベルが高い問題です。概数の基本事項に自信が無い場合は関連記事「四捨五入」を先に見て下さい。
記事の最後でプリントがダウンロードできます。目次をクリックしてジャンプして下さい。
プリントに誤植がございます。
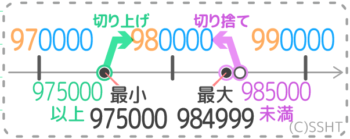
大問4の(3) 誤「最大は985999」 正「～984999」
twitterで「たくあん@2023中学受験」様よりご指摘いただきました。ありがとうございました。
目次(クリックでジャンプ)
概数(範囲)を復元する問題
(直接指定方式)
爽茶こんにちは！「そうちゃ」@zky_tutor(プロフィール)です。
今まで、色々な数を概数にしてきました。しかし反対に、ある概数になる整数は一つとは限りません。
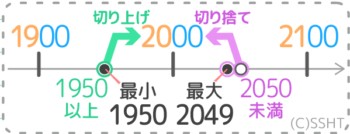
例えば、一の位を四捨五入すると20になる整数を考えると、「17」は一の位を四捨五入すると20になりますし、「16」「21」もそうです。
このように四捨五入すると20になる整数は範囲に渡っていくつか存在します。その範囲を求めるのが「概数の復元問題」です。
「がい数の復元」のやり方を理解
まず、直接的に位を指定される方式です。
例題1-1
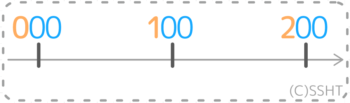
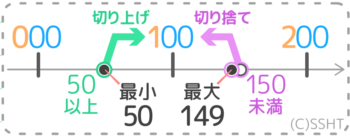
まず「一の位を四捨五入した」数直線上で、100の前後に来る数を考えます。
「一の位を四捨五入」ですから、一の位がゼロになった数が「０」「10」「20」「30」…100」と続きます。つまり今回の数直線上では、100の前後の数は「90」「110」になります(10刻みの数直線ということ)。
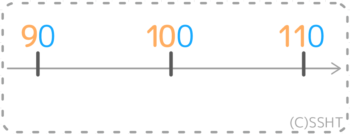
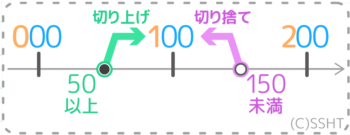
四捨五入で「100」になる数には、切り捨てで100になる数(A)と切り上げて100になる数(B)の二種類があります。
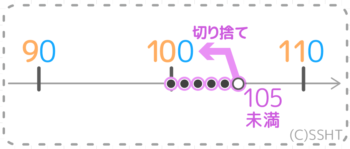
まず、切り捨てで「100」になる数の範囲を求めます。
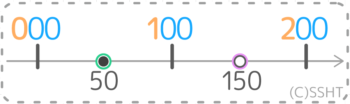
「100」の一つ後ろの目盛りは「110」で、概数と目盛りの真ん中は「105」になります。
そして四捨五入で切り下げになるのは真ん中よりも小さい範囲なので「100」以上「105」未満の整数(100,101,102,103,104)と分かります。
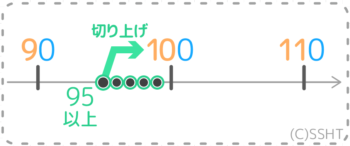
同様に、切り上げて「100」になる数の範囲を求めます。
概数「100」の一つ前の目盛りが「90」で概数との真ん中は「95」です。
四捨五入で切り上げになるのは真ん中以上なので、切り上げで「100」になるのは「95」以上で「100」未満の整数(95,96,97,98,99)ですね。
そして、2つを合わせたものが求める範囲で、最大最小も分かります。
範囲は95以上105未満になります。
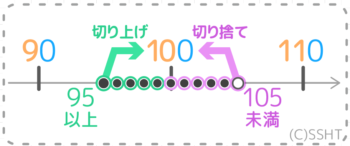
最小は95ですが、最大は105は入らない(未満)ので104が答えです。
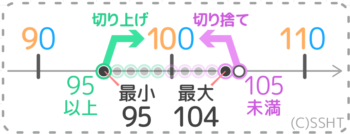
範囲:95以上105未満
最小95,最大104
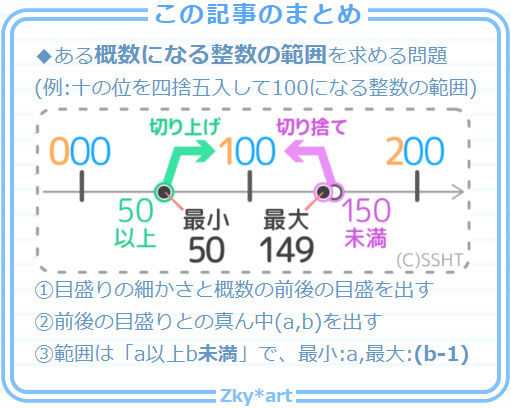
このように、概数から範囲を求める「復元問題」は３ステップで解いていきます。
- どの位がゼロになるか考えて概数の前後の数(A,B)を出す
- 概数とA,Bとの真ん中(a,b)を出す
- 「a以上b未満」が答えになります。
試しに、もう1問練習します。
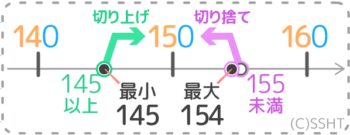
例題1-2
先程の３ステップでいきます。
ステップ❶どの位がゼロになるか考えて前後の数を出す
「十の位を四捨五入」なので、十の位と一の位が０の数が「000」「100」「200」「300」と続いていきます。概数100の前後の目盛りは0と200です(この問題の数直線は百刻みということです)。
ステップ❷概数とAの真ん中の数a,概数とBの真ん中の数bを出す。
概数100と目盛りの真ん中の数は「50(a)」と「150(b)」です
ステップ❸
「50」以上「150」未満ですね
これで最小と最大も分かりますね。
最大が150ではなく149なのに注意して下さい。
範囲:50以上150未満
最小50,最大149
爽茶練習問題で定着！
類題1-1
①ゼロになるのは一の位で、概数150の前後の数は140と160(この問題で数直線は十刻み)
②概数と目盛りの真ん中は「145」と「155」
③範囲は145以上155未満。最小は145最大は154
答:範囲 145以上155未満
最小145最大154
もう1問やってみましょう。
類題1-2
①ゼロになるのは十の位で、概数2200の前後の数は2100と2300(数直線は百刻み)。
②概数と前後の数の真ん中は2150と2250
③範囲は2150以上2250未満。最小が2150、最大が2249 ですね
答:範囲 2150以上2250未満
最小2150最大2249
爽茶以上で「直接指定される場合」の復元問題は終了です。
次は０にする位を直接は指定されない場合です。
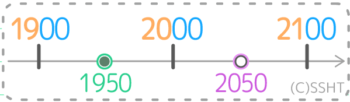
直接指定がない場合
爽茶これも先程と同じ3ステップで解けばOKです。
- 目盛りの細かさを読み取り、前後の目盛り(A,B)を出す
- 概数とA,Bの真ん中(a,b)を出す
- 範囲は「a以上b未満」
やり方を理解♪
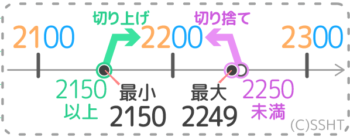
例題2
ステップ①
ステップ②
概数と前後の数の真ん中は「1950」と「2050」になります
ステップ③
これで答えが分かりますね
答:範囲 1950以上2050未満
最小1950最大2049
やり方はさっきと同じ3ステップで行けますね。類題で練習して下さい。
練習問題で定着!
類題2-1
❶上から1ケタの概数なので、上から2ケタ目とその下が0になりますから「0000」「1000」「2000」と数が並び、概数2000の前後の目盛りは「1000」と「3000」になります(数直線は千刻み！)
❷概数2000と前後の数の真ん中は「1500」と「2500」
❸範囲は、1500以上2500未満。最小が2499なのに注意しましょう。
答:範囲 1500以上2500未満
最小1500最大2499
類題2-2
❶百の位から0になるので千刻み(1000,2000…)で、34000の前後の数は33000と35000。
❷概数と前後の数の真ん中は33500と34500。
❸範囲は33500以上34500未満なので、最小の整数が33500,最大の整数が34499 です
答:最小33500,最大34499
類題2-3
❶上から3ケタ(千の位)から0になるので一万刻み(10000,20000)で、980000の前後の数は970000と990000。
❷概数と前後の数の真ん中は975000と985000。
❸範囲は975000以上985000未満なので、最小が975000,最大が984999
答:最小975000,最大984999
爽茶プリント
画像をクリックするとプリントが表示されますので保存して下さい。
メアド等の入力は必要ありませんが、著作権は放棄しておりません。無断転載引用はご遠慮ください。
爽茶概数の復元問題の解き方が分かりましたか？概数の応用問題は他にもあるので是非見て下さい。
●
歴史を学習する小学生の保護者の方へ
年表,年号,地図,書き取りテストなど400枚のプリントがセットになったそうちゃ式オリジナル教材が8/25(日)までお買い得価格！興味がある方はコチラへ
2023年度生徒さん募集
2023年度の生徒さんの募集を開始しました(対面授業の一次募集)
東武野田線・伊勢崎線沿線にお住まいの新5年生で予習シリーズをベースにされている方が対象です。
詳しくはコチラのページを御覧下さい
新4年生の方を対象に学習相談/授業を実施します(2次募集はサピックス新越谷校・南浦和校の方のみ対象。締め切り1/27)。応募はコチラから
中学受験でお悩みの方へ
爽茶「中学受験と高校受験とどちらがいいの？」「塾の選び方は？」「4年次・5年次はどう勉強すればよい？」「志望校の過去問が出来ない…」など
様々なお悩みへのアドバイスをまとめたので参考にして下さい。
もしかしたら、自分だけで悩んでいると煮詰まってしまい、事態が改善できないかもしれません。講師経験20年の「そうちゃ」に相談してみませんか？対面/オンラインの学習相談を受け付けているので、ご利用下さい。