(小4)切り上げと切り捨て
(小4)四捨五入
(小4)標準1(計算の見積もり)
(小4)四捨五入すると~になる数
(受験)わり算の答えからの復元
(受験)概数の和と差
(特)がい数の公式まとめ
「がい数が分からない・苦手・嫌い!」という小学生の方、安心して下さい!東大卒講師歴20年の図解講師「そうちゃ」が重要基本事項を分かりやすく解説します。この記事を読み終える頃にはがい数に対する苦手意識は吹っ飛んでいるでしょう♪
がい数は小4にとっては結構難しいです。しかもその後は概数を教わることは一切ありません…ですから良くわからないとか忘れたというのはよくある事ですね。
下の目次から好きなところをクリックして読んで下さい。
目次(クリックでジャンプ)
数の種類と範囲
数の種類
「~数」の意味とイメージを正確に覚えましょう
- 「整数」→1で割り切れる数
(-3,-2,-1,0,1,2,3など)数直線上の整数
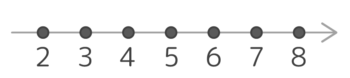
- 「自然数」→整数のうち、正(プラス)の数
(1,2,3など。0は自然数ではありません!) - 偶数と奇数
- 「偶数」→2の倍数。2で割り切れる数
(2,4,6,8,など) - 「奇数」→2で割り切れない数
(1,3,5,7,9など)数直線上の偶数(黒)と奇数(白)
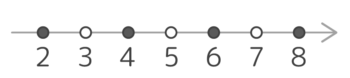
- 「偶数」→2の倍数。2で割り切れる数
- { 0 , 12, 1 , 0.3 }のうち整数は?
→( 0と1。0も整数です。 ) - { 9014 , 0.4 , 13 , 105 }のうち偶数は?
→( 偶数は「一の位が2か4か6か8か0の整数」なので、9014 )
数の範囲
範囲を表す言葉の意味とイメージを数直線と一緒に覚えます。
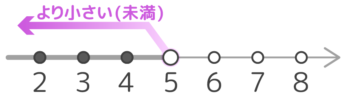
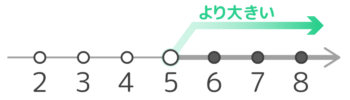
「より」大きい「より」小さい(未満)
区切りは範囲に含まれません。
例えば「5より大きい」は、4はもちろん、5もダメです。5よりちょっとでも大きければ(5.01や5.00…01など)OK。
また「5より小さい(5未満)」は6はもちろん、5もダメです。5よりちょっとでも小さければ(4.99や4.99…9等)OK。
数直線上に表す時は区切りを白い丸で表します。
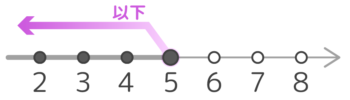
「以」上「以」下
こちらは区切りが範囲に含まれます。
例えば「5以上」だと4はダメですが、5はOK。
「5以下」だと6はダメですが、5はOKです。
数直線上に表す時は黒い丸を使います
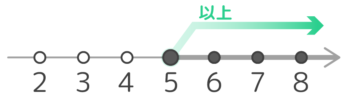
- 4以上8以下の整数はいくつあるか?
→( 4と5が含まれる。4,5,6,7,8 の5個 ) - 10より大きく15未満の整数はいくつあるか?
→( 10と15は含まれない。11,12,13,14の4個 ) - 4以上10未満の偶数はいくつあるか?
→( 4は含まれるが10は含まれない。4,6,8 の3個 ) - 21より大きく33以下の奇数はいくつあるか?
→( 21は含まれないが33は含まれる23,25,27,29,31,33 の6個 )
数の範囲の文章問題
モノの数量がピッタリと確定せずに幅をもって決まる場合に、その幅(範囲)を求める問題
例題
ある本を、毎日5ページずつ読むと10日目に何ページか読んで全部読み終わる。この本のページ数の範囲を求めなさい[予夏必3例2′]
9日目までに読んだページ数は5×9=45ページで、これはピッタリ確定します。
10日目に読んだページは「何ページか」とあるのでピッタリとは決まらず幅があります。
一番少ない場合が1ページ(0ページでは読んだことにならない)で、多い場合が5ページです。
したがって、本のページ数は最も少なくて45+1=46ページ、最も多くて45+5=50ページと分かります
46ページ以上50ページ以下
類題
沢山のアメを袋に小分けした。1袋に8個づつ詰めていくと25番目の袋に何個か詰めたところでアメが無くなった。アメの個数の範囲を求めなさい
最も少なくて(8×24)+1=192+1=193個
最も多くて(8×24)+8=192+8=200個
193個以上200個以下
概数とは?
概数の意味
言葉の意味としては「大まかな数」ですが、その反対の「きっちりした数」を考えると本当の意味が分かります。
概数でない数「きっちりした数」
「きっちりした数」はできるだけ正確に測った数です。
ただ、本当に正確に測ろうとすると無限に細かくなってしまいます(>_<)
(例)1.23456789… キリが無い!
概数(およその数)
上のように細かく測るとキリがないので、細かさに限度(目盛り)を決めたのが概数です。
例えば「1.23456789…」を一の位までしかない目盛り(1,2,3,4…)だけで測ると、1.23456789…は「1」と「2」の目盛りの間にあるので、思い切って「1」か「2」のどちらかにすれば済みますね。
この「1」や「2」が概数で、今の例では「1.23456789…」を一の位までの概数にしたことになります。
がい数の決め方
上の例では1.23456789を「1」と「2」どちらにするかという基準が必要になります。
基準が三通りあります。
●切り捨て→とにかく小さめ(1)にする
●切り上げ→とにかく大きめ(2)にする
●四捨五入→端数(この場合は小数点以下の部分)によって「切り捨て」か「切り上げ」のどちらかにする
小まとめ
●がい数の意味
=細かさに限度(目盛り)をつけて測った数
(例)1.23456…
→目盛りを一の位までにして測ると「1」か「2」
この「1」や「2」が概数
●がい数の決め方
├①切り捨て(とにかく小さくする)
(例)「1.23456…」を一の位までで切り捨て→「1」
├②切り上げ(とにかく大きくする)
(例)「1.23456…」を一の位までで切り上げ→「2」
└➂四捨五入(半端な数次第で決める)
(例)「1.23456…」を一の位までで四捨五入
→「0.23…」で「2」より「1」に近い
→「1」にする
切り捨てと切り上げ
まず切り捨てた数を出し、それを元に切り上げた数を出します。
切り捨てのやり方
切り捨ての方法は三種類あります。
A「~の位を切り捨て(上げ)なさい」
→その位からゼロにする
B「~の位までの概数にしなさい」
→一つ下の位からゼロにする
C「上から~ケタの概数にしなさい」
→上から+1ケタからゼロにする
A:~の位を切り捨て
「~の位を切り捨てなさい」と言われた場合は、指定された位(から右)をゼロにします。
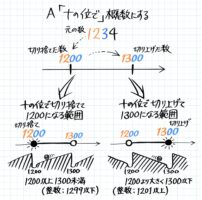
(例)「1234を百の位で切り捨てなさい」と言われたら、百の位から(右を)ゼロにするので1000が切り捨てた数です。
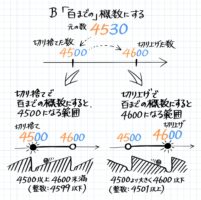
B:~の位までの概数
「~の位『までの』概数にしなさい」と言われた場合は、そのひとつ下の位から右をゼロにします。
例えば「1234を百の位までの概数にする」場合、百のひとつ下の十の位からゼロにするので1200が切り捨てた数です。
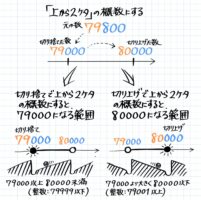
C:上から~ケタの概数
「『上から』~ケタの概数にしなさい」と言われた場合は、上から+1ケタ目から右をゼロにします。
例えば「12345を上から2ケタの概数にする」場合、2に+1して上から3ケタ目からゼロにするので12000が切り捨てた数です。
切り上げのやり方
切り上げは、問題の聞かれ方に関わらずいつも同じ方法です。切り捨てた数のゼロにした部分より左の部分(目盛り)を+1します。
(例)
切り捨てた数が230→切り上げると240
切り捨てた数が12300→切り上げると12400
切り捨てた数が99000→切り上げると100000
全体を通してみると、切り捨てがAタイプの場合、こうなります。
- まず、指定された位をゼロにして切り捨てた数を出します。

- 次に、ゼロにした位より左を+1して、切り上げた数を出します

テストで確認しましょう。切り捨てにはABC三種類ありますが、切り上げはどれも同じです。
以下の指示に従って「3572」を概数にしなさい。
(1)一の位で切り捨てなさい
→( 一 )の位からゼロにする→( 3572→3570 )
(2)十の位で切り上げなさい
→切り捨てると(3572→3500)
→切り上げると( 切り捨てた数3500→3600 )
(2)百の位で切り上げなさい
→切り捨てると(3572 → 3000)
→切り上げると( 切り捨てた数3000→4000 )
以下の指示に従って「3572」を概数にしなさい
切り捨てて十の位までの概数にする
→( 1つ下の一 )の位をゼロにする→( 3572→3570 )
(2)切り上げて百の位までの概数にする
→切り捨てると( 1つ下の十の位からゼロにして、3572→3500)
→切り上げると( 切り捨てた数3500→3600 )
(3)切り上げて千の位までの概数にする
→切り捨てると( 1つ下の百の位からゼロにして、3572→3000)
→切り上げると( 切り捨てた数3000→4000 )
以下の指示に従って「3572」を概数にしなさい
(1)切り捨てて上から2ケタまでの概数にする
→上から( 3 )ケタ目からゼロにする→( 3572→3500 )
(2)切り上げて上から3ケタまでの概数にする
→切り捨てると( +1した上から4ケタ目からゼロにして、3572→3570)
→切り上げると( 切り捨てた数3570→3580 )
(3)切り上げて上から1ケタまでの概数にする
→切り捨てると( +1した上から2ケタ目からゼロにして、3572→3000)
→切り上げると( 切り捨てた数3000→4000 )
もう少し詳しい説明を読みたい人は「切り捨てと切り上げ」を見て下さい
四捨五入
まず上のやり方で切り捨てた数と切り上げた数を出し、次にその真中の数を出します。もとの数が真ん中の数より小さければ切り捨て、それ以上なら切り上げをします。
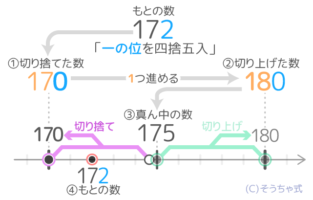
切り捨てゾーンと切り上げゾーンを決める。
172は切り捨てゾーンにある。
全体を通してみると、切り捨てがAタイプの場合、こうなります。
- まず、指定された位をゼロにして切り捨てた数を出します。

- 次に、ゼロにした位より左を+1して、切り上げた数を出します

- 切り捨てた数(X)と切り上げた数(Y)の真ん中の数(Z)を出します。
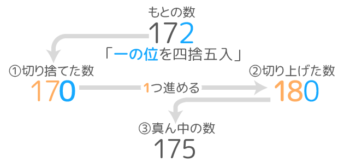
- もとの数が真ん中の数より小さければ切り捨て、以上なら切り上げます。

ここでは切り捨てて170が答えになります
詳しい説明は「四捨五入」を見て下さい
小数と概数
やり方は変わりませんが、答える時に右端の「0」を書いてはいけないのが注意点です。
概数の利用
計算結果の予想(見積もり)に概数を使えます。
例えば、2020×195の答えは2020が2000、195が200に近いので、掛け算の答えは2000×200=400000に近くなるだろうと予測できます。実際の答えは393900。400000に近いですよね?
また円周率を使った3.14×22の答えも、3.14は3に近く、22は20に近いので、3×20=60に近くなるだろうな…と予想できます。実際の答えは69.08。これも近いです♪
このように予想してから落ち着いて筆算をすれば計算ミスをしても気づくことが出来ます。
概数の復元
ある概数から、もとの数の範囲を復元します。
復元の方法
切り上げ・切り捨てからの復元
3タイプそれぞれを図にすると、こんな感じでしょうか
四捨五入からの復元
詳しい説明は「四捨五入すると~になる数」を見て下さい。
乗除からの復元(応用:中学受験)
●わり算の答えが概数として示される数
の範囲と最小・最大を求める問題
(例)9で割った答えを小数第一位で四捨五入すると
7になる数Nの最小最大を求める
→割った答えの範囲を求めて(6.5以上7.5未満)
範囲の下限と上限を倍する(58.5以上67.5未満)
倍した範囲内の最大最小の整数(59,67)が答え
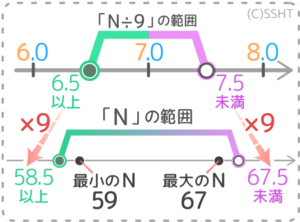
詳しい説明は「割り算の答えからの概数の復元」を見て下さい。
概数の操作
概数の和と差
がい数=範囲がある数同士を足したり引いたりすると答えにも範囲が生まれてしまいます。
例えば7以上10以下のAと2以上5以下のBを足した場合、小さい方同士を足した2+7=9が最小、大きい方同士を足した5+10=15が最大で、A+Bは9以上15未満になります。
また引いた場合は小さいBの最大と大きいAの最小の差7-5=2が差の最小、Bの最小とAの最大の差10-2=8が差の最大になり、A-Bは2以上8以下になります。
詳しい説明は「概数の和と差」を見て下さい。
概数のまとめは以上です。
オリジナル教材のご案内
御三家・早慶付属など難関・人気の中学に合格した2025年度の受験生達から大好評!
分かりやすいのはもちろん、スキマ時間にお子様一人で反復定着できますよ
人気教材はこちら(クリックするとショップ内教材ページにジャンプ)
●歴史 ●時事問題(2025年) ●世界地図 ●世界遺産
■仕事ニュートン算 ■食塩水 ■売買損益
★月の形 ★電流 ★水溶液/気体の性質
その他にも社会/理科/算数の教材がございます。興味がある方は公式ストアへどうぞ