「倍数・公倍数を予習したい」という小学4年生の方、「復習したい」という小学5年生の方、お任せ下さい♪
東大卒講師歴20年の図解講師「そうちゃ」が分かりやすくまとめました。
この記事を理解すれば倍数・公倍数の基本は身につきますよ！
目次(クリックでジャンプ)
倍数
倍数の意味
こんにちは！「そうちゃ」@zky_tutor(プロフィール)です。
実は、小学5年生の人は倍数をもう習っています！3年前に習って、算数の授業の時は毎回使っています！
もう少し正確に言うと、倍数は小2で習った○○の延長です。〇〇は何でしょうか？
1:倍数の意味
「ある数Aを□した数をAの倍数と言う。従って、Aの倍数をAで割ると必ず□できる」
ヒント
はじめなので気楽に答えて下さい
解説
ある数Aを1倍,2倍,3倍,4倍…した数をAの倍数と言う。
従って、Aの倍数をAで割ると必ず割り切れる。
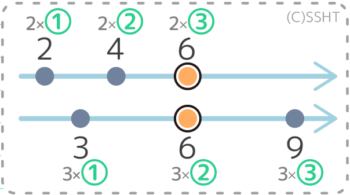
例えば、３の倍数は、3を1倍した「３」,2倍した「6」,3倍した「9」,4倍した「12」…というように続いていきます。
この 3,6,9,12…という数字の列を見たことありませんか？
そうです。掛け算(九九)の3の段ですね。
つまり倍数は九九の延長です。
◇九九
3,6,9,12,15,18,21,24,27(終了)
◆倍数
3,6,9,12,15,18,21,24,27,30,33…(ずっと続く)
九九では9の段までしかありませんが倍数は10の段よりも大きい数も扱います。(何でもインドでは20までを九九で暗記するらしいですけど(汗))
また、「～で割り切れる」というのも倍数の特徴です。この表現も覚えておきましょう。
まとめると、「倍数」はこんな数です。
「BがAの倍数」であるとき
→①BはAを2倍・3倍したもの
→②BはAで割り切れる
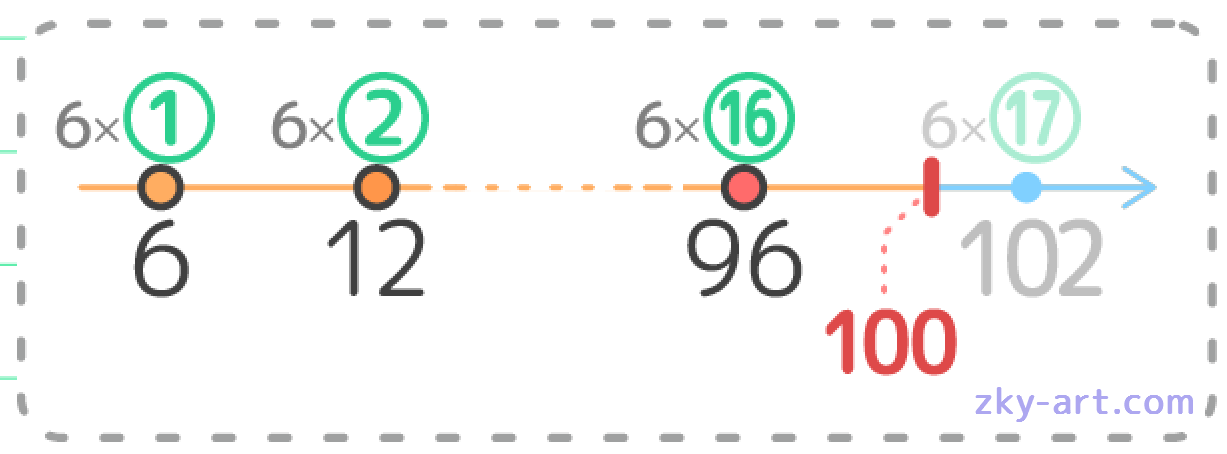
(例)Aが7の倍数
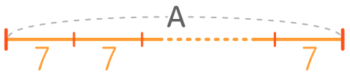
❶Aは7の2倍・3倍…と永遠に増えていく
❷Aは７で割り切れる
倍数の意味が分かったので、それを使った問題にチャレンジです！
( ･`ω･´)
1-1:倍数の問題
ヒント
「で割り切れる数」と言えば…
解説
「7で割り切れる数」＝「７の倍数」なので、九九の7の段の5番目までを数えます。
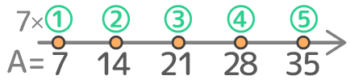
目盛りの無い数直線(右向きに矢印をつけます)を書き、その上に7×①から等間隔に５つ並べてると…
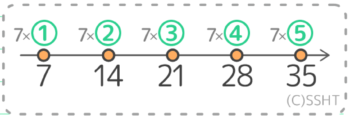
このようになります。7×①=7,7×②=14,7×③=21,7×④=28,7×⑤=35,の5つが答えです。
もう一問どうぞ
1-2:倍数の問題
解説
類題1と同じ様に、13×①から13×⑤を書くと
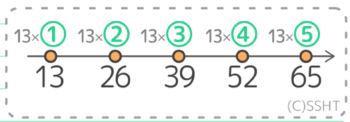
こうなるので、答えは13,26,39,52,65です。
偶数と奇数
2の倍数は特別！
色んな数の倍数の中でも、2の倍数は特別に「偶数」という呼び名があります。
そして2の倍数でない数は「奇数」と呼びます。
数を1,2,3と数えていくと…
1(奇数),2(偶数),3(奇数),4(偶数)…99(奇数),100(偶数),101(奇数)…999(奇数),1000(偶数),1001(奇数)…というふうに、偶数と奇数が交互に現れます。
つまり、全ての数は「偶数」か「奇数」に分けられます。
偶数奇数の見分け方
偶数・奇数の見分け方は簡単です。どんなに大きな数でも一の位が「2」「4」「6」「8」「0」なら偶数、「1」「3」「5」「7」「9」なら奇数です。
確認テストをどうぞ
偶数か奇数か判定しなさい
119→( 一の位が9なので奇数 )
80008→( 一の位が８なので偶数 )
3000000→( 一の位が0なので偶数 )
小まとめ
◆偶数…2の倍数である数
◇奇数… 〃 でない数
●見分け方
→ 一の位が2,4,6,8,0のどれかなら偶数
(例)「1236」→偶数
「1237」→奇数
学校教科書の「倍数」の問題は以上です。
もっと問題を解きたい人は、記事下のオススメ問題集を見て下さい。
また、中学受験用のより高度な内容を学びたい人は姉妹サイト「そうちゃ式算数 新1号館」の「(公)約数倍数」を見て下さい。
プリントダウンロート
(準備中)
無断転載引用はご遠慮ください。
公倍数
公倍数の意味
「公倍数」の「公」は「共通する」という意味なので、公倍数は2つ以上の数に共通する倍数ということになります。
そこで、上で見た「倍数」の意味を元に公倍数の意味を考えると、こうなります。
「XがAの倍数」であるとき
①XはAを2倍・3倍したもの
②XはAで割り切れる
「XがAとBの公倍数」であるとき
①XはAを何倍かした数で
Bを何倍かした数でもある
②XはAでもBでも割り切れる
例えば、18という数は、6を3倍、9を2倍した数になっています。つまり18は6と9の公倍数です。そして、18は6でも9でも割り切れますね！
クイズ感覚の問題で確認してみましょう。
2:公倍数の識別
ヒント
「割れるか」どうか考えればOKです
解説
45は9でも5でも割れるので、9と5の公倍数です。
解説
42は7で割り切れますが8では割り切れないので、7と8の公倍数ではありません。
解説
48は6でも8でも割れるので、6と8の公倍数です。
公倍数の意味は分かりましたね？
次は公倍数を「求める」練習をしてみます。
公倍数の求め方(書き出し法)
ここでは、紙に書いて(イメージして)求める方法(書き出し法)を練習します。
2:公倍数を求める(1)
解説
２の倍数は２を1倍、2倍…と倍していった数ですから、小さい方から書くと、 2 , 4 , 6 …となります。
3の倍数も同じように考えて 3 , 6 , 9 … と続きます。
さて、同じ数(共通するもの)が出てきましたが、なんでしょうか？
「６」ですね！
この６は一番最初で一番小さい公倍数なので最小公倍数と言います。
2:公倍数を求める(2)
次に、その上に2の倍数を小さい方から一つづつ書き、3の倍数と共通するものを見つけなさい
ヒント
面倒臭がらずに書いて下さい
(^_^;)
解説
2つの数の公倍数を書き出しで求める場合、大きい方を先に書くのがラクチンです。今回は2と3なので、3の倍数を書きます。まず３の倍数を 3,6,9,12,15,18 と書き、その上に２の倍数を書いていき、3の倍数と同じものが出たら公倍数です。
2,4,6! はい出ました。最初の公倍数6です
さらに続けて 8,10,12! 2つ目の公倍数は12です。
さらに続けて 14,16,18! 3つ目の公倍数は18です。答: 6,12,18
さて、今の答えを見て何か気づきませんか？
そうです！
２と３の公倍数は６の倍数になっています。このあと 6,12,18,24,30…と続いていきます。
そして、６は2と3の最小公倍数でしたか。
したがって公倍数は最小公倍数の倍数になります。
公倍数は最小公倍数の倍数
(例)2と3の公倍数
2と3の最小公倍数「6」の倍数になる
この性質を使うと、公倍数の問題を簡単に解けるので、試してみましょう。
2:公倍数を求める(3)
ヒント
「公」倍数ではなく、ただの「倍数」にして解いて下さい
解説
「2と3の公倍数」は「最小公倍数６の倍数」なので、
この問題は、「６の倍数の10番目は何か？」と同じです。
60倍数の10番目なので、6×⑩=60になりますね。
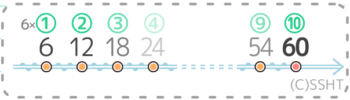
このように公倍数の問題は、ただの倍数の問題に直すと簡単に解くことができます
以上が公倍数の基本になります。まとめると…
●公倍数
＝2つ以上の数に共通する倍数
＝2つ以上の数で割り切れる数
●最小公倍数＝はじめの(一番小さい)公倍数
●公倍数は最小公倍数の倍数
この性質を使って問題を解いてみましょう。
2-1:公倍数の問題
解説
3と５の最小公倍数は15なので、3と5の公倍数は15の倍数と同じです。
そして15の倍数の20番目は、15×20＝300 と分かります
ここまでの問題では、2と3の最小公倍数→6、3と5の最小公倍数→15 という風に、最小公倍数は2つの数のかけ算になっていたのに気づいた人もいると思います。
ただ、必ずそうなるとは限りません。素数同士だとそうなります。素数を知りたい人は「素数と素因数分解」を見て下さい。
2-1:公倍数の問題
解説
6の倍数を、書き出していき、4の倍数でもある数が出てきたら、それが最小公倍数です。
6 , 12 はい来ました！早かったですねｗ
これで、この問題は12の倍数の30番目を出す問題と同じなので、12×㉚=360と分かります。
今度は逆から聞く問題です。
2-1:公倍数の問題
ヒント
まずは、10と14の最小公倍数を求めましょう
解説
14の倍数を書き出して10の倍数でもある数(1の位がゼロ)が出てくれば最小公倍数です。
14 , 28 , 42 , 56 , 70 はい来ました！
これで「10と14の公倍数」は「70の倍数」と同じ意味ですから、この問題は「210は70の倍数としては何番目か」と同じですね。
70を何倍すれば210になるか？ということなので、10÷70=3 から3番目と分かります。
公倍数の問題は以上です。お疲れさまでした
もっと問題を解きたい人は下にあるオススメ教材を見て下さい。
また、より高度な中学受験用の内容を学びたい人は姉妹サイト「そうちゃ式算数 新1号館」の「(公)約数倍数」を見て下さい。
小まとめ
●公倍数＝2つ以上の数に共通する倍数
●最小公倍数
＝最初の公倍数。公倍数は最小公倍数の倍数になる
● 公倍数の求め方(書き出し法)
_(例：2と3の公倍数の求め方)
❶大きな方(3)の倍数を書き出していき、小さな方(2)の
＿倍数にもなっている最初の数(最小公倍数=6)を見つける
❷最小公倍数(6)の倍数を書いていく
プリントダウンロード
(準備中)
無断転載引用はご遠慮ください。
倍数・公倍数が分かりましたか？公約数公倍数の総合案内から他の記事も読んで下さい。
おすすめ教材
爽茶オススメ問題集
●「毎日のドリル」(学研)はスマホアプリとの連携でやる気をアップできる問題集です。(くわしい案内はこちら)。
●約数/公約数だけを応用問題まで特訓したい人には「倍数・公倍数」(サイパー算数)がオススメ
「分かりやすい！」と評判の
今なら14日間無料♪この期間内に利用を停止すれば料金は一切かかりません。この機会に試してみては？
歴史を学習する小学生の保護者の方へ
年表,年号,地図,書き取りテストなど400枚のプリントがセットになったそうちゃ式オリジナル教材が8/25(日)までお買い得価格！興味がある方はコチラへ
2023年度生徒さん募集
2023年度の生徒さんの募集を開始しました(対面授業の一次募集)
東武野田線・伊勢崎線沿線にお住まいの新5年生で予習シリーズをベースにされている方が対象です。
詳しくはコチラのページを御覧下さい
新4年生の方を対象に学習相談/授業を実施します(2次募集はサピックス新越谷校・南浦和校の方のみ対象。締め切り1/27)。応募はコチラから
中学受験でお悩みの方へ
爽茶「中学受験と高校受験とどちらがいいの？」「塾の選び方は？」「4年次・5年次はどう勉強すればよい？」「志望校の過去問が出来ない…」など
様々なお悩みへのアドバイスをまとめたので参考にして下さい。
もしかしたら、自分だけで悩んでいると煮詰まってしまい、事態が改善できないかもしれません。講師経験20年の「そうちゃ」に相談してみませんか？対面/オンラインの学習相談を受け付けているので、ご利用下さい。