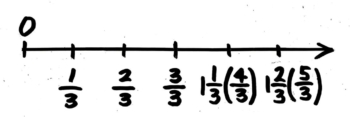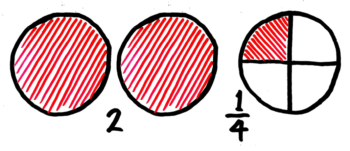「分数ってどんな種類あったけ?」「仮分数と帯分数の直し方を忘れた」という小学4年生の方へ
分数の種類については「帯分数」「仮分数」をお互いに変形できるようになればオシマイです。つまり2つの方法を覚えるだけです。やる気が出てきませんか?
この記事では、東大卒講師歴20年の図解講師「そうちゃ」が「帯分数→仮分数」「仮分数→帯分数」のやり方を分かりやすく説明します。
記事を読んで真似すれば、分数を好きな形に自由自在に変形できるようになりますよ!
目次(クリックでジャンプ)
分数の種類
 爽茶
爽茶こんにちは!「そうちゃ」@zky_tutor(プロフィール)です。
はじめに分数の3つの種類を見ていきましょう♪
三つの種類(形)
分数には三種類の形があります。
(1)真分数(しんぶんすう)
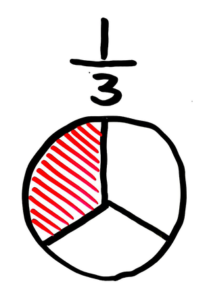
分母(下)が分子(上)より大きい形を真分数と言います。
13←分子が小さい←分母が大きい
今まで習っていたのはこの形です。図にすると、こうなります。
1個のパンを分ける図になります
ここからの2つが、新しく習う形です。
(2)帯分数(たいぶんすう)
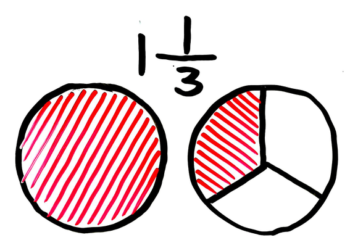
真分数の左に数(整数)がついて整数と分数を足した形を「帯分数」と言います。
図にするとこうなります。
整数部分は分けていないパン丸ごと1個になります
(3)仮分数(かぶんすう)
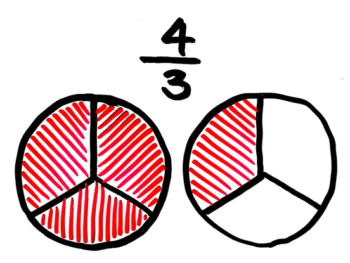
分子(上)が分母(下)より大きい形は「仮分数」と言います。
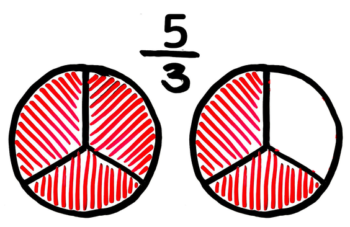
図にするとこうなります
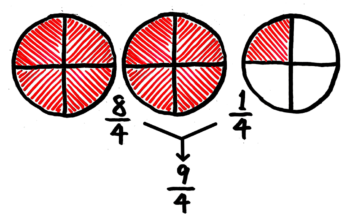
2つ以上のパンを分ける図になります。この図を見て何か気づきませんか?
そうですね。さっき見た真分数の113と同じ量を表していますね。
つまり43は113と書き換えることが出来ます。(後で練習します!)
形を見分ける練習
それでは、この3つの形を見分ける練習をしてみましょう。
例題1(分数を見分ける)
(1)114 (2)1115 (3)139 (4)77
分数の3つの形「真分数」「帯分数」「仮分数」が理解できましたね?
●ちょっと応用
「算数が得意だ」興味がある」という人向けです。
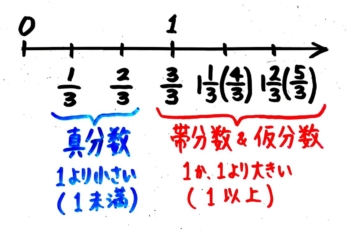
43と113で見たように帯分数と仮分数の中身は同じなので、分数は「真分数」と「仮分数&帯分数」の2グループに分けることができます。
この2グループの違いというか、境界線、分かれ目は何だと思いますか?
もっと問題を解きたい人は下にある「オススメ教材」を見て下さい
仮分数を
帯分数へ直す
 爽茶
爽茶さっきチラッと書きましたが、帯分数と仮分数は同じものです。
仮分数を帯分数に直す方法
まず、仮分数を帯分数に直す方法を練習してみましょう。
●例題2-(1)
●例題2-(2)
直し方を公式にする
例題のように図を書いて求めても良いですが、もっとパッと直せるように公式(数字の計算の形にしたものを「公式」と言います)にしてみましょう♪
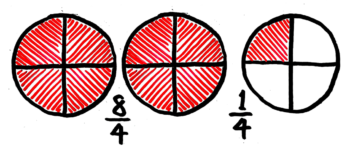
もう一回、直す前と後を並べるとこうなります。
直す前と後で、分母は3で変わりません。
では、帯分数の横の数字1と分子2 この2個の数字はどうやって出てきたのでしょう?
さっきの図で「三等分5ピースから3ピースをまとめて丸ごと1個が出来て、2ピースは余る」と考えたからです。
これは余りのあるわり算「5÷3=1余り2」をしていたのと同じです。
公式を使う練習
では、この公式を使ってサッ!と計算で仮分数を帯分数に直す練習をしてみましょう。
類題2(仮分数→帯分数)
(1)73 (2)112 (3)257 (4)474
公式通り余りのある割り算「仮分数の分子÷分母」をします
●類題2-(1)
●類題2-(2)
●類題2-(3)
●類題2-(4)
次は、帯分数を仮分数に直します。
帯分数から
仮分数に直す方法
 爽茶
爽茶今度は反対方向「帯分数→仮分数」の直し方です。
直し方を考える
例題3(帯分数→仮分数)
●例題3-(1)
●例題3-(2)
直し方を公式にする
こちらは分かりやすいですね。
今の計算「(2×4)+1=9」がそのまま仮分数の分子になりました。
そして、分母は変わらないので、214→(2×4)+14→94になるのですね
帯分数ACBは仮分数(A×B)+CBに直せる。
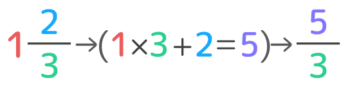
公式を使う練習
では、類題で練習をしてみましょう
類題3(仮分数に直す練習)
公式の通りに「(横の整数×分母)+分子」 を計算しましょう
●類題3-(1)
●類題3-(2)
●類題3-(3)
●類題3-(4)
これで「分数の種類と直し方」は終了です!
もっと問題を解きたい人は記事の下の「オススメ教材」を見て下さい
記事のまとめ
最後に記事のまとめです。
●3つの種類がある
(真分数) (帯分数) (仮分数)
23 123 53
●異なる種類に直す
○仮分数を帯分数に直す(分母÷分子)
○帯分数を仮分数に直す(整数×分母+分子)
これで三種類の分数を自由に使えるようになりましたね!
他にも分数の記事があるので「分数の総合案内」から見て下さい!
おすすめ教材
 爽茶
爽茶オススメ問題集
●「毎日のドリル」(学研)はスマホアプリとの連携でやる気をアップできる問題集です。(くわしい案内はこちら)。
●「分数の計算(算数基礎マスター)」は3年から6年の分数計算をカバーしているので学校の予習復習はもちろん、中学受験に向けた先取り学習にも使えます。低学年のうちに買うと長く使えてオトクですよ!
「分かりやすい!」と評判の
今なら14日間無料♪この期間内に利用を停止すれば料金は一切かかりません。この機会に試してみては?
オリジナル教材のご案内
御三家・早慶付属など難関・人気の中学に合格した2025年度の受験生達から大好評!
分かりやすいのはもちろん、スキマ時間にお子様一人で反復定着できますよ
人気教材はこちら(クリックするとショップ内教材ページにジャンプ)
●歴史 ●時事問題(2025年) ●世界地図 ●世界遺産
■仕事ニュートン算 ■食塩水 ■売買損益
★月の形 ★電流 ★水溶液/気体の性質
その他にも社会/理科/算数の教材がございます。興味がある方は公式ストアへどうぞ