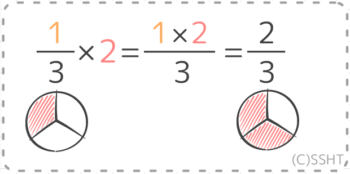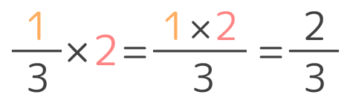爽茶
爽茶こんにちは!「そうちゃ」@zky_tutor(プロフィール)です。
小学5年生の最後に習うのが「分数と整数のかけ算・割り算」です。実は「足し算・引き算」よりも「かけ算・割り算」の方が簡単なので、安心して下さい!
目次をクリックすると好きな場所に飛べますよ。
目次(クリックでジャンプ)
分数×整数の計算方法
計算方法を理解
例題1(分数と整数のかけ算)
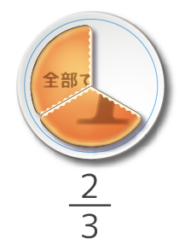
13はパンを三等分したうちの1ピースです(図1)。そして、13×2 は今の1ピースを2倍します(図2)。
つまり、13×2=23 だと分かります。23
さて…今の計算式をもう一度見るとこうなっています。
分母は変わらず、分子が2 になったということは…
これで、分数に整数を掛ける場合分子×整数をすれば良いということが分かりました♪
解かせ方・教え方の注意
(苦手意識を減らす)
分数は「苦手」「嫌い」という生徒が非常に多いので、分数を教えるときは「簡単だよ!」「これだけだよ!」と声掛けをしながら、実際にも簡明なやり方を教える必要があります。
ただ、通分がない分、足し算・引き算に比べるとかけ算・わり算は簡単なので、ここで分数に対する苦手意識を少しでも減らしてあげましょう。
手順(いきなり計算させない)
❶準備
問題文を確認したら、等号に続けて横線(括線)を長く書き(図1)、問題文の数字を長い横線の上下に「移します」(図2)。横に並んだ数字の間に「小さく」×記号を入れます(図3)。ここでは計算をせずに移すことに集中させます。
1 × 23
1 × 23 × 2
1 × 23 × 2
❷かけ算
準備が出来たら深呼吸でもして落ち着いて、それからかけ算を行います。
はじめはゆっくりこの手順をしっかり守らせながら、生徒に「なんだ、分数のかけ算は難しくないな(ホッ)」という事を実感させるのが大切です。
それでは、公式を使う練習をしてみましょう!
練習問題で定着
公式通りに計算すれば大丈夫ですよ!
●類題1(1)
分子と整数をかけ算します。
27×3=2×37=67です。67
●類題1(2)
悩まずに答えをだしてください。
整数が前にあっても、やり方は同じで、分子と整数をかけ算します。
2×311=2×311=611です。611
●類題1(3)
答え方に気をつけましょう
35×7=3×75=215 ですが…まだ答えではありません。仮分数は帯分数に直して答えます。
帯分数に直すには、余りのあるわり算で「分子÷分母」を行い、答えが帯分数の整数部分、余りが分子、分母は変わらず、でした。復習したい人は参考記事「分数のまとめ」内「分数の種類」を見直して下さい。
215 →(分子21÷分母5=4余り1)→415です。415
●類題1(4)
◯分数を◯分数に直して計算
帯分数は仮分数に直してかけ算をします。
帯分数を仮分数に直すには「(帯分数の整数部分×分母)+分子」で仮分数の分子を出し分母は変わりませんでした。参考記事「分数のまとめ」内「分数の種類」を見直して下さい。
214→(2×4+1=9:帯分数の分子)→94 と直すので、214×3=94×3=9×34=274 となります。
これをさらに帯分数に直します(はじめは面倒くさいですが、そのうち慣れますよ!)
274→(27÷4=6余り3)→634 です。634
もう一度、分数のかけ算のルールをまとめるとこうなります。
この後は、分数×整数の工夫をお教えします。
分数×整数の工夫
途中で○○が出来ます♪
「分数×整数」の計算方法が分かったついでに、もう一問やってみましょう。
例題2(かけ算の工夫)
215×3=2×315=615 ですが…終わりではありません。
約分ができますね。約分を忘れた人は参照記事「分数のまとめ」内の「約分」を見直して下さい。
615→(分母分子を3で割って)→25ですね。25
今、最後に約分をしましたが、実はもっと簡単なやり方があります。分子と整数をかける前のココ
ここで「2×3」のかけ算をせずに、分子の3と分母の15を約分して1と5にしてしまいます。
約分は斜め上と斜め下でも出来るんですよ!
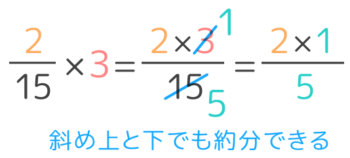
これに続けて 2×15=25 で終了です。
かけ算してから約分(わり算)するのよりもずっとラクチンですね。(このサイトでも、このように解いていきます。)
分子と整数をかける途中で約分をしても良い。
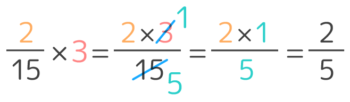
3ステップで作業させる
「わーっ」と解きたがる生徒を抑えて、「準備→約分→かけ算」という3ステップで解かせます。
❶準備
等号に続けて長い横線を書いて、そこに問題文の数値を「移す」。計算したり頭を使わせないのが大切。職人さんになったつもりでw丁寧に作業をさせる
❷約分
上と下の数字が約分できないか考え実行させる
❸かけ算
約分が終わったら初めてかけ算をする。
正しい手順で出来るようになったら、後は生徒それぞれの好みとペースに任せますが、結果が不正解の生徒には「『今日は』ゆっくり3ステップで解きなさい」と指示した方が良いですね。
それでは「途中で約分」をする練習をしてみましょう
工夫する練習問題
さっきのルール通りに計算しましょう♪
途中で約分をしても良い。
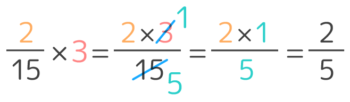
●類題2(1)
ウラワザを使いましょう
314×4=3×414→(分母14と分子4を2で約分)→3×27=67 です。67
●類題2(2)
 爽茶
爽茶「分数の総合案内」から「分数と整数のわり算」などを見ることができますよ。