「切り捨てとか切り上げがよく分からない…」という小学4年生の方、大丈夫ですよ！東大卒講師歴20年の図解講師「そうちゃ」が分かりやすく教えます。記事を真似すれば簡単にできるようになりますよ♪
目次(クリックでジャンプ)
切り捨て切り上げ
(Aタイプ:直接指定)
爽茶こんにちは！「そうちゃ」@zky_tutor(プロフィール)です。
切り捨て・切り上げの問題には３タイプあります。それぞれでやり方が少し違います。A「～の位を切り捨て(上げ)なさい」
B「～の位までの概数にしなさい」
C「上から～ケタの概数にしなさい」
まずAタイプから見ていきます。
切り捨て
Aタイプ「～の位を切り捨てなさい(～の位以下を切り捨てなさい)」のように位を直接指定される場合は一番簡単！指定された位とその下をゼロにするだけです。
1-1-1:Aタイプの切り捨て
解説
「一の位」と指定されているので一の位をゼロにします
172の場合、170になります。
解説
「十の位」と指定されているので十の位とその下をゼロにします3647の場合、3600になります。
簡単ですね！次はAタイプの切り上げです。
切り上げ
Aタイプ(位を直接指定される)切り上げの問題は、まず切り捨てた数を出して、それを利用します。
1-2-1:Aタイプの切り上げ
解説
まず「172を一の位で切り捨てた数」を考えると、一の位を0にした「170」でしたね。
ここで、切り捨てた数のゼロにしなかった部分に注目します。「170」の「17」の部分です。この部分を+1すると切り上げた数が出ます。
「17」の部分に+1するので「180」になります。これが172を一の位で切り上げた数です。
解説
まず「3647を十の位で切り捨てた数」を考えると、十の位から下を0にした「3600」でしたね。次に「切り捨てた数」のゼロにしなかった部分を+1します。「3600」の「36」の部分を+1するので「3700」になります。これが3600を十の位で切り上げた数です。
小数の位を指定
小数の位を指定された場合も同様です
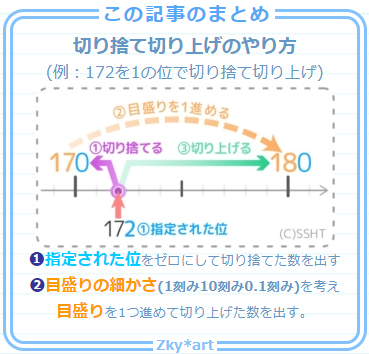
今のやり方をまとめると、こうなります。
(Aタイプ:位を直接指定)
(例)3647を十の位で切り捨て/切り上げ
- 指定された位(とその下)を0にして
「切り捨てた数」を出す3647→ 3600
- 切り捨てた数の0にしなかった部分を
+1して「切り上げた数」を出す。3647→ 3600→ 3700
切り捨てた数を聞かれていない場合でも、必ず切り捨てた数を求めることから始めましょう。
→このような数論の基本問題は、数学が苦手な生徒さんにとっては重要な得点源なので、緊張感あふれる摸試入試の場でも安心して確実に実行できるやり方を身に着けておくのが大事です。
試しに問題を解いてみましょう。
練習問題で定着！
1-2-1:
ヒント
❶切り捨てた数→❷切り上げた数 の順で出しましょう。
解説
❶切り捨てた数を出します。
百の位から下を0にするので「59000」です。
❷切り上げた数を出します。
0にしなかった部分「59」を+1して「60000」です。
さて、整数だけでなく、小数の位が指定される場合もあります。
1-2-2:
ヒント
答えを書くときに注意して下さい。
解説
❶切り捨てた数を出します。
小数第二位を0にするので「1.70」です。
❷切り上げた数を出します。
0にしなかった部分の小数点を抜かして「17」のつもりで+1して「1.80」になります。
また、答える時は最後の0をとって「1.8」と答えます。
爽茶切り捨て切り上げ(Bタイプ)
爽茶「～の位までの概数にしろ」という問題です。切り捨ての時に0にする位に注意します。
切り捨て
「～の位までの概数にしなさい」は指定された位の1つ下(右)からゼロにします。
例題で確かめましょう
2-1-1:
解説
「百の位まで」と指定されているので1つ下の十の位からゼロにします。
172の場合、100になります。
2-1-2:
解説
「十の位までの」と指定されているの一つ下の一の位をゼロにします。
3647の場合、3640になります。
「1つ下」に気をつければ簡単ですね！
切り上げ
切り上げのやり方はAタイプと全く同じで、切り捨てた数のゼロにしなかった部分を+1すればOKです♪
2-2-1:
解説
まず「172を切り捨てた百の位までの概数」を考えると、1つ下の十の位から0にした「100」でしたね。
次に切り捨てた数のゼロにしなかった部分を+1します。
「100」の「1」を+1するので「200」になります。
これが切り上げた数です。
2-2-2:
解説
まず「3647を切り捨てた十の位までの概数」を考えると、1つ下の一の位から0にした「3640」でした。
切り捨てた数のゼロにしなかった「364」の部分を+1した「3650」が切り上げた数です。
今のやり方をまとめると、こうなります。
- 指定された位の1つ下から0にして
「切り捨てた数」を出す3647→ 3640
(例)切り捨てて十の位までの概数に - 切り捨てた数の0にしなかった部分を
+1して「切り上げた数」を出す。3647→ 3640→ 3650
(例)切り上げて十の位までの概数に
切り捨てた数の出し方だけがAタイプと違います。ゼロにするのは指定の「1つ下」というのを覚えれば大丈夫ですね！
練習問題
2-1:
ヒント
ゼロにするのは指定の1つ下ですよ！
解説
❶切り捨てた数は「1724」の百の位の1つ下の十の位から0にした「1700」です。
❷ゼロにしなかった「17」を+1した「1800」が切り上げた数です。
小数の場合も同じように解きます。
2-2:
ヒント
答え方に注意して下さい。
解説
❶切り捨てた数は「17.24」の小数第1位の1つ下の小数第二位を0にした「17.20」です。
❷ゼロにしなかった「17.2」を「172」のつもりで+1した「17.30」が切り上げた数です。
答える時は最後の0は書かずに「17.3」です。
爽茶切り捨て切り上げ(Cタイプ)
爽茶切り捨て
「上から～ケタの概数にしなさい」の場合、指定+1ケタからゼロにします。
例題で確かめましょう。
3-1-1:
解説
「上から2ケタ」と指定されているので上から2+1ケタで上から3ケタ目からゼロにします。
21563の場合、21000になります。
「+1ケタ」に気をつければ簡単ですね！
切り上げ
切り上げのやり方はAタイプBタイプと全く同じで、切り捨てた数のゼロにしなかった部分を+1すればOKです♪
3-2-1:
解説
まず「21563を切り捨てた上から2ケタの概数」を考えると、上から2+1で上から3ケタから0にした「21000」です。
次に切り捨てた数のゼロにしなかった部分を+1します。「21000」の「21」を+1するので「22000」になります。これが切り上げた数です。
Cタイプの解き方をまとめると、こうなります。切り上げはABと同じです。
- 指定されたケタ+1ケタから0にして「切り捨てた数」を出す。
3647→ 3600(例)3647を切り捨てて上から2ケタの概数に
- 切り捨てた数の0にしなかった部分を+1して「切り上げた数」を出す。
3647→ 3600→ 3700(例)3647を切り上げて上から2ケタの概数に
切り捨ての時にゼロにするのは指定の「+1ケタ」からというのを覚えれば大丈夫ですね！
練習問題
3-1:
ヒント
ゼロの数をきちんと見ましょう！
解説
❶上から2+1ケタで3ケタ目からゼロにした「30000」が切り捨てた数です。
先の位の0は元々あった0です(青になっていませんね)。
❷ゼロにしなかった「30」を+1した「31000」が切り上げた数です。(40000ではありません！)
小数も試してみましょう
3-1:
ヒント
答え方に注意！
解説
❶上から3+1ケタで4ケタ目からゼロにした「2.2300」が切り捨てた数です。
❷ゼロにしなかった「2.23」を「223」のつもりで+1した「2.2400」が切り上げた数です。
答える時は最後の「00」を書かずに2.24になります。
爽茶まとめ
切り捨て・切り上げの問題は
❶切り捨てた数を出して
❷切り捨てた数から切り上げた数を出します
❶切り捨てには問題文の聞き方によって三種類の方法があります。
A「～の位を切り捨て(上げ)なさい」
→その位からゼロにする
(例)1234を十の位で切り捨て→1200
B「～の位までの概数にしなさい」
→一つ下の位からゼロにする
(例)1234を十の位までの概数に→1230
C「上から～ケタの概数にしなさい」
→上から+1ケタからゼロにする
(例)1234を上から2ケタの概数に→1200
❷切り捨てた数から切り上げた数を求めるやり方は問題文の聞き方と関係なくいつも同じで「切り捨てた数の『ゼロにしていない部分』を+1する」です。
(例)
切り捨てた数が230→切り上げると240
切り捨てた数が12300→切り上げると12400
切り捨てた数が99000→切り上げると100000
爽茶次は「がい数の総合案内」から「四捨五入」に進んで下さい。
算数が苦手な人には「陰山メソッド 徹底反復 およそのかずプリント」
歴史を学習する小学生の保護者の方へ
年表,年号,地図,書き取りテストなど400枚のプリントがセットになったそうちゃ式オリジナル教材が8/25(日)までお買い得価格！興味がある方はコチラへ
2023年度生徒さん募集
2023年度の生徒さんの募集を開始しました(対面授業の一次募集)
東武野田線・伊勢崎線沿線にお住まいの新5年生で予習シリーズをベースにされている方が対象です。
詳しくはコチラのページを御覧下さい
新4年生の方を対象に学習相談/授業を実施します(2次募集はサピックス新越谷校・南浦和校の方のみ対象。締め切り1/27)。応募はコチラから
中学受験でお悩みの方へ
爽茶「中学受験と高校受験とどちらがいいの？」「塾の選び方は？」「4年次・5年次はどう勉強すればよい？」「志望校の過去問が出来ない…」など
様々なお悩みへのアドバイスをまとめたので参考にして下さい。
もしかしたら、自分だけで悩んでいると煮詰まってしまい、事態が改善できないかもしれません。講師経験20年の「そうちゃ」に相談してみませんか？対面/オンラインの学習相談を受け付けているので、ご利用下さい。