「和差算って何?」という小学4年生や「解き方をマスターしたい」「応用発展問題を解きたい」という中学受験生の方、おまかせ下さい!東大卒講師歴20年の図解講師「そうちゃ」基本から応用・難問までを総まとめしました♪この記事を読めば和差算はもう大丈夫です。
プリント57枚全285問が無料で利用できます。目次の「プリントダウンロード」をクリックして下さい。
線分図の書き方(復習)
 爽茶
爽茶こんにちは!「そうちゃ」@zky_tutor(プロフィール)です。
和差算は線分図で習うことが多いので、あらかじめ線分図に慣れておくと良いですよ!二つの数量の関係を表す線分図は「和」「差」「比」の三種類です(図1)。「和」と「差」を組み合わせると「和」「差」算ができます(図2)
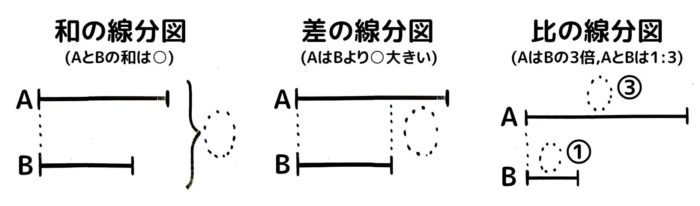
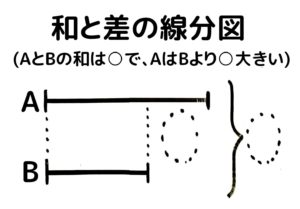
AはBより○大きい」
では、実際に線分図を使って和差算を解いてみましょう!
和差算の基本
 爽茶
爽茶和差算の基本解法
基本解法をまとめるとこうなります。
- 大小2本の線分図を書く
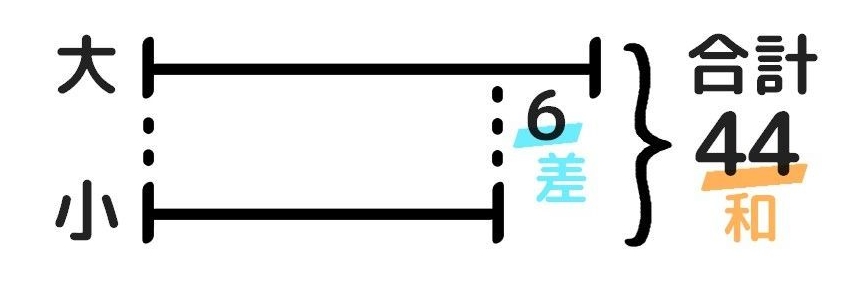
- 「小」に切りそろえる(和-差)
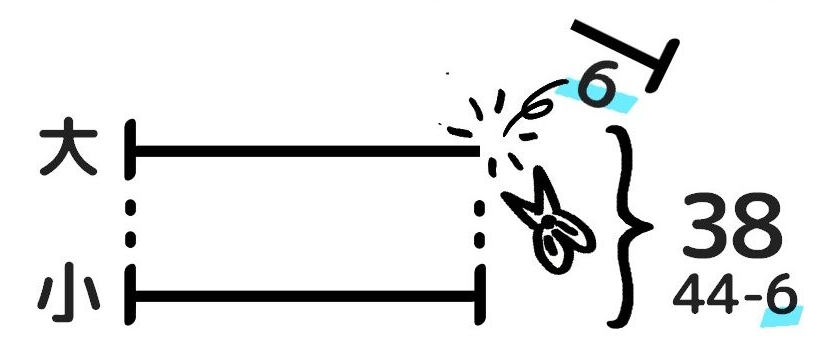
- (和-差)÷2で「小」を求める
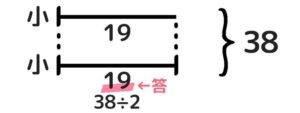
- 「小」+差で「大」を求める
練習したい人はこちらをどうぞ。
和差算の基本解法
❶線分図を書く→❷「小」に切りそろえる(和-差)→❸(和-差)÷2で「小」を求める→❹「小」+差で「大」を求める
の手順で
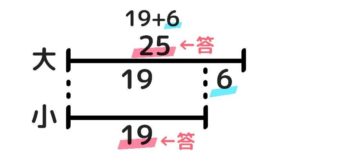
❶問題文を読むとBの方が小さいと分かるので、Aを「大」Bを「小」として線分図を書きます。そして和44と差6を書き込みます。

❷ここで「はみ出た」部分をチョキン!と切り取ります

「和-差」が小2つ分だと分かります。
❸すると、切り取った分6減って合計は38になり、これは「小」2つ分です。したがって、「小(B)」=38÷2=19 です。

❹一方「大(A)」は「小」より6大きいので、19+6=25 と分かります。
B=19
「もう少し詳しい説明が見たい」「もっと練習したい」人や、は関連記事「ちがいに目をつけて」を見て下さい。
慣れてきたら、公式一発で!
理解できたら、次は公式を使って暗算一発で出せるようにしましょう。
小が「(和-差)÷2」で求められるのは上で見ましたが、差を切り取らずに継ぎ足せば(和+差)=大2つ分になるので、大=(和+差)÷2で求められます。
「小」と「大」の和と差が分かっている時
●「小」=(和-差)÷2
●「大」=(和+差)÷2
この公式を使えば、「大」「小」どちらも一発で求められますね!
プリントダウンロード
和差算の基本問題をタップリ練習したい人に、大量18枚全90問のプリントを用意しました。zipファイルの中に問題だけのPDFと解答だけのPDFが入っているのでご利用下さい。
著作権は放棄しておりません。無断転載引用はご遠慮下さい。
ダウンロードにはパスワードが必要です。こちらからDL登録すると、このページ共通のパスワードを自動返信メールで受け取れます。
*「パスワードを入れてもダウンロードできない」という方はブラウザや使用機種を変えて再度お試し下さい
 爽茶
爽茶三つの数の和差算
 爽茶
爽茶三つの数の和差算の解き方
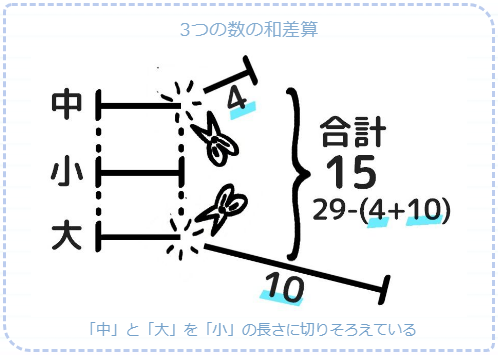
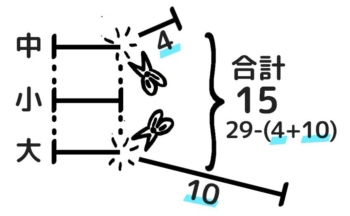
一番小さい数「小」の長さに切りそろえて解きます。
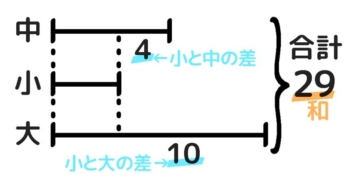
(例)ABCの和は29で、BはAより4小さくCより10小さい
- 一番小さい数「小」がどれか読み取る
- 「小」を真ん中にした線分図に、三つの合計(和)と
「大と小の差」「中と小の差」2つの差を書き込む。
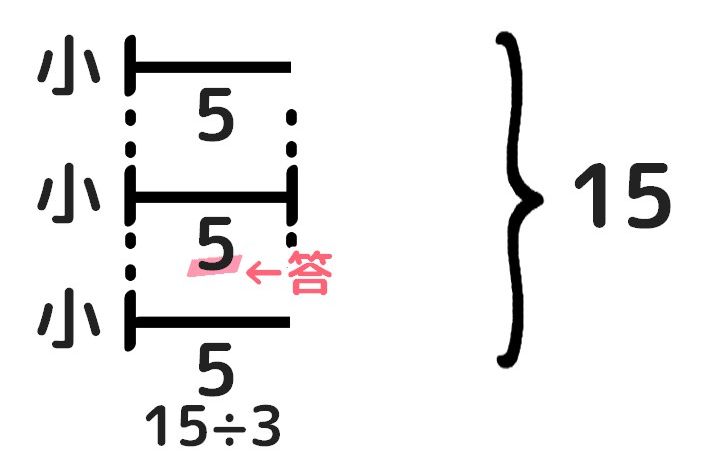
- 「小」の長さに切りそろえて、合計を減らす

- ÷3で「小」を求める。
- 「小」に差を足して「大」「中」を求める
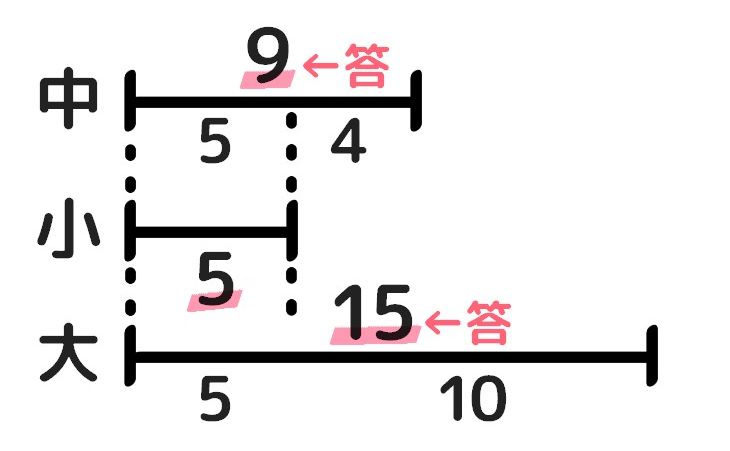
問題で確かめたい人はどうぞ
3つの数の和差算
問題文より、小さい順にC<A<Bと分かったら、一番小さいCを真ん中にした線分図を書くと、Cを基準にAは10大きくBは22大きいと分かります。
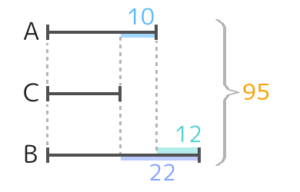
CとBの差22は10+12で求めます
あとはCの大きさに切りそろえて÷3でCを出します。
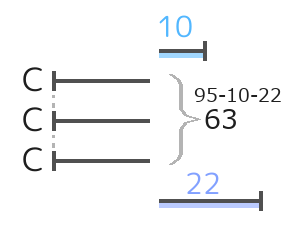
A=21+10=31,B=21+22=43と分かります。
答: A=31,B=43,C=21
もう少し詳しい説明が見たい人は「ちがいに目をつけて」内の「三つの数の和差算」を見て下さい。
プリントダウンロード
三つの数の和差算までを練習したい人のために、超大量30枚150問ものプリントを用意しました。zipファイルの中に問題だけのPDFと解答だけのPDFが入っているのでご利用下さい。
著作権は放棄しておりません。無断転載引用はご遠慮下さい。
ダウンロードにはパスワードが必要です。こちらからDL登録すると、このページ共通のパスワードを自動返信メールで受け取れます。
*「パスワードを入れてもダウンロードできない」という方はブラウザや使用機種を変えて再度お試し下さい
 爽茶
爽茶応用問題(1)
他分野との融合問題
 爽茶
爽茶摸試・受験前の復習用にまとめてみました。
平均と和差算
平均の三公式はこうでした。
●平均=合計÷人数
●個数=合計÷平均
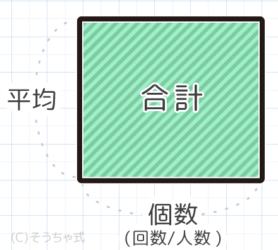
平均が分かると合計(和)も分かるので、平均算の中では和差算になるものがあります。
例えば「ABの所持金の平均が650円で、AがBより300円多い場合」なら、合計(和)が650×2=1300円、差が300円なのでこうなります。
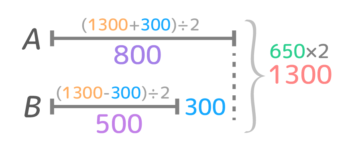
詳しくは「平均算と線分図」を見て下さい。
年齢計算の和差算
親子の年齢「差」はずっと変わらない事を利用します。
年齢の和差算
Aさんとお母さんの年齢の「差」は生まれてからずっと25歳で変わりません。
つまり現在の2人の年齢は和が43、差が25です。
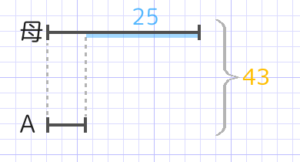
Aさん(小さい方)の年齢は(43-25)÷2=9歳と分かります。
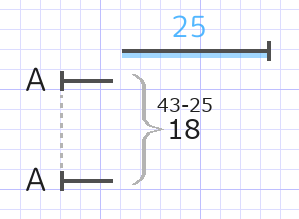
9歳
つるかめ算(個数取り違え)
二種類の品物を買い物する時に、予定と実際で買う個数を逆にしてしまった問題です。
当ブログでは面積図ではなく、線分図を使って差集め算的なアプローチで解くのをすすめています。
ちなみに差集め算の公式は以下の通りでした。
詳しく知りたい人は「差集め算」を見て下さい
取り違え問題では二番目の公式「N(個数)=差の合計÷1個の差」を使います。
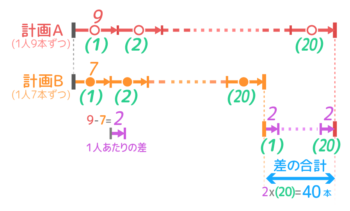
個数の取り違え
差集め算っぽい線分図を書いてみましょう
品物Aと品物Bの個数を取り違える問題の場合、
(予定金額と実際金額の差)÷(品物Aと品物Bの一個の値段の差)=AとBの個数の差 になります。
((図))
これと問題文に書いてある個数の和と合わせると和差算になります!
この問題の場合、予定金額と実際金額の差は160円、アンパンとクリームパンの一個の値段の差は120-100=20円なので、
160÷20=8個 がアンパンとクリームパンの個数の差になります。
問題文より個数の和が20個なので、
「大(もともとの個数が多い方)」「小(少ない方)」2つの数の和が20,差が8の和差算を解いて、「小」=(20-8)÷2=6 「大」=(20+8)÷2=14 と分かります
((図))
次に、アンパンとクリームパンのどちらが「小」か「大」かを考えると…
取り違えた結果高くなったので、もともとは値段が高いクリームパンの方が少なかった「小」と分かります。
よってもともとのアンパンは「大」で14個です。
答: 14個
旅人算と和差算
旅人算の基本公式から…
●出会う時間=2人の距離÷2人の速さの和
●追いつく時間=2人の距離÷2人の速さの差
出会う時間と追いつく時間が分かっている場合には速さの和と差が分かります。
●速さの和=距離÷出会う時間
●速さの差=距離÷追いつく時間
すると、速さの和と差で和差算が作れるので、2人それぞれの速さが出せます。
旅人算の和差算
速さの和と差を求めましょう
4分で出会っているので2人の速さの和=1800÷4=450m/分
36分で追いついているので2人の速さの差=1800÷36=50m/分
AとBは和450、差50の和差算(追いついているAが「大」)を解いて…
A=(450+50)÷2=250 B=(450-50)÷2=200 と分かります
答: A:250m/分,B:200m/分
流水算
流水算の船の速さは次の通りです。
●川を下る時の速さ
=静水時の速さ+川の速さ
●川を上る時の速さ
=静水時の速さ-川の速さ
(静水=止まっている水)
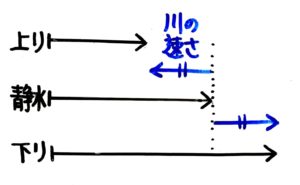
線分図だけを拡大すると下図のようになります。

これは三量の和差算と同様の関係ですね。
この図より、上る速さと下る速さが分かっていれば、静水時の速さと川の流れの速さが求められます。
●静水時の速さ=(上りの速さ+下りの速さ)÷2
●川の速さ=(上りの速さ-下りの速さ)÷2
これを使って問題を解いてみましょう。
流水算の和差算
まず上りと下りの速さをだしましょう。
行きの速さ(上りの速さ)は15÷14060=9km/時、帰りの速さ(下りの速さ)は15÷1=15km/時なので
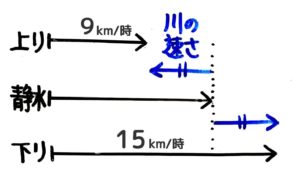
静水時の船の速さは(15+9)÷2=12km/時、川の流れの速さは(15-9)÷2=3km/時と分かります
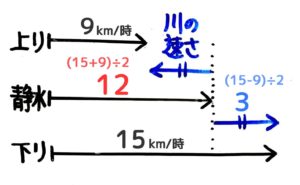
静水時の速さ:12km/時
川の速さ:3km/時
 爽茶
爽茶応用問題(2)
二重の和差算の解き方
 爽茶
爽茶「二重の和差算」というのは、こんな問題です。「三つの数との和差算」との違いが分かりますか?
3つの数ABCの合計は220である。BはCより29大きく、AはBとCの和より14大きい。ABCはそれぞれいくつか?
解き方
「まず解いている所を見たい!」人は下のスライダーを使って下さい。画像の右端をクリックすると進みます。
(例)ABCの合計は220で
AはBCの和より14大きくBはCより29大きい
- Aと「B+C」の和差算を始める
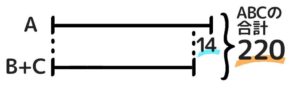
- AとB+C(BCの和)が出る。
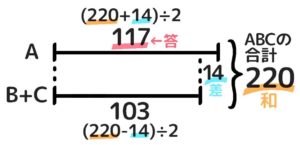
- BとCの和差算を始める
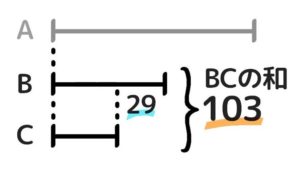
- BとCが出て、終了~♪
このやり方で、例題を実際に解いてみましょう。
二重和差算の例題
❶AとB+Cの和差算を解く→❷BとCの和差算を解く という手順で解きましょう。
❶AとB+Cの和差算を解く
「ABCの合計が220」で「AはBとCの和より14大きい」ので、BとCを別々に書かずにB+Cという一本の線分にして、AとB+Cという二本の線分で和差算と同じ図が書けますね。

これでAとB+Cの和差算を解いてA=117,B+C=103と分かります。

❷BとCの和差算を解く
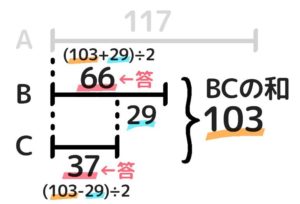
ここでB+C=103というのは「BとCの和が103」と言うことですね。
問題文より「BはCより29大きい」ので、BとCの和は103、差は29(BがCより大きい)になります。

このBCの和差算を解いて、B=(103+29)÷2=66、B=(103-29)÷2=37と分かります。

答:A=117,B=66,C=37
プリントダウンロード
二重の和差算を練習したい人のために、大量9枚のプリントを用意しました(後半は別の応用問題「疑似和差算」です)。zipファイルの中に問題だけのPDFと解答だけのPDFが入っているのでご利用下さい。
著作権は放棄しておりません。無断転載引用はご遠慮下さい。
ダウンロードにはパスワードが必要です。こちらからDL登録すると、このページ共通のパスワードを自動返信メールで受け取れます。
*「パスワードを入れてもダウンロードできない」という方はブラウザや使用機種を変えて再度お試し下さい
 爽茶
爽茶和差算の発展問題
合計が書いていない場合
 爽茶
爽茶(ここでは「疑似和差算」と読んでおきます)
疑似和差算には三種類ありますが、最後のタイプが重要です。
差が一つだけの問題
3つの数があって差が一つしか書いていないこんな問題です。
AとBの和が23、BとCの和が29、AとBの差が3である時、ABCはそれぞれいくつですか?
和差算と違って全部の合計が書いてありませんね。
よく読むか図を書くと分かりますが、AとBは和も差もかいてあります。
AとBの差が3
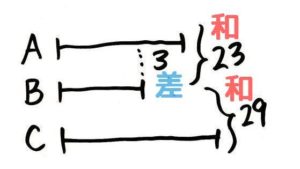
「ABの和差算にもう一つの数Cとの和がついた問題」と考えることができます。(「和差和算」と呼んでおきます)
この問題はABの和差算を解いてAとBを出して(短いBが(23-3)÷2=10と分かる)、BCの和からBを引いてCを出せばOKです。
AとBの差が3
A=23-10=13
C=29-10=19
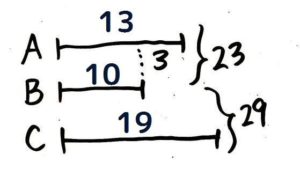
和が一つだけの問題
3つの数があって和が一つしか書いていないこんな問題です。
AとBの和が22、AとBの差が2、BとCの差が9である時、ABCはそれぞれいくつですか?
今度はAとBの「和」と「差」に加えてもう一つの数Cとの「差」が書いてあります。
AとBの差が3、BとCの差が9
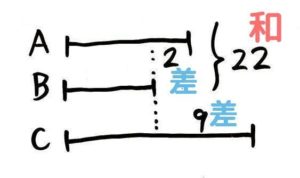
和差算にもう一つ「差」がついた問題と考えられますね(「和差差算」と呼んでおきます)
この問題はABの和差算を解いてAとBを出した後、BCの差をBに足してCを出せばOKです。
AとBの差が3、BとCの差が9
和しか書いてない問題の解き方
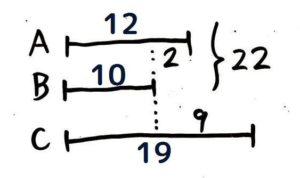
3つの数があって和しか書いていない(差が全く書いてない!)こんな問題です。
3つの数ABCがあります。AとBの和が17、BとCの和が22、AとCの和が25の時、ABCはそれぞれいくつですか?
和が3つなので「和和和算(わわわざん)」と呼んでおきます。
このタイプはよく出題されるので出来るようにしておきましょう。ただ、解き方が少し複雑です。
例題を解きながら解法を理解して下さい(2020.2.12 解法を訂正しました)。
和和和算の例題
❶和の式を並べる→❷三つの和の式から3数の合計を求める→❸三つの和の式と問題の和の式から3数を求める
❶和の式を並べる
今まで問題を読んだら(読みながら)線分図を書きましたが、「和和和算」はまず三つの「和の式」を縦に並べて書きます。
B+C=
A+C=
22
25
❷和の式の合計÷2で3数の合計を出す
三つの「和の式」を全部合計すると、「=」をはさんで左側は「A+B + B+C + A+C」になり、右側は「17+22+25」になります。
それぞれを整理すると左側は「(A+B+C)+(A+B+C)」に、右側は「64」になります。
B+C=
+) A+C=
A+B+B+C+A+C=
A+B+C+A+B+C=
22
25
17+22+25
64
(A+B+C)が2つで64なので、A+B+Cつまり3数の合計は64÷2=32 と分かりました。
(A+B+C)=
64÷2=32
❸三つの和の式と問題の和の式から3数を求める
②で求めた3つの和の式「A+B+C=32」と問題の和の式の一つ「A+B=17」を並べてみます。
A+B=17
引き算をすると、二つの式の違い32-17=15はCそのものと分かります。
- A+B+C=17
C=15
同様に、ABも求めます。
- A+B+C=22
A+B+C=10
- A+B+C=25
A+B+C=27
A:10,B:7,C:15
和しか書いていない問題(六和算)
4つの数から2つづつ選んだ和しか分からない問題です(六和算!)
X-2:六和算
ヒント
6個の和の数字の真ん中の2個がポイントです。
解説
和が6個出てきますが、このうち上2つと下2つは由来が分かります。下の2つはA+B=5,A+C=7で上の2つはB+D=10,C+D=12です。真ん中の2つはA+DかB+Cのどちらですが、どちらが8でどちらが9というのはすぐには分かりません。
((図))
A+B=5とA+C=7(またはB+D=10とC+D=12)からBとCの差が2と分かります。後はB+Cが8か9のどちらかが分かれば和差算でBとCを求められます。
ここで、差が2である2つの数の和は必ず偶数になる(詳しい説明はクリック)のでB+C=8で、和差算でB=3,C=5と分かります。
BCが分かったので、まだ使っていない式を利用してADを求めます。
A+B=5からA=2,C+D=12からD=7と分かります。
これで和差算の類似問題は終了です。
疑似和差算を練習したい人のために、大量9枚のプリントを用意しました(前半は二重の和差算です)。コチラへどうぞ。
変化する問題
これまでは、数量の関係は固定されていましたが、一度出来た数量関係が変化する場合があります。
そのような変化の問題は「分配算」の方にたくさんありますが、和差算でも問題は作れます。
例えばこういう問題です。
AとBは合わせて460円持っていたが、Aが80円使ってBは120円もらったので二人の金額は等しくなった。ABは最初いくらづつ持っていたか
変化する前と後を分けて、線分図を書きます。左端をきちんとそろえたら、あとはできるだけ単純に書きましょう
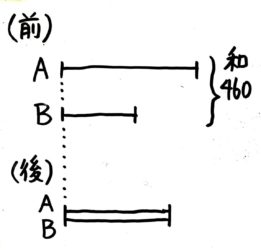
(後)の図は等しくなったことを書く。
(前)のAよりは短くBよりは長くなる。
次に「後」の線から上に向かって線を引き、使った金額ともらった金額を書き込みます。
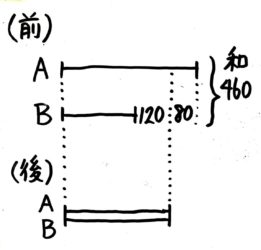
右はAが使った金額を書き込みます。
すると「前」の和と差が分かって、和差算になりました。
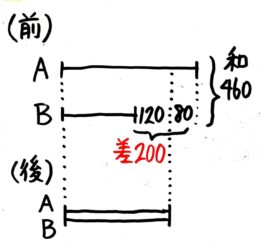
いつもの和差算でA=330,B=130と分かります。
(前)のA(大)=(460+200)÷2=130
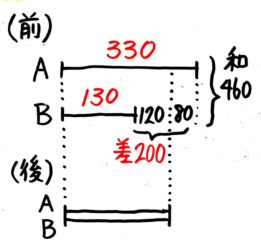
ちなみに、(後)のA=Bは130+120=250
このように「金額がそろった」場合は、無理して図をまとめず2つ書いてから、そろった図からもう一方に線を引くと考えやすくなります。
- 「前」と「後」2つの図を書く
- そろった方の線の先から、一方に線を引く
- 「スキマ」に数値を書き込み考える。
ためしに一問どうぞ。
AとBは同じ金額をもっていたが、Aが100円使って、Bが300円もらったところ、2人の合計は980円になった。はじめいくら持っていたか?
→( 図を書くと和が980,差が400の和差算になる。 )
→( 後のAは(980-400)÷2=290。Bは(980+400)÷2=690 )
→( 前のABの金額は290+100=(690-300=)390円 )
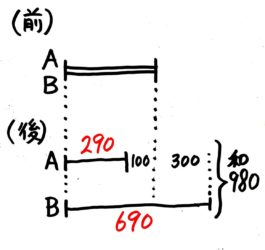 スキマに数値を書き込みます。
スキマに数値を書き込みます。これで和差算は終了です!
オススメ教材
●「和差算・分配算」(サイパーシリーズ)
●「算数の基本問題4年」(日能研)
●小4まで…和差センス(シグマベスト)
2023年度生徒さん募集
2023年度の生徒さんの募集を開始しました(対面授業の一次募集)
東武野田線・伊勢崎線沿線にお住まいの新5年生で予習シリーズをベースにされている方が対象です。
詳しくはコチラのページを御覧下さい
新4年生の方を対象に学習相談/授業を実施します(サピックス新越谷校・南浦和校・大宮校の方が対象。締め切り2/1)。応募はコチラから
中学受験でお悩みの方へ
 そうちゃ
そうちゃ受験に関する悩みはつきませんね。「中学受験と高校受験とどちらがいいの?」「塾の選び方は?」「途中から塾に入っても大丈夫?」「塾の成績・クラスが下がった…」「志望校の過去問が出来ない…」など
様々なお悩みへのアドバイスを記事にまとめたので参考にして下さい。
自分だけで悩んでいると煮詰まってしまい、事態を改善できないかもしないこともあるでしょう…
そんな時は、講師経験20年の「そうちゃ」に相談してみませんか?対面/オンラインの授業/学習相談を受け付けているので、ご利用下さい。
この記事があなたの役に立てたなら嬉しいです!