中学受験生の方「分配算」について「いろんな図を書くのが大変だなあ…」と思っていませんか?
実は線分図の書き方は基本3種類しかないんですよ!簡単でしょう?
この記事では3種類の線分図を使って分配算を解く方法を東大卒講師歴20年の図解講師「そうちゃ」が分かりやすく説明します。
記事を読みながら真似すれば分配算が得意になっているでしょう♪
この記事はけっこう長めです。
苦手な人は最初から読むのが良いですが、そうでもない人は「三量の分配算」なと読みたいところを下の目次でクリックしてジャンプすると良いですよ!
分配算の準備
 爽茶
爽茶こんにちは!「そうちゃ」@zky_tutor(プロフィール)です。
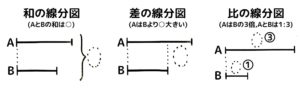
二つの数量の線分図(復習)
二つの数量の関係を表す線分図は「和」「差」「比」の三種類です。
これらの線分図が書けるか試して下さい。「↓ 開く ↓」をクリックすると答えが開きます。
1-1:三種類の線分図
解説
30
同じ長さにはしないこと!
「和」は書かなくても良いですが、カッコは書きましょう。
解説
5
点線を書きましょう
解説
➃
➀
なるべく4倍に見えるように書く
こうでしたね。
できましたか?できなかった人・詳しい説明を見たい人は関連記事「二量の関係は三つの線分図で表現できる♪」を見て下さい。
3つの線分図のうち、「和」と「差」で出来るのが「和差算」で、今回の分配算は「和」と「比」、「差」と「比」を使います。
記号数字の計算
 爽茶
爽茶分配算では記号数字(➀②など)を使った計算を行います。
この計算が素早くできれば、分配算の文章題をテンポよく解くことができますよ!
さっそく「記号計算」の練習をしてみましょう
0-2:記号数字の計算
解説
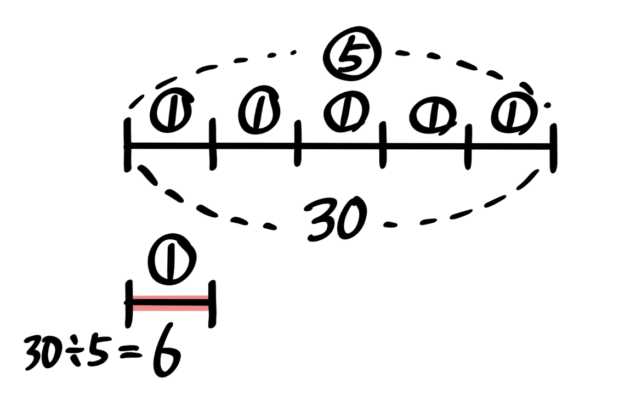
⑤の線分図と➀の線分図を縦に並べて、⑤の大きさとして30を書きます。
➀は⑤を5等分した大きさなので、➀=30÷⑤=6 と考えられます。
解説
↓
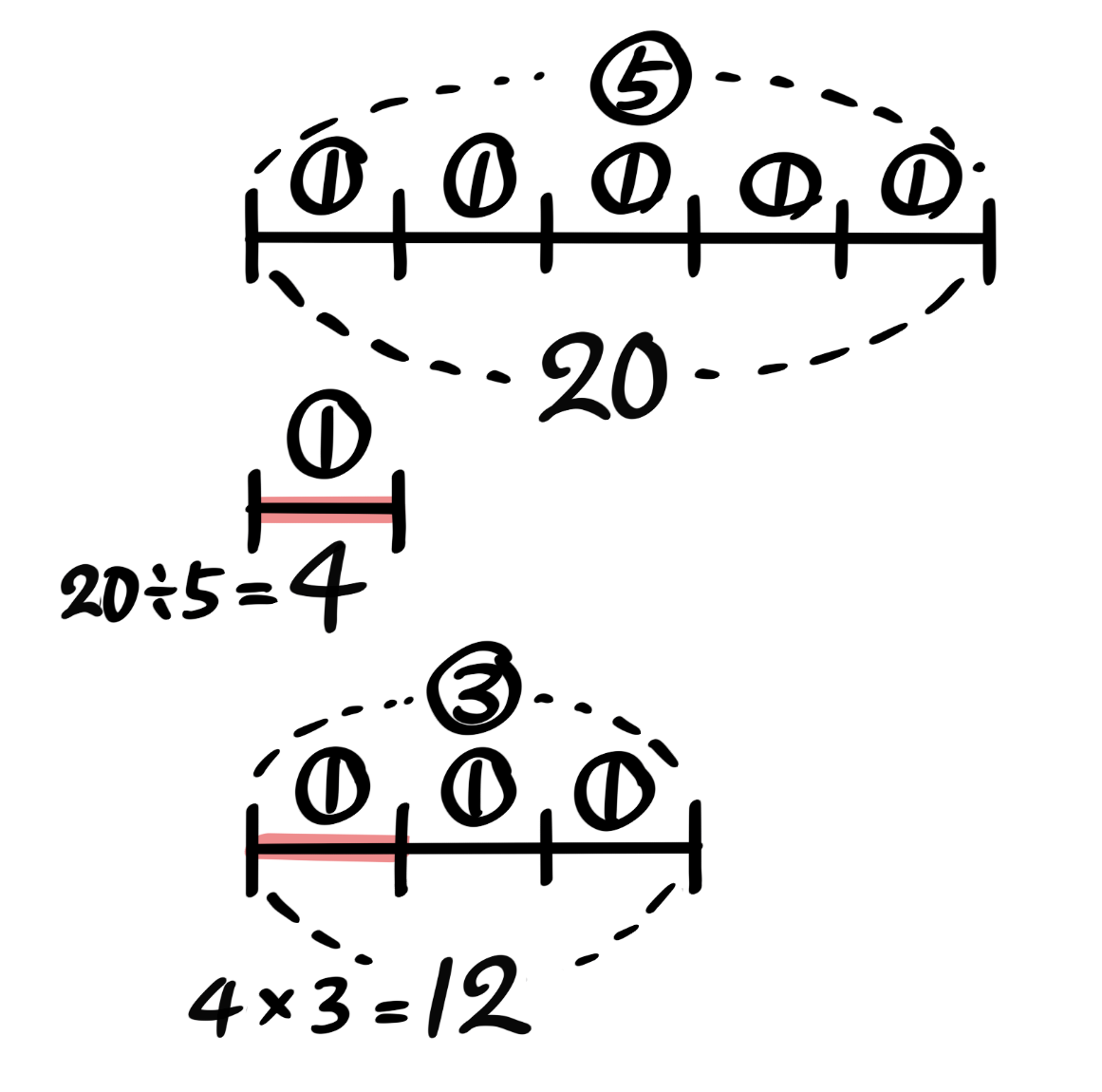
➂=4×3=12
➊➄=20 なので ➀=20÷5=4 と分かる
➋➂は➀の3倍なので➂=4×3=12
このように「丸数字=普通の数」という関係が見つかったら、「普通の数÷丸数字」を計算して➀を出して下さい。
そして、この先は図を書かず暗算で出来るようにしておきましょう。確認テストをどうぞ。
0-2:記号数字の計算
解説
⑤=12÷③×5=20
このように一発で計算して下さい。
解説
❹=56÷❼×4=32
解説
➉=36÷6×10=60、➎=33÷❸×5=55 →➉+➎=60+55=115
できましたか?
小まとめ
「和」「差」「比」の三種類がある
→「丸数字=普通の数」という関係を見つけたら、
普通の数÷丸数字で➀を求めて利用する
(例)➅=24の時、⑪は?
→ 24÷➅=4=➀ → ⑪=4×11=44
和と比の分配算
 爽茶
爽茶ピッタリ倍(端数が無い)の場合
まず「2倍」「3倍」のようなピッタリ倍の場合の例題を解いてみます。
➂
➀
88=④
↓
➀=22
2つの線分図A➂とB➀と和88を書きます。
AとBの和は丸数字で➂+➀=➃とも表せるので「88=➃」と分かります。
「丸数字=普通の数」が分かったので➀を88÷➃=22と出せば、A➂=22×➂=66、B➀=22が答え。
ここでも丸数字と普通の数(数値)をイコールで結んだ関係を見つけるのが大切です。
- 線分図を書き「丸数字=数値」になっているところを見つける。
- 「数値÷丸数字」で➀の大きさを出す
- ➀を何倍かして答えを求める
類題で定着させましょう。
1-1:和比分配算
解説
➃
➀
85=➄
↓
➀=17
➃=17×➃=68(A)
解説
➀
⑫
117=⑬
↓
➀=9
⑫=9×⑫=108(B)
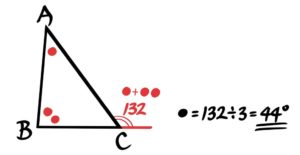
分配算は図形問題でも出ることがあります。
1-2:図形との融合
解説
角Cの外角が132°。角A?」
解説
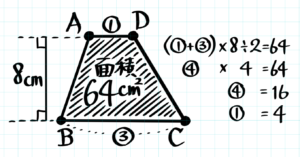
上底を➀下底を➂として台形の面積の公式を作れば丸数字の計算になりますね。
次はピッタリ倍でない場合です。
端数がある場合
例えば「AはBの3倍より4大きく…」のようにピッタリ「○倍」ではない場合、一瞬とまどうかもしれません。
焦らずに、とりあえず端数を含めた全ての数字を線分図に書きましょう。
それから落ち着いて観察し「丸数字=数値」を見つけるか、考えます♪
プラスの端数
例題で解き方を理解しましょう。
➂
➀
➃+4=56
↓
➃=52
Bは➀、AはBの3倍より4大きいので➂ではなく「➂+4」、AとBの合計も➃ではなく「➃+4」になり、これが56になります。
➃+4=56 なので➃=56-4=52と分かります♪
あとはピッタリ倍の時と同様に、➀=48÷4=12(B) 、➂=12×3=36、A=➂+4=36+4=40 とが答えです。
例題でAは➂ではありません!➂=36を出したときにA=36と書かないように注意しましょう。そのためには、36が出たら自分の図に書き込むのがコツです。
➂
➀
➃+4=56
↓
➃=52
問題を読んだら図に数値を書き込んで考えるヒントにします。
また、計算して出した数値は必ず図に書き込みましょう。
そうすれば自分でミスに気づくことができます。
このように図は情報の集約装置の役割があります。
マイナスの端数
端数がマイナスの場合、図が少し難しくなります。例題を解いて下さい。
➂-7
➀
➃-7=113
↓
➃=120
できればピッタリ3倍の線分を一番上に合計3本の線分を書くのが良いです。
そして2つの線分A➂-7とB➀との和113を書きます。
➃-7=113から➃=113+7=120 と気づけば後は簡単です。
➀(B)=120÷4=30、➂=30×3=90、A=➂-7=90-7=83 が答え。
線分図を3本書きましたが、この問題を解くだけなら2本でも構いません。(後で出てくる線分図の問題を考えると3本引くことに慣れてほしいのですが…)
➂-7
➀
➃-7=113
↓
➃=120
類題で定着を確認して下さい。
2:和比分配算(端数)
解説
➃
➀
➄+7=112
↓
⑤=105
➀=105÷⑤=21(B)
A=21×➃+7=91
解説
➃-9
➀
⑤-9=86
↓
⑤=95
➀=95÷⑤=19(B)
A=19×➃-9=67
以上で「和」と「比」の分配算は終了です。次は「差」と「比」の分配算です。
 爽茶
爽茶差と比の分配算
 爽茶
爽茶ピッタリ倍(端数が無い)の場合
「和」と「比」の分配算とほぼ同じですが、違いに気をつけて解いてみましょう。
➂
➁=12
➀
線分図A➂とB➀に加えて、今度は「差」を書き込みます。差が分かりやすいように点線を書きます。
AとBの差12は丸数字で➂-➀=②とも表せるので「12=②」と分かります。
➀=12÷②=6(B)、A➂=6×➂=18 が答えです。
類題で定着させましょう。
⑤
➃=64
➀
A=16×⑤=80
➀
⑧=126
➈
B=14×➈=126
次は「差」「比」で端数がある場合です
端数がある場合
プラスの端数
同じ様に線分図にしてみましょう。
➂
➁+4=22
➀
➁=22-4=18と分かる
Bは➀、Aは➂+4です。そして差は➁+4でこれが22と等しくなります。
➁=22-4=18と分かります。
➀は18÷➁=9(B)で、A=➂+4=9×➂+4=31 が答えです。
ここでも➂がAで無いことに注意しましょう。
マイナスの端数
図が少し面倒ですが…
➂-3
➁-3=23
➀
➁=23+3=26と分かる
できればピッタリ3倍の線分➂を一番上にして3本の線分を書きます。Aは➂より3短い線分です。そしてABの差が23なので➁=23+3=26とわかります。
あとは ➀=26÷➁=13(B)、A=➂-3=13×3-3=36 が答えです。
理解できたら、類題で定着を確認して下さい。
差が105」
➅
⑤+5=105
➀
➀=100÷⑤=20(B)
A=➅+5=20×6+5=125
差が114」
➆-18
➅-18=114
➀
➀=132÷➅=22(B)
A=➆-18=154-18=136
これで分配算の基本は終了です。次は三つの数字の分配算です。
 爽茶
爽茶三量の分配算
 爽茶
爽茶少し面倒くさいですが考え方は一緒です。
和と比と比
前置の文章。
ABCの合計は48」
➂
➁
➀
➅=48
↓
➀=8
問題をよく読んで、一番小さい人を➀とします。この問題ではCが➀Bは➁Aは➂です。3つの線分図と和48を書きます。
合計は➀+➁+➂=➅とも表せるので➅=48です。
➀=48÷➅=8(C)、B=➁=8×2=16、A=➂=8×3=24 が答えです。
一番小さい量を➀とおいて、残りの量を表す。
例題のように端数が無いピッタリ倍の時は計算だけでも解けますが、端数がある場合は線分図を書いて考えた方がミスがへるでしょう。
確認テストをどうぞ
一番小さいAを➀とおくと、Bは➂でCは➃。合計は➇でこれが264と等しい
➇=264だから➀=264÷8=33(A)、B=➂=33×3=99、C=➃=33×4=132
一番小さいBを➀とすると、合計はB➀+A➂+C➅で➉
➉=1200 なので➀=1200÷10=120(B)、A=➂=120×3=360,C=➅=120×6=720
AはCの3倍より4少なく、BはCの2倍より5大きい。ABCの合計が79であるとき、ABCを求めよ。
BはCの2倍より5大きい。
ABCの合計が798」
➂-4
➁+5
➀
➅+1=79
↓
➅=78
単純な足し算だと分かるので省略形で三本の線分図を書く。
一番小さいCを➀に、Aは➂-4、Bは➁+5と表せるので、合計の79は➀+(➁+5)+(➂-4)=➅+1と等しい
➅+1=79より➅=79-1=78と分かる
➀=78÷6=13(C)、B=➁+5=13×2+5=31、A=➂-4=13×3-4=35 が答え
小問の解説文章。
できましたか?
差と比と比
線分図を書けば…
BとCの差は12」
④
➂
②=12
➀
BとCの差12=➁ と分かる
BとCの差12=➁ と気付きます。後は今まで通り、➀(C)=12÷2=6、➂(B)=6×3=18、④(A)=6×4=24 と分かります
CはAの3倍、BはAの5倍、BとCの差は380の時、ABCは?
→( 一番小さいAを➀とおくとCは➂,Bは➄で、BとCの差は➁ )
→( ➁=380だから➀=380÷2=190 )
→( A=190,C=190×3=570,B=190×5=950 )
端数あり
→( 2019.11.18作成中 )
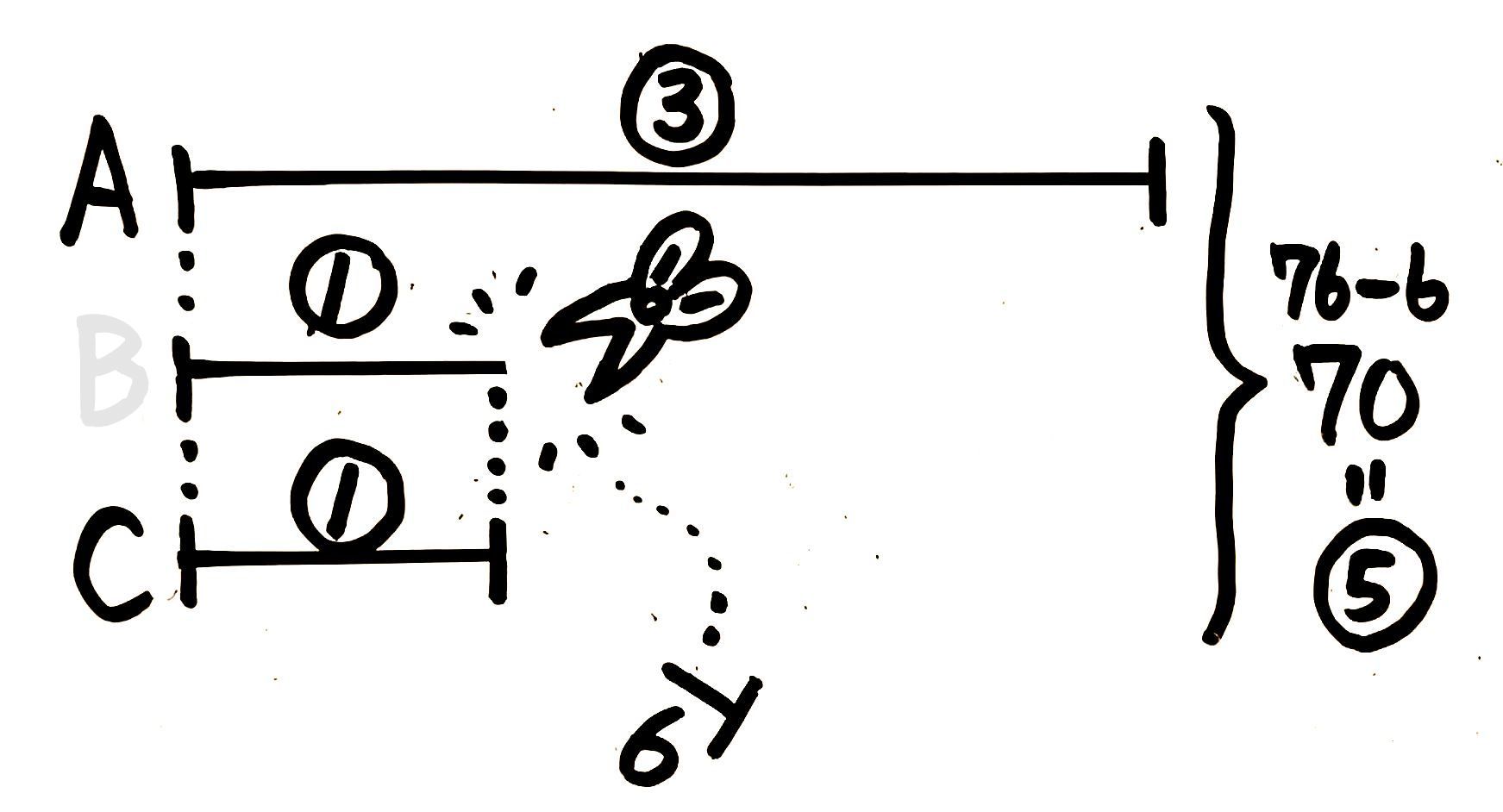
和と差と比
とりあえず線分図を書きましょう。
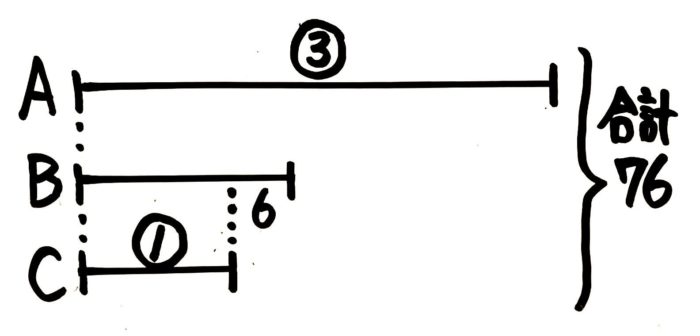
「数値=丸数字」になっている箇所がないのでどうするか考えます。2つの考え方があります。
1つ目の考え方は「和差算」風です。Bから差の6を切り取って➀にすれば、合計も76から70に減って、この70=➄と分かります。
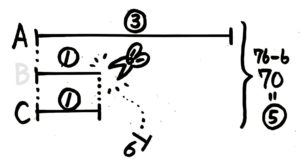 余分を切り取ってしまえば、
余分を切り取ってしまえば、線分が全部丸数字になります。
真ん中の線はBでは無くなります。
2つ目の考え方は、Bのところに「➀+6」と書き込んで合計を「⑤+6」とすれば「⑤+6=76」になるので⑤=76-6=70と出すものです。どちらかというと「数字が好き」な生徒向けです。
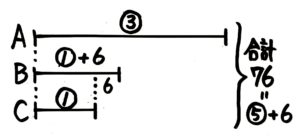 76=⑤+6 から ⑤=70と分かる
76=⑤+6 から ⑤=70と分かるこのブログとしては1つ目の考え方をすすめます。私の経験上、算数が苦手な生徒にとっては「丸数字にそろえる」という統一方針を覚える方が安心できるからです。
いずれにしろ、⑤=70と分かった後は今まで通り、➀(C)=70÷5=14、B(➀+6)=14+6=20、➂(A)=14×3=42 と分かります。
AはBの4倍でCより13大きく、ABCの合計は113の時、ABCは?
→( Bを➀とおくと、A=④,C=④-13 )
→( Cに13を足して④にすると、合計は➀+④+④=⑨で、これが113にも13を足した126と等しい )
→( ⑨=126から➀=126÷9=14 )
→( B=14,A=14×4=56,C=56-13=43 )
端数2つあり
→( 2019.11.18作成中です )
 爽茶
爽茶様子が変化する問題
 爽茶
爽茶変化する問題は「変化しないのは何か」を考えて解きます。
主に3つの場合「差が変わらない」「和が変わらない」「前か後が等しい」があります。
「差」が変わらない問題
変化する量が等しい場合
例えば「Aは900円、Bは700円持っていた。2人が同じ金額を使ったところ、AはBの2倍になった。2人はいくら使いましたか?」という問題です。
「変化前」「変化後」の2つの図を書き、差が等しいことに注目して解きます。
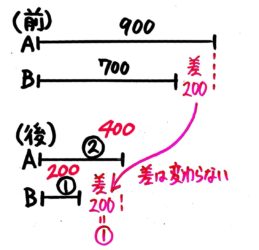
詳しい説明を見たい問題を解きたい人は「年齢算や差が等しい問題」を見て下さい。
時間の経過(年齢算)
例えば「現在、A君は8歳でお父さんは38歳です。お父さんの年齢がA君の2倍になるのは何年後ですか?」のように、時間が経過することで二人の年齢の「比」が変化する問題を「年齢算」と言います。
二人の年齢の「差」は何年経っても変わらないので、上で解いた「変化の量が等しい」問題と同様に解けばOKです。
例題では、現在のA君とお父さんの年齢差38-8=30はずっと変わらないので、?年後のA君の年齢が➀、お父さんの年齢が➁で二人の差➀=30と分かります。
変化が分かるように
横に並べて書くことも多い。
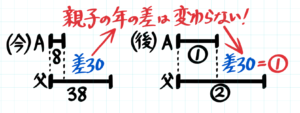
➀30=?年後のA君の年齢なので、これは30-8=22年後!と分かります。
→二人の年齢差は変わらないことを利用して、
「差と比の分配算」として解く
例
詳しい説明を見たい問題を解きたい人は「年齢算や差が等しい問題」を見て下さい。
変化の前か後が等しい問題
例えば「Aは1020円、Bは480円を持って店で買い物をしたら2人の残り金額が同じになった。AがBの4倍のお金を使った時、Aが使った金額はいくらか?」という問題です。
上の問題と違い、2人が使った金額が違うので「差が等しい」は使えません…とりあえず「前」と「後」の図をかき始めます。
分かることをシンプルに書く
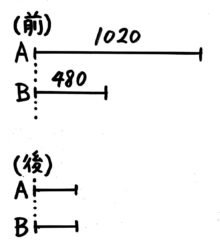
Aが使った金額がBの4倍が少し難しいですが、こう書けばよいでしょう。
「後」から「前」に線を引くと…
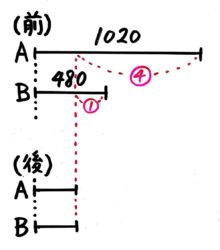
これで「前」の二人の差540=➂ と分かりますね
「差と比」の問題になって
➂=540 と分かりました!

あとは今までと同じように、➀(Bが使った金)=540÷3=180円、④(Aが使った金)=180×4=720円と分かります。(ちなみに残った金額は300円です)
「後(残り)」が同じ場合、「前」に線を引いて区切ると「差と比」の問題になる
AはCの 倍、BはCより 大きく、ABCの合計は の時、ABCは?
→
端数あり
→
和が等しい問題
やりとり算
例えば「仲良しのABC三人が36個のアメをテキトーに分けた後、6個しか持っていないBに対してAが4個、Cも何個かのアメを分けてあげたらABCのアメの数がぴったり同じになった。はじめABCは何個ずつ持っていましたか?」のような問題です。
この問題には2つの特徴があります。➊アメの合計(和)がずっと36個で変わらない ➋最後は3人が等しくなる
線分図ではなく「やりとり図」を書いて解きます。関連記事「やりとり算の解き方」を見て下さい。

ワリカン算
例えば「AB2人で遊びに行って、飲み物売り場でAが二人のジュース代400円を払い、チケット売り場ではBが二人のチケット代2000円を払った」場合、代金の総額2400を÷2(割り勘といいます)した1200円が一人分の代金なので、Aは800円払い足りずBは800円払い過ぎです。そこでAがBに800円払います。これを「清算」といいます。
このような「精算」も二人の間でお金のやり取りをするので「やり取り算」と似ていますが、解き方(図)が異なるので当サイトでは「ワリカン算」と呼ぶことにします。
「ワリカン」算の解き方は関連記事「やりとり算の解き方」を見て下さい。
変化する分配算は以上です。
小数・分数倍の比(小5)
関連記事「[作成中]小数・分数を使った分配算」を見て下さい。
 爽茶
爽茶●分配算をたくさん解きたい人には「和差算・分配算」(サイパーシリーズ)
●他の単元も復習したい小6には「算数ベストチェック」(日能研)
●単元学習中の小4・小5には「算数の基本問題4年」(日能研)
歴史の点数を上げたい受験生と保護者の方へ
年表・年号・地図・書き取りテストなど400枚のプリントがセットになった歴史教材で模試入試対策♪ 興味がある方はコチラへ
2023年度生徒さん募集
2023年度の生徒さんの募集を開始しました(対面授業の一次募集)
東武野田線・伊勢崎線沿線にお住まいの新5年生で予習シリーズをベースにされている方が対象です。
詳しくはコチラのページを御覧下さい
新4年生の方を対象に学習相談/授業を実施します(サピックス新越谷校・南浦和校・大宮校の方が対象。締め切り2/1)。応募はコチラから
中学受験でお悩みの方へ
 そうちゃ
そうちゃ受験に関する悩みはつきませんね。「中学受験と高校受験とどちらがいいの?」「塾の選び方は?」「途中から塾に入っても大丈夫?」「塾の成績・クラスが下がった…」「志望校の過去問が出来ない…」など
様々なお悩みへのアドバイスを記事にまとめたので参考にして下さい。
自分だけで悩んでいると煮詰まってしまい、事態を改善できないかもしないこともあるでしょう…
そんな時は、講師経験20年の「そうちゃ」に相談してみませんか?対面/オンラインの授業/学習相談を受け付けているので、ご利用下さい。
この記事があなたの役に立てたなら嬉しいです!
保管セクション
分子と分母の比が3:5
1
⑧=56
↓
➀=7

詳しく
保管セクションここまで