「約数が何個あるのかパッと出したい!」という中学受験生や中学生の方、おまかせ下さい!東大卒講師歴20年の図解講師「そうちゃ」が分かりやすく図解します!読み終わる頃には約数の個数が暗算で出せるようになりますよ♪
素因数分解が分からない人は参考記事「約数倍数のまとめ」内「素因数分解」を見て下さい。
約数の個数を求めるには
書き出しだと限度がある!
こんにちは!「そうちゃ」@zky_tutor(プロフィール)です。
「約数の意味」では約数を「書き出し法」で求めました。覚えているか(知っているか)テストしてみましょう。
●復習例題
「A×B」の形に直せれば、AとBが約数です。
12を2つの数のかけ算にすると「1×12」「2×6」「3×4」に直せます。
以上より12の約数は1,2,3,4,6,12の6つです。
6個
このように書き出せば、どんな数でも約数の個数を求めることができます。
ただ…数が小さいうちは良いのですが、大きな数、例えば「1050」のような4ケタの数になったりすると…
1×1050
2×525
3×350
4×…
(+_+)ムリ!となります
ところが!ある方法を使えば、数え上げなくても約数の個数が分かってしまうのです!
例えば、1050でしたら、因数分解すると「2×3×5×5×7」になります。これを見て…2×2×3×2=24個!と3秒で分かってしまうのです
今回はその方法を練習をしましょう!
素因数分解を使う
約数の個数の求め方
(例:12の約数の個数)
素因数分解から約数の個数が分かるのは、約数は素因数から出来ているからです。
説明
12=2×2×3 を例に説明します(長いので興味がある人だけ読んで下さい。問題を解けるようになるのが最優先です)
[su_spoiler title=”長い説明を読む” style=”fancy” open=”no” icon=”chevron-circle” class=”std no-trn pale”]
約数は素因数から出来ている…の?
最初に約数を6個と出した「12」を「二分解法」で12を素因数分解してみます。
12→2×6→2×2×3 または 12→3×4→2×2×3 でしたね。
これを見ると、12の約数は2,3はもちろん、4や2×2、6は2×3、12は2×2×3 と皆「2」と「3」でできているのが分かります
つまり、約数は素因数の組み合わせでできている?気がします!!
( ・`ω・´)
ただ…もう一つ約数がありますね?
1 です。
1を2や3からは作れないように見えます困った…
(^_^;)
1を作るには…
もう一度、12の素因数分解をみましょう
12=2×2×3です
この「2」「2」「3」を使ってかけ算で好きな数を作るというのを、2を赤い玉●3で、3を青い玉●に例えると、
●●と●を自由に組み合わせると何通り作れるか,という問題と同じですね。
何通りでしょう?
①●
②●●
③●
④●●
⑤●●●
で、5通り!そう思った人、惜しい!です
もうひとつ、⑥(何も無し)というのがあります。
「自由に」はそういう意味でした
(^_^;)
コレを表にすると、こうなります。
| ●の要素(→) ●の要素(↓) |
無し | ● | ●● |
| 無し | ⑥(何も無し) | ①● | ②●● |
| ● | ③● | ④●● | ⑤●●● |
つまり、●は3パターン、●は2パターン
それをかけ合わせて3×2=6 なので 6通りある、という仕組みです。
ここで、話を素因数分解に戻します。
今の表の●●を「2」「3」にするとどうなるでしょうか?
●は2,●●は2×2、●は3 これは良いですね?
問題は「無し」です。
| 2の要素(→) 3の要素(↓) |
??? | 2 | 2×2 |
| ??? | |||
| 3 |
ここで、因数分解の時に、いつも仲間はずれにされていたカワイソウな数字「1」の出番です!
かけ算では、1はあってもなくても同じ数字なので、「無し」の代わりに1を使いましょう。
表を書くと、こうなります
| 2の要素(→) 3の要素(↓) |
1 | 2 | 2×2 |
| 1 | 1×1=1 | 1×2=2 | 1×2×2=4 |
| 3 | 3×1=3 | 3×2=6 | 3×2×2=12 |
12=2×2×3 から
「2」が2個なので「2」は2+1=3パターン
「3」が1個なので「3」は1+1=2パターン
(無しの「1」の分が+1されます)
3パターン×2パターン=全部で6パターン になります
これで、12の素因数分解「2×2×3」から12の約数を6個導くことができました!![/su_spoiler]
まとめと公式化
というわけで「12=2①×2②×3① と因数分解できるので、12の約数の個数は(②+1)×(①+1)=3×2=6 と求めることができると分かりました。
12は「2」と「3」の二種類の素数しか出てきませんでしたが、三種類以上の素数が出てくる場合も同じように出せます。
例えば60=2×2×3×5の場合
「2」が2個なので(2+1)パターン
「3」が1個なので(1+1)パターン
「5」が1個なので(1+1)パターン
合計で(2+1)×(1+1)×(1+1)=12パターン
60の約数は12個と出せます。
まとめると…こうなります。
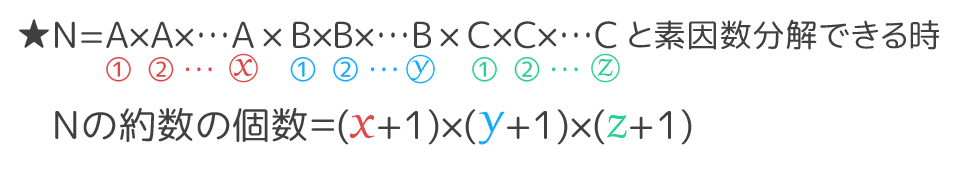
では、練習してみましょう!
●類題1-1
100を素因数分解すると
[su_spoiler title=”どうなりますか?” style=”fancy” icon=”chevron-circle” class=”std no-trn pale”]
2) 50
5) 25
5
2×2×5×5 です
「2」が2個「5」が2個なので、約数の個数は
[su_spoiler title=”何個ですか?” style=”fancy” icon=”chevron-circle” class=”std no-trn orange”]
(2+1)×(2+1)=9個ですね
答: 9個[/su_spoiler]
●類題1-(2)
[su_spoiler title=”解答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn pale”]
126を素因数分解すると
3) 63
3) 21
7
2×3×3×7 です
「2」が1個「3」が2個「7」が1個なので
約数の個数は(1+1)×(2+1)×(1+1)=12個です
答: 12個[/su_spoiler]
●類題1-(3)
はじめに出てきた「1050」の種明かしです
[su_spoiler title=”解答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn pale”]
素因数分解すると
3) 525
5) 175
5) 35
7
2×3×5×5×7 です
「2」が1個「3」が1個「5」が2個「7」が1個なので
約数の個数は、(1+1)×(1+1)×(2+1)×(1+1)=24個です。
答: 24個
こうやって簡単に出していたんですね![/su_spoiler]
●類題1-(4)
[su_spoiler title=”解答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn pale”]
素因数分解すると
2)16
2) 8
2) 4
2
2×2×2×2×2 です
「2」が5個なので、約数の個数は (5+1)=6個です
答: 6個
32のように、素因数が一種類しかない場合は掛け算が出来ないので、そのまま答えになります。[/su_spoiler]
 爽茶
爽茶これで約数の個数の求め方は終了です。公式一発で得点できるので、必ず身につけて下さいね!
逆向きの問題
公式(素因数分解から約数の個数を出す)の逆に、約数の個数から素因数分解の形を求める問題
例「1から50までの数のうち、約数が3つのものは何個あるか?」
→素因数分解すると「a×a」(素数の平方数)という形は、約数が(2+1)=3個になる。(この形以外には無い)
→1から50までに素数の平方数は「2×2=4」「3×3=9」「5×5=25」「7×7=49」の4個。
例2「 〃 、約数が4つのものは何個あるか?」
→約数が4つあるのは「a×b」(X型)か「a×a×a」(Y型)
→数え上げると…
→X型は「2×3」~「2×23」の8個+「3×5」~「3×13」の4個+「5×7」の1個=13個
→Y型は「8(2x2x2)」「27(3x3x3)」の2個のみ
→合わせて13+2=15個
まとめると…
●約数が1個の数→「1」だけ
●約数が2個の数→素数
●約数が3個の数→素因数分解すると「AxA」の形になる数(素数の平方数)
●約数が4個の数
→素因数分解すると「A×B」または「A×A×A」の形になる数
(例)20までの整数で約数が4個の数
→「A×B」形は6(2×3),10(2×5),14(2×7),15(3×5)
「A×A×A」形は8(2×2×2)で、合計5個
●約数が5個の数
→素因数分解すると「A×A×A×A」の形になる数
●約数が6個の数
→素因数分解すると「A×A×B(A×B×B)」または
「A×A×A×A×A」の形になる数
まとめ
約数の個数(素因数分解利用)
(例1)12の約数の個数
→→12=2×2×3(2が❷回、3が❶回)
→→12の約数は(❷+1)×(❶+1)=2×3=6個
(例2)90の約数の個数
→→90=2×3×3×5(2❶回、3❷回、5❶回)
→→90の約数は(❶+1)×(❷+1)×(❶+1)=2×3×2=12個
 爽茶
爽茶→(公)約数/倍数のまとめに戻る
●
2023年度生徒さん募集
2023年度の生徒さんの募集を開始しました(対面授業の一次募集)
東武野田線・伊勢崎線沿線にお住まいの新5年生で予習シリーズをベースにされている方が対象です。
詳しくはコチラのページを御覧下さい
新4年生の方を対象に学習相談/授業を実施します(サピックス新越谷校・南浦和校・大宮校の方が対象。締め切り2/1)。応募はコチラから
中学受験でお悩みの方へ
 そうちゃ
そうちゃ受験に関する悩みはつきませんね。「中学受験と高校受験とどちらがいいの?」「塾の選び方は?」「途中から塾に入っても大丈夫?」「塾の成績・クラスが下がった…」「志望校の過去問が出来ない…」など
様々なお悩みへのアドバイスを記事にまとめたので参考にして下さい。
自分だけで悩んでいると煮詰まってしまい、事態を改善できないかもしないこともあるでしょう…
そんな時は、講師経験20年の「そうちゃ」に相談してみませんか?対面/オンラインの授業/学習相談を受け付けているので、ご利用下さい。
この記事があなたの役に立てたなら嬉しいです!

