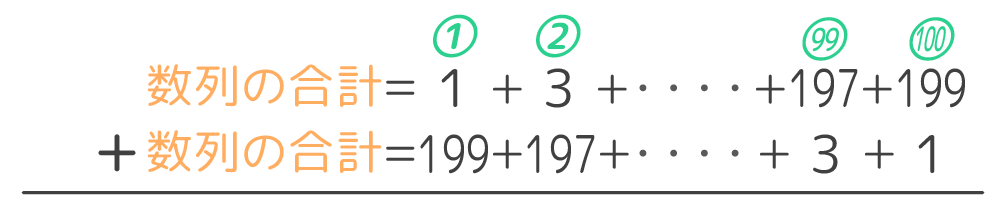「等差数列の数列の和の出し方が良く分からない…」とお悩みの中学受験生の方、もう大丈夫ですよ!東大卒講師歴20年の図解講師「そうちゃ」が分かりやすく教えます。これを読めば数列の和は得意になりますよ!
下の目次から好きな箇所にジャンプできます。問題を解きたい人は「問題を解く」を、プリントをダウンロードしたい人は「プリントダウンロード」をクリックして下さい。
等差数列の基本(復習)
 爽茶
爽茶こんにちは!「そうちゃ」@zky_tutor(プロフィール)です。
等差数列は「『はじめの数』から『等しい差(公差)』で増えていく数の並び」でした。
基本図と公式を見て思い出して下さい。
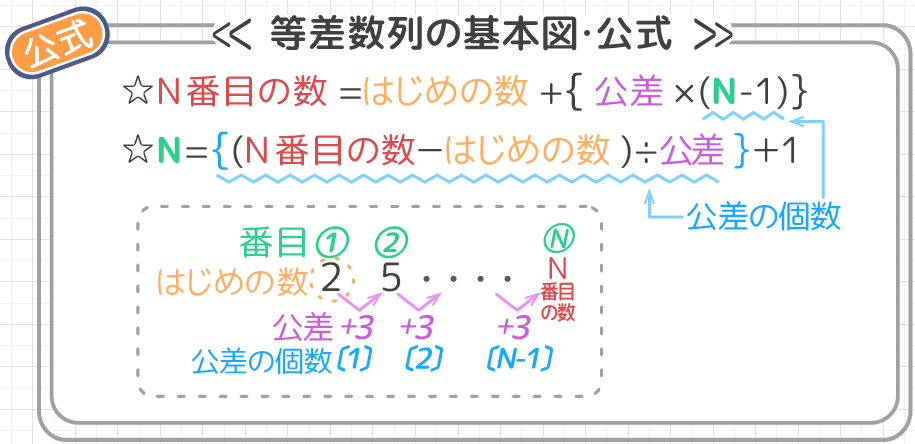
特に最初の「N番目の数」の公式が大事なので、確認テストをしてみましょう。
0-1:等差数列のN番目
解説
はじめの数=2、公差=3、N=100だから、
100番目の数=2+{3×(100-1)}=299
出来ましたね!?
 爽茶
爽茶等差数列の和の公式を求める
数列の和
「等差数列の和」というのは数列の「はじめの数」から何番目かの数までを全部足したものです。
例えば「2,5,8…という数列の1番目から5番目までの和」なら、「2,5,8,11,14」を合計して2+5+8+11+14=40 となります。
今のように5個の数の和なら単純に足せば良いのですが、「100番目までの数の和」になると計算(公式)で求めないと無理ですね。
ここでは三種類の求め方(公式)を順に紹介します。
❶「ペア」式
❷「逆二段」式
❸「台形」式
公式は知ってる・分かるという人は問題へジャンプして下さい
2つをセットにする「ペア式」
低学年の生徒さんや、数や図形が苦手な生徒さんでも直感的に分かりやすいのが「ペア式」です。
例題1(ペア式)
まず、最初の「1」と最後の「19」をペア(一組)にします。和はいくつですか?
1+19=20ですね。
次に、2番目の「3」と最後から2番めの「17」をペアにします。今度の和はいくつですか?
3+17で、また20です。
さらに、3番目の「5」と最後から3番目「15」をペアにします。和はいくつですか?
5+15なので、またまた20ですね。しつこくてゴメンナサイ…
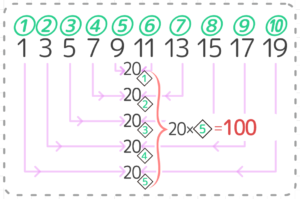
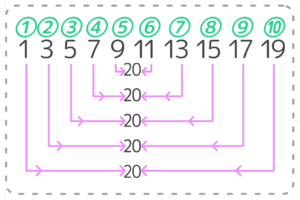
このように10個の数字全部をペアにしていくと、それぞれの和はどうなるでしょうか?また、何ペアできるでしょうか?
予想できたと思いますが、全てのペアが20になります。そして、10個の数字を2個ずつペアにするので、全部で10÷2=5つのペアが出来ます(図2)。
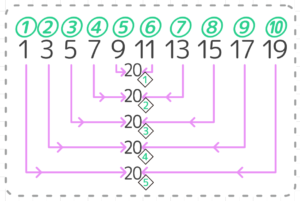
面白いよね?(^_^;)
したがって、10個の数字の合計はいくつでしょうか?
このように、等差数列の合計(和)は、ペア数字の和✕ペアの個数で求められます。
等差数列の和=ペアの和×ペアの数
「ペアの和」は、どのペアを選んでも同じなので、分かりやすいように「はじめの数と最後の数」で代表させましょう。
そして「ペアの個数」は10÷2 つまり「数字の個数÷2」でしたので、こういう公式ができます。
等差数列の合計
=(はじめの数+最後の数)✕数字の個数÷2
(例)等差数列 ①1 ②3 ③5 … ⑩19 の和は?
→(1+19)×⑩÷2=100
今の問題は数字が10個しかありませんでしたが、この公式を使って、もっと多くの数字がある数列の合計を出してみましょう!
類題1(ペア式の練習)
公式「等差数列の合計=(はじめの数+最後の数)✕数の個数÷2」の言葉に数字を入れていきます(代入)
「はじめの数」は1,「数の個数」は100 ですが、「最後の数」つまり100番目の数が書いてありません!
そこで、数列の基本公式「N番目の数」で求めると
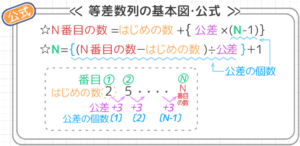
いくつでしょう?
数列は 1,3,5,7,9…なので、はじめの数=1,差=2,N=100 で、100番目の数=1+{2✕(100-1)}=199 ですね
100番目の数が分かったので、和の公式「等差数列の合計=(はじめの数+最後の数)✕数の個数÷2」を使って答を出すと…?
「はじめの数」に1,「最後の数」=100番目の数に今求めた199、「数字の個数」に100 をいれて計算すると、(1+199)✕100÷2=10000です。10000
以上のペア式で、等差数列の合計(和)を出す問題は解けますが、ペア式は、数が奇数個の場合に直感的な理解が難しいので、異なる説明も紹介します。
逆向きの列を足す「逆二段式」
これは数字好きな生徒さん向きかもしれないので、ペア式で十分という人は三番目の「面積式」へ飛んで下さい。
まず、数列の合計を書き出して(図1)、
![]()
同じ数列を最後から並べたものをもとの数列の下に置きます(図2)
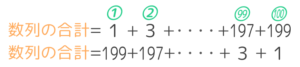
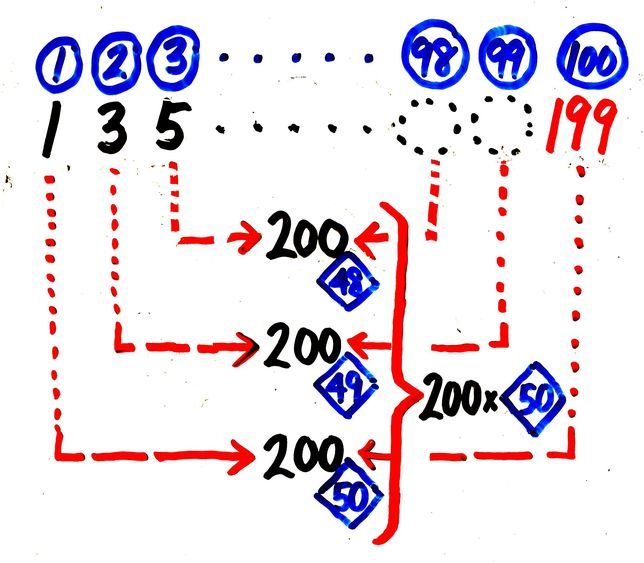
ここで、足し算の筆算のように段の上下の数字を足します(図3)。
すると「=」の右側は「1(はじめの数)+199(最後の数)」と等しい200が100個(数の個数)並ぶので、右側の合計は 200✕100=20000になります。
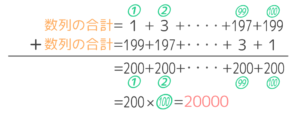
200✕100=20000
一方、「=」の左側は 合計+合計で合計2個分になるので、全体としては、合計2個分=20000となります。
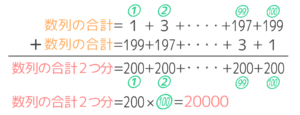
したがって、合計=20000÷2=10000 と分かります。
このように、逆二段式でもペア式と同じく「(初めの数+最後の数)×数の個数÷2」で合計が求められるのです。
階段を組み合わせる「面積式」
三番目の説明は、図形を使った説明です(個人的にはコレが好きです)
スペースの都合上、例題の数列を「 1,3,5,7,9,11,13,15,17,19 」で説明をします。
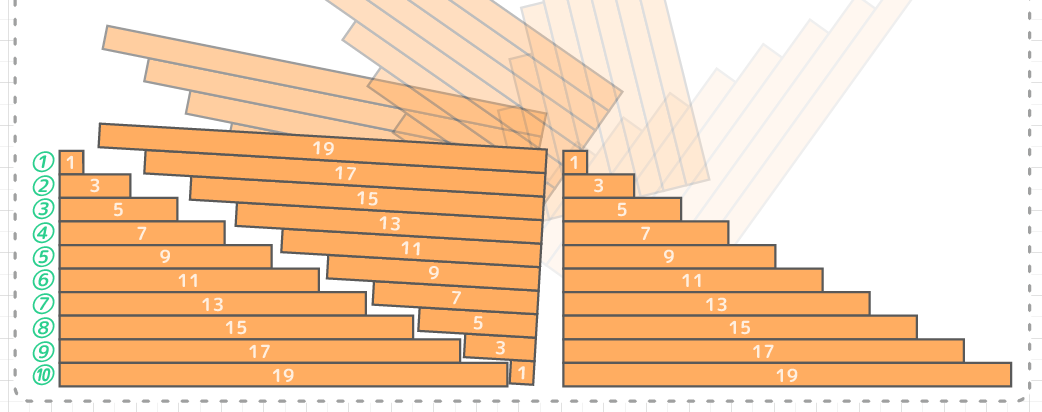
この数列の様子を棒グラフを横倒したように表現すると階段のような形ができて、この面積が数列の合計になります(図1)。
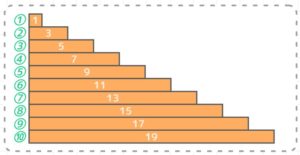
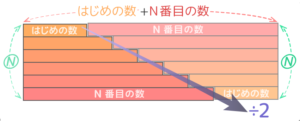
ここで、同じ形をもう一つ作り、逆さまにひっくり返してもとの形と組み合わせると、長方形になります。(図2)
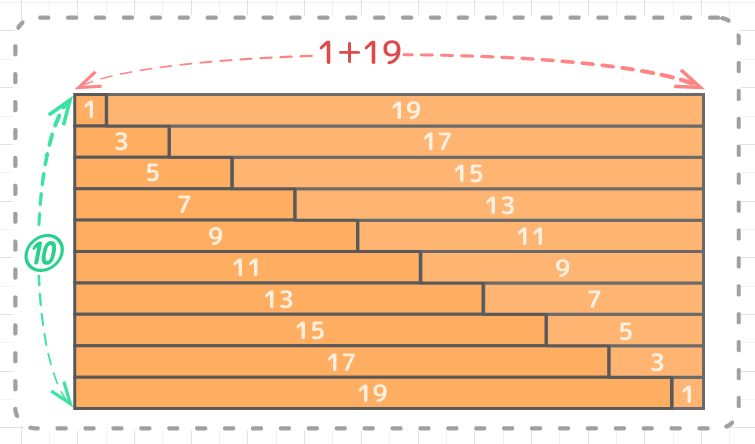
この長方形はタテが10(数の個数)になり、ヨコは1(初めの数)+19(最後の数)で20になるので(図3)、面積は20×10=200になります。(図3)
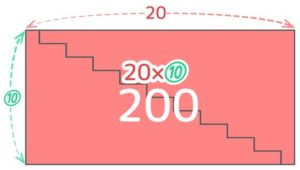
そしてこれは階段の形2個分なので、階段1つ分すなわち数列の合計は 200÷2=100 と分かります(図4)
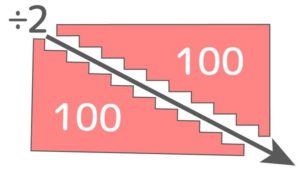
今行った計算は「(1+19)×10÷2」でこれは「(初めの数+最後の数)×数の個数÷2」です。
ペア式・逆二段式と同じ式「(初めの数+最後の数)×数の個数÷2」で合計を求めているのが分かります。
(実は、台形の面積の求め方と全く同じ考え方を使っています)
和の公式が完成♪
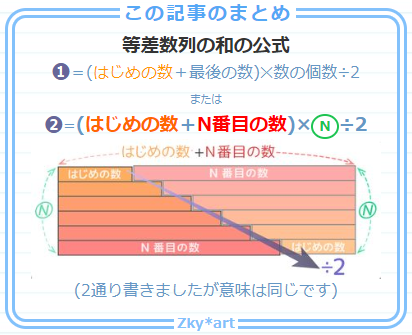
上の3つのどの説明でも、数列の和は「(はじめの数+最後の数)×数の個数÷2」で求められますが、覚えやすくするために今まで出てきた数列の公式と共通の言葉にそろえましょう!
「最後の数」は「N番目の数」、「数の個数」は「N」でしたね!
こうして数列の和の公式「等差数列の和=(はじめの数+N番目の数)×N÷2」が完成しました!ワ~~~~パチパチパチ
等差数列の和=(はじめの数+N番目の数)×N÷2
(問題を解く手順)
- はじめの数、公差、N(合計を求める個数)を確認
- N番目の数を はじめの数+{公差×(N-1)} で求める
- 数列の和を (はじめの数+N番目の数)×N÷2 で求める
 爽茶
爽茶数列の和の問題を解く
 爽茶
爽茶基本解法
もう一度確認すると、こうです。
等差数列の和=(はじめの数+N番目の数)×N÷2
(問題を解く手順)
- はじめの数、公差、N(合計を求める個数)を確認
- N番目の数を はじめの数+{公差×(N-1)} で求める
- 数列の和を (はじめの数+N番目の数)×N÷2 で求める
では確認に1問解いて下さい
2-1:等差数列の和
ヒント
❶はじめの数・公差・Nを確認→❷N番目の数を求める→❸N番目までの和を求める の手順で解きましょう
解説
❶はじめの数・公差・Nを確認
はじめの数=8、公差=3、N=50 ですね。
❷N番目の数を求める
N番目の数=はじめの数+{公差×(N-1)} なので、50番目の数=8+{3×(50-1)}=8+(3×49)=155です。
❸N番目までの和を求める
N番目までの和=(はじめの数+N番目の数)×N÷2 なので、50番目までの和=(はじめの数+50番目の数)×50÷2=(8+155)×50÷2=163×50÷2=4075 です
実は、最後の計算(163×50÷2=4075)にはコツがあります。
●数列の和の公式の「はじめの数+N番目の数」と「N」のどちらかは必ず偶数になるので、最初にかけ算ではなく「偶数になった数」÷2を暗算で出してしまうと計算が楽になります。
○上の例題では 163×50÷2 なので 50÷2=25 を暗算して、163×25 を筆算します
○もし、49番目までの和なら、152×49÷2 という式になるので、最初に152÷2=76を暗算して、76×49を筆算します。
練習問題をどうぞ
2-1:等差数列の和
解説
❶はじめの数は5、公差は4、Nは45です。
❷N(45)番目の数=5+{4×(45-1)}=181 になります。
❸等差数列の和=(はじめの数+N番目の数)×N÷2 の公式を使います。
45番目までの和=(5+181)×45÷2=186×45÷2=186÷2×45=93×45=4185と分かります。
ヒント
公式を使うには「169」が何番目か求める必要がある
解説
❶はじめの数は5、公差は4ですが、Nが分かりません。
その代わり、N番目の数=169 と分かるので、ここからNを求めます。

上のような公式か、「169=5+{4×(N-1)}」を逆算してNを求めると、N=42です。
❷N番目の数は169 と分かっていました。
❸42番目までの和=(5+169)×42÷2=174×42÷2=174÷2×42=87×42=3654と分かります
計算を楽にするコツはありますが、最後は筆算をしなくてはいけないので、計算力をつけておきましょう。
●数列の和の問題は計算が面倒くさいので、
計算力をつけておくのも大切です
次は少し応用した問題を解いてみましょう。
プチ応用
3-1:等差数列の和
解説
❶「はじめの数」は3、「公差」は5、「N」は9
❷N(9)番目の数は 3+{5×(9-1)}=43
❸はじめから9番目までの和は (3+43)×9÷2=207 と分かります。
ヒント
10番目の数が「はじめ」で、30番目の数が「終わり」になるような新しい数列を作ってみる
解説
10番目の数と30番目の数がはじめと終わりになるような新しい数列を作ってみます。
10番目の数は、先程出した9番目の数「43」+公差5なので48、30番目の数は、3+{5×(30-1)}=148 です。
30番目の数は10番目の数からは 30-10+1=21番目の数になります。(最後の「+1」は「番目=番差+1」なので。番目(木)と番差(間)の関係については過去の記事「番号付き植木算」を参照して下さい)
したがって「10番目の数から30番目の数までの和」というのは「48,…,148 という21個の等差数列の和」と等しくなります。
はじめの数=48、N番目の数=148、N=21なので、和の公式を作ると、(48+148)×21÷2=2058になります。
別解
もう一つの解き方も書いておきます。一度理解すればこちらの方が簡単なので、算数が苦手な人にはコチラがオススメです。
「10番目の数から30番目の数までの和」というのは、「はじめから30番目までの和」-「はじめから9番目の和(10番で無いことに注意)」と等しくなります。
はじめから30番までの和=(5+148)×30÷2=2265、はじめから9番までの和=小問1で求めた207 なので
10番から30番までの和=2265-207=2058 と分かります
解説
❶はじめの数=3、公差=5、123が何番目か(N)が分からないので、N={(N番目の数-はじめの数)÷公差}+1 から N={(123-3)÷5}+1=25
❷N番目の数は123と分かっています。
❸和の公式=(はじめの数+N番目の数)×N÷2 を使って (3+123)×25÷2=1575 と分かります
ヒント
小問(2)と同じように考えて…
解説
小問(2)のように、「53」から「123」までの新しい数列を作ります。
「53」は小問2で出した10番目の「48」の次なので11番目と分かります。
「123」は小問3で25番目だったので、11番目の「48」から数えると、25-11+1=15番目と分かります。
つまり「53」から「123」までの和は「53,…,123という15個の等差数列の和」と等しいことになります。
和の公式を使って、(53+123)×15÷2=1320 と分かります
分かりましたね?
もっと問題を解きたい人はこの下にある「オススメ教材」のコーナーを見て下さい
まとめとプリント
数列の和の公式をもう一度示します。数字だけでなく必ず日本語で「記憶」してください。
等差数列の和=(はじめの数+N番目の数)×N÷2

(問題を解く手順)
- はじめの数、公差、N(合計を求める個数)を確認
- N番目の数を はじめの数+{公差×(N-1)} で求める
- 数列の和を (はじめの数+N番目の数)×N÷2 で求める
この記事で使った問題の「解答解説」プリントをダウンロードできます。書き込み可能な「問題」プリントはコチラでまとめてダウンロードできます。
 爽茶
爽茶おすすめ教材
 爽茶
爽茶もっと問題を解きたい人にオススメ教材を紹介♪
分かりやすい!と評判のスタディサプリにも「数列」の動画授業がありますよ。今なら14日間無料
興味がある人は「先取りや予習・復習に! スタディサプリ そうちゃ式のオススメ利用法」へ
●数列だけを解きたい場合、低学年の入門用には「等差数列(上)」
●数列だけでなく算数全体の復習をしたい場合、小4受験生には「算数の基本問題4年」(日能研)
2023年度生徒さん募集
2023年度の生徒さんの募集を開始しました(対面授業の一次募集)
東武野田線・伊勢崎線沿線にお住まいの新5年生で予習シリーズをベースにされている方が対象です。
詳しくはコチラのページを御覧下さい
新4年生の方を対象に学習相談/授業を実施します(サピックス新越谷校・南浦和校・大宮校の方が対象。締め切り2/1)。応募はコチラから
中学受験でお悩みの方へ
 そうちゃ
そうちゃ受験に関する悩みはつきませんね。「中学受験と高校受験とどちらがいいの?」「塾の選び方は?」「途中から塾に入っても大丈夫?」「塾の成績・クラスが下がった…」「志望校の過去問が出来ない…」など
様々なお悩みへのアドバイスを記事にまとめたので参考にして下さい。
自分だけで悩んでいると煮詰まってしまい、事態を改善できないかもしないこともあるでしょう…
そんな時は、講師経験20年の「そうちゃ」に相談してみませんか?対面/オンラインの授業/学習相談を受け付けているので、ご利用下さい。
この記事があなたの役に立てたなら嬉しいです!