等差数列の基本をガチガチに固めたい!」という中学受験生の方、まかせて下さい♪
東大卒講師歴20年の管理人が「はじめの数」や「公差」の求め方を分かりやすく図解します。
ライバルに差をつけられますよ!
目次をクリックすると、好きなところにジャンプできます。
等差数列の基本(復習)
等差数列の基本図を見ると4つの要素があるのが分かります。
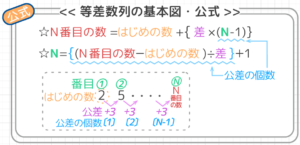
①「はじめの数」
②「公差」
③「N」(「番目」)
④「N番目の数」
④「N番目の数」③「N」が基礎なので、確認テストをどうぞ。(出来なかった人は「数列の総合案内」から復習すると良いですね!)
「1,7,13…」という等差数列がある時、15番目の数は?
→N番目の数=はじめの数+{公差×(N-1)}
→( 1+6×(15-1)=85 )
127は何番目か?
→N={(N番目の数-はじめの数)÷差}+1
→( {(127-1)÷6}+1=22番目 )
今回は、残りの①「はじめの数」②「公差」を求めます。
等差数列の「差」を求める
解き方を理解♪
1-1:公差を求める
ヒント
32が何番目か、はじめの数からいくつ増えているかを考えます。
(解答)
32は「はじめの数」4から32-4=28増えています。
そして32は5番目の数で「はじめの数」に公差を5-1=4回足したものです。
つまり公差を4回加えたら28増えたということです
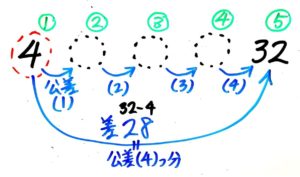
公差4回分が28なので、公差1つは28÷4=7と分かります。
公式にしてみる
例題を解く時に使った計算を公式の形にすると、こうなります。
=(N番目の数-はじめの数)÷(Nー1)
*(Nー1)が公差の個数になっている。
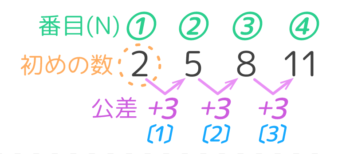
(例)等差数列「4,◯,◯,◯,32…」の公差?
→5番目の数が32,はじめの数なので、(32-4)÷(5-1)=7
ですが、この公式自体を暗記しなくても問題がとければOKです!
類題で定着!
1-2:公差を求める
解説
はじめの数と20番目の数の差は95
20番目の数まで公差は20-1=19個あります。
(植木算の「間=木-1」ですね)
よって、公差19個分が95にあたると分かります。
公差1つは95÷19=5 ですね
解説
公差が分かったので、N番目の数を求める公式が使えます。
N番目の数=初めの数+{公差×(N-1)}
これに、初めの数=13,公差=5,N=1000を入れてみると
13+5×(1000-1)=5008 と分かります。
これで「公差」の出し方は大丈夫ですね?
「はじめの数」の求め方
等差数列の基本の最後は「はじめの数」を求める問題です。
解き方を理解
誘導に従って解いて下さい
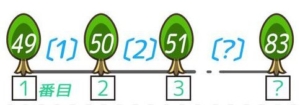
2-1:はじめの数を求める
解説
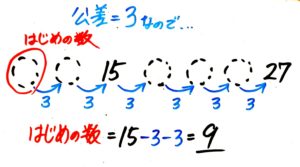
分かっている数「15」「27」に注目すると、15から27までは12増加しています。、
そして「27」と「15」の間の公差は4個なので、公差4個=12と分かります。
したがって、公差1個は12÷4=3と分かります。
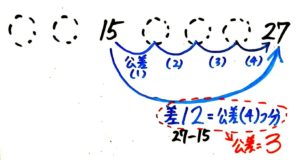
解説
15と「はじめの数」の間の公差は=2個で、公差2個分は3✕2=6になります。
よって「はじめの数」=15-6=9と分かります。
公式にしてみる
今行った計算を公式にすると、こうなります。
=N番目の数-{公差×(Nー1)}
*(Nー1)が公差の個数になっている

(例)等差数列「○,○,26,○,42」の「はじめの数」は?
→公差は(42-26)÷2=8
→はじめの数は26-{8×(3-1)}=10
ですが、この公式も無理に暗記せずとも問題が解ければOKです。
2-2:はじめの数を求める
図解
「番号の付いた植木算」を思い出すと良いです。
14番目と21番目の差は164-108=56です。これが公差何個分にあたるのか考えます。
14番目と21番目の間に公差がいくつあるのかは、番号付き植木算を思い出すと簡単です。
番号の差が21-14=7なので公差も7個です。
つまり差56=公差7個分です。
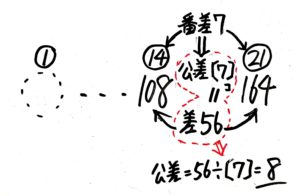
よって公差一つは56÷7=8 とわかります。
図解
はじめの(1番目の)数と14番目の数の間の公差の数は14-1=13個です。
そして、さっき公差が8と出たので「はじめの(1番目の)数」と14番目の数の差は13×8=104です。
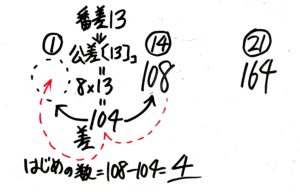
よって、はじめの数は108-104=4 と分かります。
まとめとプリント
差と初めの数の求め方をもう一度見てみましょう。
=(N番目の数-はじめの数)÷(Nー1)
*(Nー1)が公差の個数になっている。

(例)等差数列「4,◯,◯,◯,32…」の公差?
→5番目の数が32,はじめの数なので、(32-4)÷(5-1)=7
=N番目の数-{公差×(Nー1)}
*(Nー1)が公差の個数になっている

(例)等差数列「○,○,26,○,42」の「はじめの数」は?
→公差は(42-26)÷2=8
→はじめの数は26-{8×(3-1)}=10
これらは暗記するというよりも式を作ることができればOKです。
この記事で使った問題の「解答解説」プリントをダウンロードできます。書き込み可能な「問題」プリントはコチラでまとめてダウンロードできます。
 爽茶
爽茶他の数列の記事も「数列の総合案内」から見て下さい。
●数列だけを解きたい場合、低学年の入門用には「等差数列(上)」
●数列だけでなく算数全体の復習をしたい場合、小4受験生には「算数の基本問題4年」(日能研)
2023年度生徒さん募集
2023年度の生徒さんの募集を開始しました(対面授業の一次募集)
東武野田線・伊勢崎線沿線にお住まいの新5年生で予習シリーズをベースにされている方が対象です。
詳しくはコチラのページを御覧下さい
新4年生の方を対象に学習相談/授業を実施します(サピックス新越谷校・南浦和校・大宮校の方が対象。締め切り2/1)。応募はコチラから
中学受験でお悩みの方へ
 そうちゃ
そうちゃ受験に関する悩みはつきませんね。「中学受験と高校受験とどちらがいいの?」「塾の選び方は?」「途中から塾に入っても大丈夫?」「塾の成績・クラスが下がった…」「志望校の過去問が出来ない…」など
様々なお悩みへのアドバイスを記事にまとめたので参考にして下さい。
自分だけで悩んでいると煮詰まってしまい、事態を改善できないかもしないこともあるでしょう…
そんな時は、講師経験20年の「そうちゃ」に相談してみませんか?対面/オンラインの授業/学習相談を受け付けているので、ご利用下さい。
この記事があなたの役に立てたなら嬉しいです!


