「難関校の入試問題を解けるようになりたい!」という中学受験生の方へ。等差数列の応用問題を東大卒講師歴20年の図解講師「そうちゃ」が分かりやすくまとめました♪この記事の問題が解ければ入試問題にも刃が立つようになるでしょう!
数列の基本事項(復習)
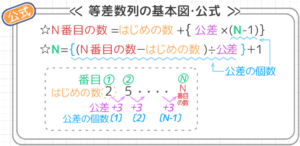
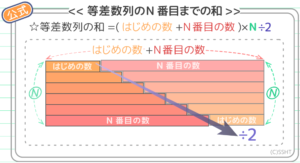
過去の記事の要点です。最低限、これらを頭に入れて下さい。
この図が「?」な人は「N番目の数の出し方」「Nの出し方」「等差数列の和」を身につけてからチャレンジして下さい。
分数の数列(○○なし)
 爽茶
爽茶考え方を理解♪
●例題1-(1)
分子と分母はそれぞれどのような数列になっているか
下の表を埋めるつもりで考えてみましょう
| 番号 | 1 | 2 | 3 | 4 | 5 |
| 分子 | |||||
| 分母 |
分子と分母を2列の表にしてみると、規則性が分かります。
| 番号 | 1 | 2 | 3 | 4 | 5 |
| 分子 | 2 | 5 | 8 | 11 | 14 |
| 分母 | 3 | 7 | 11 | 15 | 19 |
分子:はじめの数2,公差3の等差数列
分母:はじめの数3,公差4の等差数列
このように分数の数列が出てきたら、まずは分母と分子を二列の表にすると考えやすくなります。
そして分子と分母の規則性が分かったら、右端に「N番目の数」を書き込んでおくと良いです。
| 番号 | 1 | 2 | 3 | … | N |
| 分子 | 2 | 5 | 8 | … | 2+{3×(N-1)} |
| 分母 | 3 | 7 | 11 | … | 3+{4×(N-1)} |
ここから先は、この表を使っていきましょう。
●例題1-(2)
10番目の分数を求めよ
さきほどの「実戦的な表」を使いましょう
先程の表を使って10番目の分子(上段)を計算すると、等差数列のN番目の数の公式「N番目の数=はじめの数+公差×(N-1)」を使って 2+{3×(10-1)}=29です。
同様に10番目の分母(下段)を計算すると、3+{4×(10-1)}=39なので…
| 番号 | 1 | 2 | 3 | … | 10 |
| 分子 | 2 | 5 | 8 | … | 2+{3×(10-1)} |
| 分母 | 3 | 7 | 11 | … | 3+{4×(10-1)} |
10番目の分数は2939です。2939
●例題1-(3)
6283は何番目の分数か
分子と分母のどちらを使ってもかまいません。
分子を使って解いてみます。分子が62なので、表の上の段の何番目が62になるか(N)を求めます。
| 番号 | 1 | 2 | 3 | … | N |
| 分子 | 2 | 5 | 8 | … | 29 |
| 分母 | 3 | 7 | 11 | … | 39 |
等差数列の「N」を求める公式「N={(N番目の数-はじめの数)÷公差}+1」 を使うと、?={(62-2)÷3}+1=21 です。
6283は21番目です。21番目
●例題1-(4)
何番目かの分数が○67になった。◯を求めよ。
(3)と違って分母しか分からないので、分母を使いましょう
まず分母が67になるのが何番目か(N)を求めます
| 番号 | 1 | 2 | 3 | … | N |
| 分子 | 2 | 5 | 8 | … | ○ |
| 分母 | 3 | 7 | 11 | … | 67 |
公式「N={(N番目の数-はじめの数)÷公差}+1」を使って、N={(67-3)÷4}+1=17番目です。
次に分子の17番目(表の◯)を、等差数列のN番目を求める公式で求めると、◯=2+{3×(17-1)}=50です。
| 番号 | 1 | 2 | 3 | … | 17 |
| 分子 | 2 | 5 | 8 | … | 2+{3×(17-1)} |
| 分母 | 3 | 7 | 11 | … | 67 |
以上より「ある分数」は5067で、◯は50です。50
●例題1-(5)
分子と分母の差が33になるのは何番目か

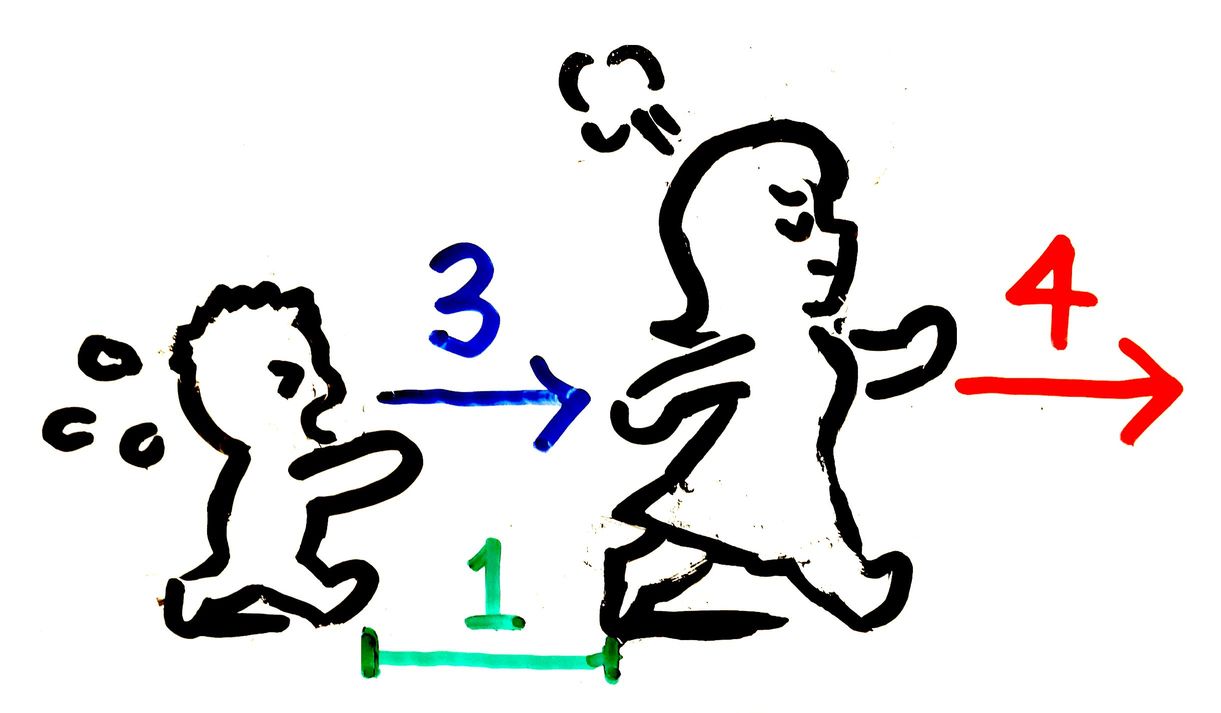
母と子の距離が開いていきます
この問題の場合は、一番目の差が1、二番目の差が2…と広がっていくので…差が33になるのは33番目と直感で分かります。33番目
ただ…他の問題にも対応できるようにしたいので、こういう問題は「旅人算」のつもりで観察するとおぼえておきましょう。
この問題の場合は、最初の分子と分母の差は1で、分子が3ずつ分母が4ずつ増えていくので、差は4-3=1 ずつ、どんどん開いていきます。
子供の「うえ~ん」という声が聞こえてきそう…
この差が33になるのは、あと32差がつかないといけないので、32÷(4-3)=32番後で、1番目の32番後なので、1+32=33番目 と計算します。
番目と番後について詳しく知りたい人は参考記事「番号付き植木算」を見て下さい。
解き方がわかったところで、類題を解いてみましょう!
練習して定着!
類題1(分数の数列)
 爽茶
爽茶次は◯◯有りの問題です!
分数の数列(○○あり)
 爽茶
爽茶これは普通の数字ではできないが分数では出来る何かです。これが解答のポイントでもあります。一体何でしょうか?
考え方を理解♪
●例題2-(1)
とりあえず表を作りましょう…ね
とりあえず、先程と同じように分子と分母を2列の表にしてみます。
| 番号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | … | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 分子 | 5 | 7 | 3 | 11 | 13 | 5 | 17 | … | |||
| 分母 | 6 | 9 | 4 | 15 | 18 | 7 | 24 | … | |||
分子を見ると「5,7,3,11,13…」となっていて、3と5の周辺が等差になりません!3が9,5が15だったら良いのに…
(>_<)
分母も4と7の周辺が等差になりません!4が12、7が21だったら良いのに…
(>_<)
ところが、よく見ると…分子も分母も両方とも、3番目と6番目がおかしいですね。
Σ(゚◇゚;)!!
「約分してあったんだ!」と気付きます
34を912に、57を1521に直すと、表はこうなります。
| 番号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | … | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 分子 | 5 | 7 | 9(3) | 11 | 13 | 15(5) | 17 | … | |||
| 分母 | 6 | 9 | 12(4) | 15 | 18 | 21(7) | 24 | … | |||
これで、答えられますね。
分子:はじめの数5,公差2の等差数列
分母:はじめの数6,公差3の等差数列
このように、分数の数列は約分されている可能性を頭に入れておく必要があります。
タイトルの〇〇は「約分」だったのですね
(*^ー゚)b
ここからは、約分されていないかも考えて下さい!
●例題2-(2)
表を使えば簡単ですね
12番目の分子(上段)を計算すると 5+{2×(12-1)}=27で、12番目の分母(下段)を計算すると、6+{3×(12-1)}=39 になります。
| 番号 | 1 | 2 | 3 | 4 | 5 | … | 12 | … | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 分子 | 5 | 7 | 9(3) | 11 | 13 | … | 27 | … | |||
| 分母 | 6 | 9 | 12(4) | 15 | 18 | … | 39 | … | |||
以上より、12番目の数は2739ですが約分をして913と答えないといけません。913
●例題2-(3)
2つの場合を考える必要があります!
分子が35なので表の上の段の何番目が35になるか(N)を求めたくなります。しかし、この問題では約分があるので…「35」が約分した数字で,元々は35×3=105 であった可能性があるのです。
すなわち、2つの場合が考えられるということです。
●場合その1(35は約分していない数字)
| 番号 | 1 | 2 | 3 | 4 | 5 | … | ? | … | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 分子 | 5 | 7 | 9(3) | 11 | 13 | … | 35 | … | |||
| 分母 | 6 | 9 | 12(4) | 15 | 18 | … | 51 | … | |||
●場合その2(35は約分した結果)
| 番号 | 1 | 2 | 3 | 4 | 5 | … | … | ? | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 分子 | 5 | 7 | 9(3) | 11 | 13 | … | … | 105(35) | |||
| 分母 | 6 | 9 | 12(4) | 15 | 18 | … | … | 153(51) | |||
このように2つの場合があって、しかもどちらの場合が正しいのかパッと分からない時は、易しい方から確かめていきましょう。
今回は「35」は約分していない数字だとして、つまり場合1として計算します。
すると…N={(35-5)÷2}+1=16 です。
次に、分母の16番目が約分せずに51になるか確認をします。 6+{3×(16-1)}=51 になりました(ホッ)
これで、自信を持って3551は16番目と答えられますね。16番目
●例題2-(4)
ここの問題も2つの場合を考える必要があります
40になりません(泣)
| 番号 | 1 | 2 | 3 | 4 | 5 | … | … | 12 | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 分子 | 5 | 7 | 9(3) | 11 | 13 | … | … | 27 | |||
| 分母 | 6 | 9 | 12(4) | 15 | 18 | … | … | 39 | |||
つまり、分子の「27」は約分した数字で分子の元々の数字は27×3=「81」だったんですね
| 番号 | 1 | 2 | 3 | 4 | 5 | … | … | ? | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 分子 | 5 | 7 | 9(3) | 11 | 13 | … | … | 81(27) | |||
| 分母 | 6 | 9 | 12(4) | 15 | 18 | … | … | ||||
気を取り直して…分子が81になるのは何番目か計算すると N={(81-5)÷2}+1=39 です。
次に、分母の39番目が40×3=「120」になるか確認すると…6+{3×(39-1)}=120 良かった。OKです。
| 番号 | 1 | 2 | 3 | 4 | 5 | … | … | 39 | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 分子 | 5 | 7 | 9(3) | 11 | 13 | … | … | 81(27) | |||
| 分母 | 6 | 9 | 12(4) | 15 | 18 | … | … | 120(40) | |||
これで自信を持って2740(約分する前は81120)は39番目といえますね。39番目
ちょっと面倒くさかったかもしれませんね。
物足りない人は、類題で練習しましょう
練習して定着!
類題2
まとめ
分数の数列では、約分に気を付けつつ、分子と分母を二段の表に整理すると解きやすくなります。
 爽茶
爽茶他の数列の記事も「数列の総合案内」から見て下さい。
追記(2020.3.9)
一年以上ぶりに記事を見返してみたらレイアウトがひどすぎたのでリデコ
この記事を最初に書いたのはブログを始めて1ヶ月目くらいの頃で、表や分数・丸数字の表現に悪戦苦闘していたのを思い出しました。
2023年度生徒さん募集
2023年度の生徒さんの募集を開始しました(対面授業の一次募集)
東武野田線・伊勢崎線沿線にお住まいの新5年生で予習シリーズをベースにされている方が対象です。
詳しくはコチラのページを御覧下さい
新4年生の方を対象に学習相談/授業を実施します(サピックス新越谷校・南浦和校・大宮校の方が対象。締め切り2/1)。応募はコチラから
中学受験でお悩みの方へ
 そうちゃ
そうちゃ受験に関する悩みはつきませんね。「中学受験と高校受験とどちらがいいの?」「塾の選び方は?」「途中から塾に入っても大丈夫?」「塾の成績・クラスが下がった…」「志望校の過去問が出来ない…」など
様々なお悩みへのアドバイスを記事にまとめたので参考にして下さい。
自分だけで悩んでいると煮詰まってしまい、事態を改善できないかもしないこともあるでしょう…
そんな時は、講師経験20年の「そうちゃ」に相談してみませんか?対面/オンラインの授業/学習相談を受け付けているので、ご利用下さい。
この記事があなたの役に立てたなら嬉しいです!