「等差数列の基本を固めたい」という中学受験生の方、まかせて下さい。東大卒講師歴20年の図解講師「そうちゃ」が「ある数の等差数列上での位置=N」の出し方を分かりやすく説明します。
等差数列の基礎(復習)
 爽茶
爽茶こんにちは!「そうちゃ」@zky_tutor(プロフィール)です。
まず等差数列の基礎を確認します。
こうでしたね。
確認テストをどうぞ
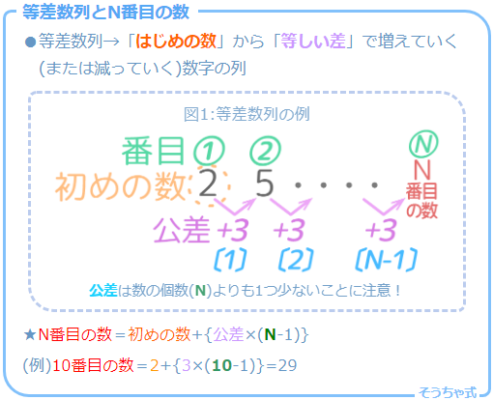
等差数列 3,10,17,24…の13番目の数を求めなさい
→( はじめの数は3、公差は7、Nは13 なので
13番目の数=3+{7×(13-1)}=3+84=87 )
確認テストができない人は「等差数列の基本とN番目の数」を見た方が良いかもしれません。
できた人は今日の内容に進みましょう♪
Nを求める
 爽茶
爽茶解き方を理解♪
●例題1
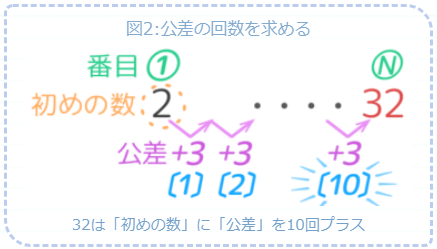
等差数列 2,5,8,11…がある。32が何番目の数か考える。
「はじめの数」と「公差」を使って考えます。
例題1(1)
32は はじめの数2に+30した数です。

30
例題1(2)
+30は公差3の10回分(30÷3)にあたります。
10回分
例題1(3)
等差数列では、数が公差より一つ多くなります(植木算の木と間の関係)。
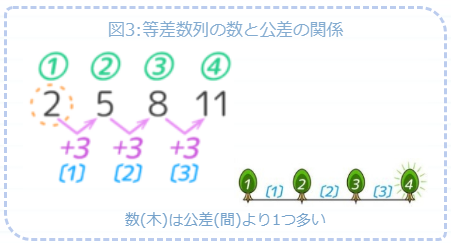
今回の問題では、公差が10回なので数は11個になります。つまりN=11で32は11番目の数です♪
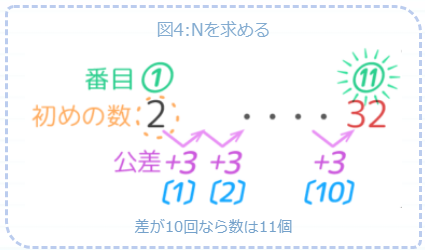
11番目
解き方を公式化
今の計算を振り返ると、こうでした。

これから先は何回もNを求めるので、この計算自体を公式としておきましょう!
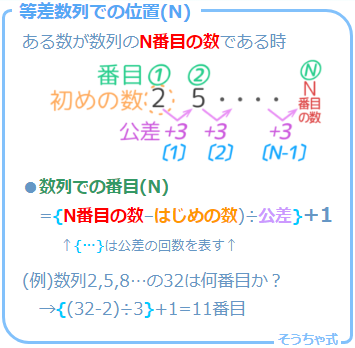
中括弧{…}の部分が公差の回数になっているのが分かります。
これで等差数列の「N」の求め方は分かりました。類題で公式を使う練習をしましょう
練習問題で定着!
●類題1-1
9,15,21…という等差数列があります。以下の問いに答えなさい。
類題1(1)
公式を使いましょう。
公式「N={N番目の数–はじめの数)÷公差}+1」にN番目の数=75,はじめの数=9,公差=6を代入すると、N={75–9)÷6}+1={11}+1=12番目と分かりますね!
12番目
類題1(2)
ありますか?と聞かれているということは…
N番目の数=100,はじめの数=9,公差=6を代入すると公式に入れて計算するとN={(100-9)÷6}+1=16.1…で、Nが整数になりません。
つまり、100は数列上にはありません。
N=16.1…ということは、100は16番目と17番目の間にあるということです。
ない。16番と17番の間
類題1(3)
小問(2)がヒントになっています
N番目の数を1000にして公式を使うと、N={(1000-9)÷6}+1=166.1…で1000は数列上になく、166番目と167番目の間にあると分かります。
したがって1000を越えるのは167番目の数ですね!
167番目
●類題1-2
12,16,20…という等差数列が76まで続いています。以下の問いに答えなさい。
類題1-2(1)
深く考えずに…
N番目の数=76,はじめの数=12,公差=4を公式に代入すると、N={(76-12)÷4}+1=16+1=17なので、最後の数76は17番目とわかります。
17個
類題1-2(2)
真ん中のものは「(1+全部の数)÷2」番目です。
全部17個並んでいるので、真ん中の数字は(1+17)÷2=9番目です。
前回の公式「N番目の数=初めの数+{公差×(N-1)}」にはじめの数=12,公差=4,N=9を代入して計算すると12+{4×(9-1)}=44です。
44
等差数列では、真ん中の数は「初めの数+最後の数)÷2」でも求められます。(12+76)÷2でやはり44になります。
類題1-2(3)
全部で10個ある時の前から4番目の数は、後ろから数えると10-(4-1)=7番目です。
40が(前から)何番目か求めると、N={(40-12)÷4}+1=8番目です。つまり「40」の前には数字が8-1=7個あります。
この数列は全部で17個の数字があるので、後ろから数えると「40」は17-7=10番目になります。(詳しくは参考記事「数え方」を見て下さい)
10番目
後ろからの番目を聞かれているので、数列を前後逆向きにして、初めの数=76,最後の数=12と考えます。公差は4で変わりません(減っていきます)。
Nを求める公式「N={}+1」に代入すると、N={(76-40)÷4}+1=10番目と分かります。
(毎日更新)AI問題に挑戦
(作成中です)
まとめとプリント
まとめ
今回の公式「Nを求める」と前回の公式「N番目を求める」、それに等差数列の基本図をまとめてみました。

公式に直接書いていない「公差の個数(青い波線)」がポイントです。
この記事で使った問題の「解答解説」プリントをダウンロードできます。書き込み可能な「問題」プリントはコチラでまとめてダウンロードできます。
 爽茶
爽茶他の数列の記事は「数列の総合案内」から見て下さい
●数列だけを解きたい場合、低学年の入門用には「等差数列(上)」
●数列だけでなく算数全体の復習をしたい場合、小4受験生には「算数の基本問題4年」(日能研)
2023年度生徒さん募集
2023年度の生徒さんの募集を開始しました(対面授業の一次募集)
東武野田線・伊勢崎線沿線にお住まいの新5年生で予習シリーズをベースにされている方が対象です。
詳しくはコチラのページを御覧下さい
新4年生の方を対象に学習相談/授業を実施します(サピックス新越谷校・南浦和校・大宮校の方が対象。締め切り2/1)。応募はコチラから
中学受験でお悩みの方へ
 そうちゃ
そうちゃ受験に関する悩みはつきませんね。「中学受験と高校受験とどちらがいいの?」「塾の選び方は?」「途中から塾に入っても大丈夫?」「塾の成績・クラスが下がった…」「志望校の過去問が出来ない…」など
様々なお悩みへのアドバイスを記事にまとめたので参考にして下さい。
自分だけで悩んでいると煮詰まってしまい、事態を改善できないかもしないこともあるでしょう…
そんな時は、講師経験20年の「そうちゃ」に相談してみませんか?対面/オンラインの授業/学習相談を受け付けているので、ご利用下さい。
この記事があなたの役に立てたなら嬉しいです!


