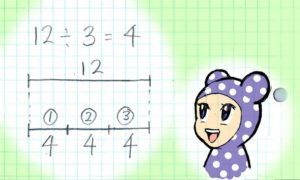文章問題が苦手!どうすれば良いの?」とお悩みの方へ
文章題でおかしな式を作ったりする場合は、数量の感覚がイメージとして身についていないことが多いです。
そこで東大卒講師歴20年の図解講師「そうちゃ」が数量感覚のイメージを養う勉強法を紹介します。
この記事を読んで真似すれば、文章題でおかしな式を作ることは少なくなっていくでしょう!
文章題が苦手!
数の感覚が弱い?
小学校中学年くらいの生徒さんのお母様がこうおっしゃることがあります。
「ウチの子、数字の感覚が弱い」(-_-)
その話を聞いて、生徒さんの様子を見てみると確かに、単純な計算問題はきちんと出来る
(^_^)v
それなのに逆算が出来ない!
(*_*)
文章問題が出来ない!!
(ToT)
こういうことが結構有ります。
これはどういう事かというと、計算の「意味」、つまりどのような関係の数量をどのように操作しているのかそれをイメージできないという事です。
じゃあ、どうすれば?
そういう生徒さんにやってもらうのは、
まず、四則計算を線分図にしてもらうこと(授業では生徒さんにカードを作ってもらいます↓)
それを自主学習で反復しイメージできるようにする(^_^)v
すると、逆算が出来るようになり、文章問題でもおかしな式を書かずに正しく立式できるようになります。
線分図を書く前に…
計算の「意味」
四則計算を線分図にする前に確認すべきことがあります。
それは、四則計算の「意味」を日本語としてきちんと分かっているか?
計算は出来るのに文章問題が出来ない生徒さんに多いのが「こういう記号が出てきたらこういう筆算をすれば良いんでしょ!」という認識
この理解では非常にまずいです
(>_<)
計算の「意味」とは数量をどのように操作するか?ということです。
四則計算の「意味」テスト!
例題の計算の意味は?と聞いて、だいたい同じような日本語が返ってくれば合格です(「足す」「引く」「かける」「割る」という日本語は禁止ですw)
足し算
5+3=8 の意味は?
→「5に3を加えたら(合わせたら)8になった」
引き算
8-3=5 の意味は?
→「8から3を取ったら(消したら)5になった」
かけ算
2×3=6 の意味は?
→「2を3つ集めたら(並べたら)6になった」
6÷3=2 の意味は?
→「6を3等分したら2ずつになった」
特にかけ算、割り算について同じような日本語が返ってこない場合は、何度も練習しましょう。(私の授業では、プリントかカードを作ります)
四則計算の意味を線分図に対応させたシリーズはこちらです。「足し算と引き算の線分図」
(2021/6/26只今準備中です)