「方陣算」を学習している中学受験生の方「石がたくさん並んでいて面倒くさく、難しそう…」と思っていませんか?
実は、ちょっとした図を書くだけで方陣算はずっと簡単に解けるんですよ!
この記事では東大卒講師歴20年の図解講師「そうちゃ」が授業で教えている「区切り図」の書き方を使った基礎から応用問題の解き方を分かりやすく説明します。
記事を読んで真似するだけで方陣算が苦手で無くなるかも!
目次をクリックすると好きな場所にジャンプできます。
方陣算とは
方陣は戦争で兵士が作る正方形/長方形の「陣」形(Wikipediaでの解説)です。
「方陣算」は方陣の人数(個数)を計算する問題です。パズル・ゲームだと思って楽しみましょう!
石を並べる問題は、いくつかに分けて考えると楽に理解できます。「中実方陣」「中空方陣」「三角陣」「多角形並べ」の順に説明していきます
中実方陣
中まで詰まった方陣です。石の数は正方形の面積と同じ式で出せます。
一辺A個の中実方陣→「A×A」個の石を持つ
(例)一辺4個の中実方陣
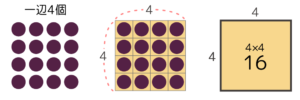
一番右の図が大切です。
最外周の石の個数
一番外側(最外周)に並んだ石の数は4つのグループの合計で出します。
四隅を意識した区切り図を書いて、それをもとに4つのグループに分けます。
一辺A個の中実方陣の最外周の石の数
=(A-1)×4
(例)一辺4個の中実方陣の最外周の石の数
→(4-1)×4=12個
(図の書き方:実体図から区切り図へ)
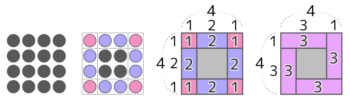
左から3番目の「井」のような区切り図を書くのが方陣算を解く一番のコツです!
確認テストをどうぞ
一辺10個の中実方陣の最外周の石の数は?
→( (10-1)×4=36個 )
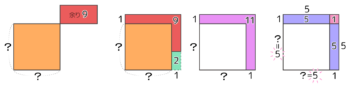
タテヨコ一列増やす
基本
ここでも「区切り図」を書けるようにしておく。
一辺A個の中実方陣を縦横一列増やすのに必要な石の数
→(A×2)+1 個の石が必要
(例)一辺4個の場合の区切り図
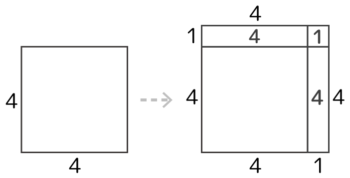
(4×2)+1=9個の石が必要と分かる
応用(余った石で一列増やそうとすると不足)
区切り図を書いて考えてます。
くわしく見たい、問題を解きたい人は「中実方陣」を見て下さい。
長方形の中実方陣
考え方は正方形の場合と同じです。
●石の総数→A×B
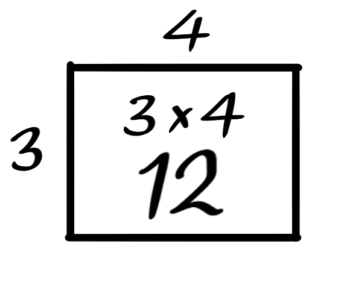
●最外周の石の数→{(A-1)+(B-1)}×2
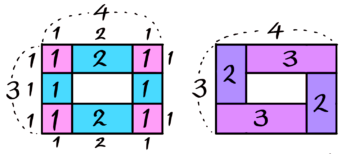
●縦横一列ふやすのに必要な石の数
→(A+B)+1個
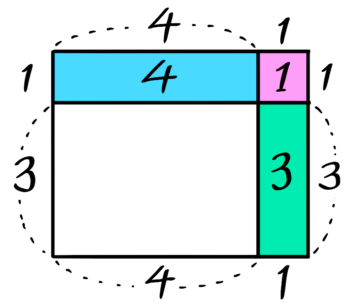
くわしい説明を読みたい「余ったので縦横一列増やそうとしたら足りない」等の問題を解きたい人は「中実方陣」を見て下さい。
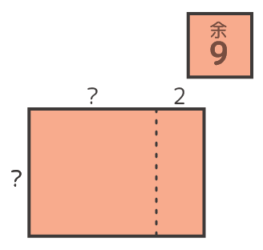
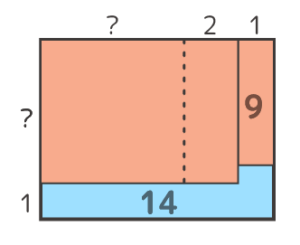
石が9個余ったので
一列増やそうとしたら
14個足りない
中実方陣をじっくり学習したい人は参考記事「中実方陣」を見て下さい。
中空方陣
中空方陣は中が詰まっていない方陣。一辺の数だけでなく「列幅」を考えないといけない。
中空方陣の石の数
中空方陣の一辺と列幅から石の数を求める
一列の中空方陣
1列の中空方陣は中実方陣の最外周と同じく「(A-1)×4」個です。
●●●●●
●●●●●
●●●●●
●●●●●
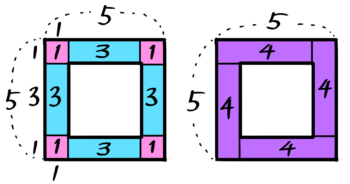
中空方陣の石は全部で(5-1)×4=16個
ここでも区切り図(井の図→渦の図)を書くと分かりやすいです。
一辺10個1列の中空方陣の石の数は?
→( (10-1)×4=9×4=36個 )
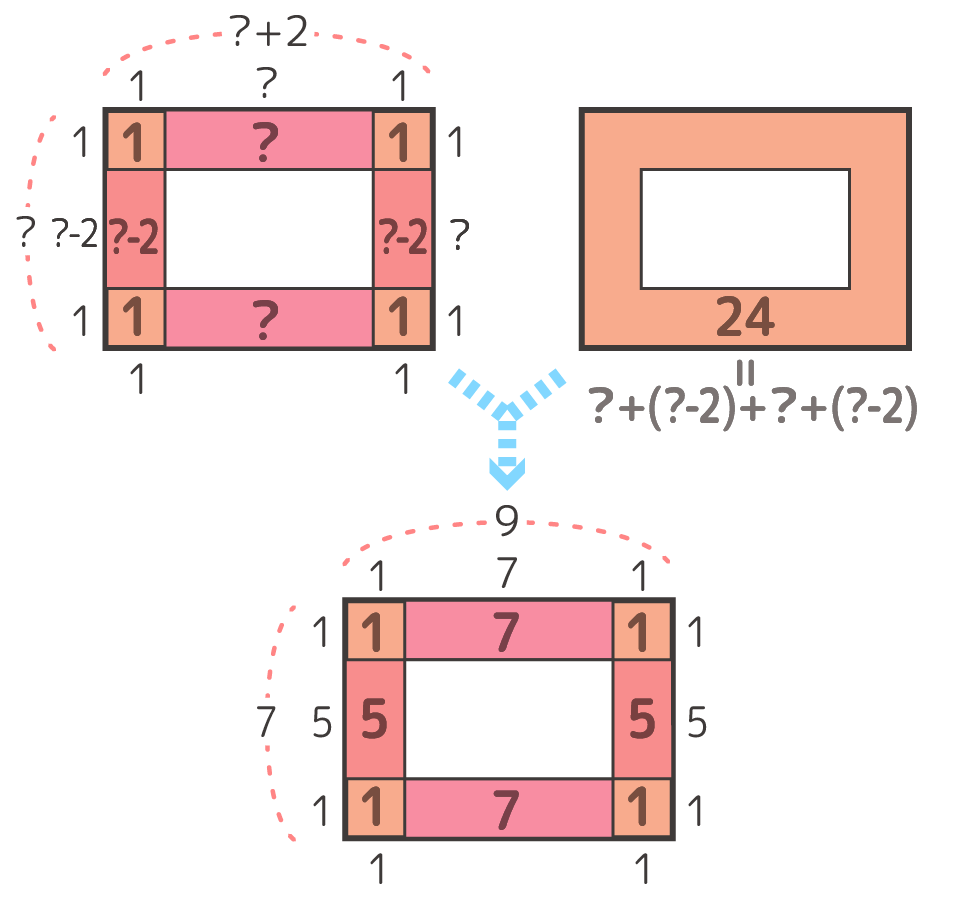
2列の中空方陣
一つの区切りは2×(A-2)の長方形になるので、石の数は{2×(A-2)}×4 個になる。
区切り絵➀(井) 区切り絵➁(渦)
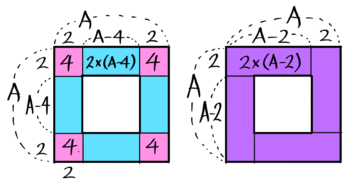
いきなり➁をかいているが
まず➀を書くことが大事
確認テストをどうぞ
一辺10個2列の中空方陣の石の数は?
→( 2×(10-2)の区切りが4つできるので )
→( 2×(10-2)×4=64個 )
3列以上の中空方陣
- 一辺A個1列の中空方陣の石の数
=( (A-1)×4 )個 - 一辺A個2列の中空方陣の石の数
=( {2×(A-2)}×4 )個 - 一辺A個3列の中空方陣の石の数
=( {3×(A-3)}×4 )個
問題を解きたい人は「中空方陣」を見て下さい
中空方陣の形を求める
石の数から中空方陣の形を求めます。
列数と石の合計から一辺を求める
列数が分かる場合は四隅が分かるので、それを手がかりにします。
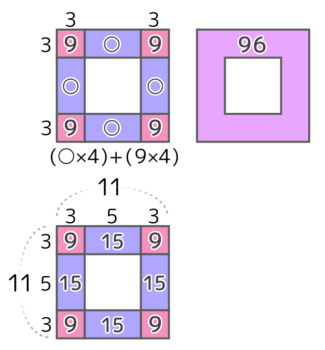
一辺と石の合計から列数を求める
一辺が分かる場合は中実方陣とした場合の個数がわかるので、実際の石との差が中の空洞になります。
この時使う公式が、一辺A個で空洞の一辺がB個の中空方陣の石の数=(A×A)-(B×B) 個 です。
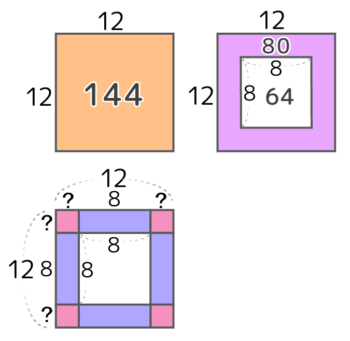
問題を解きたい人は「中空方陣」を見て下さい
長方形の中空方陣
やはり「区切り図(井の図)」を書くのが大切です
●タテA個ヨコB個,N列の中空方陣の石の数
={N×(A-N)}x2+{N×(B -N)}x2
(例)タテ12個ヨコ10個,3列の中空方陣の石の数
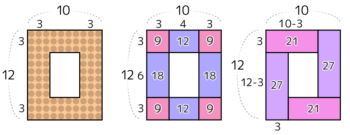
{3x(12-3)}x2+{3x(10-3)}x2=27×2+21×2=96
小まとめ
- 一辺A個1列の中空方陣の石の数
=( (A-1)×4 )個 - 一辺A個2列の中空方陣の石の数
=( {2×(A-2)}×4 )個 - 一辺A個3列の中空方陣の石の数
=( {3×(A-3)}×4 )個 - 一辺A個で空洞の一辺がB個の中空方陣の石の数
=( (A×A)-(B×B) )個
中空方陣をじっくり学習したい人は関連記事「中空方陣」を見て下さい。
三角形に石を積む
(ピラミッド算)
- N段ピラミッドの最底辺の石の個数=N個
- N段ピラミッドの石の合計
=N×(N+1)÷2 個 - N段ピラミッド(Nは奇数)の奇数段だけの石の合計
→Nは{(N+1)÷2}=M番目の奇数で
=M×M 個 - N段のピラミッドの最外周の石の個数
=(N-1)×3 個 - N段のピラミッドの最外周を
もう一周増やすのに必要な石の数
=(N+2)×3 個
ピラミッドのように
石の段が積み上がっていくイメージ
→
→
→
(一番下の石)
(石の合計)
●
●
●
1個
1個
●
●
●●
2個
1+2=3個
●
●●
●●●
3個
1+2+3=6個
最下段の石の数
一番下の段の石の数は段数と同じになっているので、N段のピラミッドの最下段の石の数はN個です。
15段のピラミッドの最下段の石は何個?
→( 15個 )
石の合計
上で見たように、1、(1+2=)3、(1+2+3=)6…と増えていくので、N段のピラミッドの石の合計は、1+2+3+…N 個になり、これは等差数列の和と同じ考え方で、N×(N+1)÷2と計算できます。
●●
●●●
●●●●
→
●●
●●●
●●●●
●●○○○
●●●○○
●●●●○
つまり、4段ピラミッドの石の合計は
4×5の長方形の半分なので、
4×(4+1)÷2 で求められる。
15段ピラミッドの石の合計は?
→( 15×(15+1)÷2=120個 )
一段おきの合計
一段おきに(奇数段だけ)石を足していくと「平方数(四角数)」になります。
一段おきの石の合計は平方数になる
●
●
1段
1個
(1×1)
●
●●
●●●
3段
1+3=
4個
(2×2)
●●
●●●
●●●●
●●●●●
5段
1+3+5=
9個
(3×3)
●●
●●●
●●●●
●●●●●
●●●●●●
●●●●●●●
7段
1+3+5+7=
16個
(4×4)
例えば5段ピラミッドの場合「5」は奇数としては(5+1)÷2=「3」番目なので、奇数段の石●の数は3×3=9個になります。
奇数段は黒い石、偶数段は白い石で15段のピラミッドを作る時、黒い石は何個か?
→( 15段ピラミッドは奇数では(15+1)÷2=8番目のピラミッドなので、その奇数段(黒い石)の合計は8×8=64個 )
さっきの15段ピラミッドの白い石の個数は?
→( 15段ピラミッドの全部の石の合計は15×(15+1)÷2=120個で、黒い石が64個あるから、白い石は120-64=56個 )
詳しい説明が読みたい人は「三角形に並べるピラミッド算」を見て下さい。
最外周の石の数
これは方陣と同じような「区切り」を考えれば良いですね。
(例)5段ピラミッドの最外周の石
●●
●●●
●●●●
●●●●●
→
●●
●●●
●●●●
●●●●●
●●
●●●
●●●●
●●●●●
一つづつ組み合わせると
5-1=4個の石を含む「区切り」が3つできるので
最外周の石は4×3=12
N段のピラミッドの最外周の石は (N-1)×3 と分かります。
15段ピラミッドの最外周の石の個数は?
→( (15-1)×3=42個 )
詳しい説明が読みたい人は「三角形に並べるピラミッド算」を見て下さい。
石を多角形に並べる
●特徴:中心に「へそ石」がある
●一辺A個のN角形に並べた石の合計
→1個のへそ石と一辺(A-1)個のピラミッドがN個
=1+{(A-1)×A÷2}×N
(例)一辺4個の五角形に並べた場合
→1+{(4-1)×4÷2}×5=31個
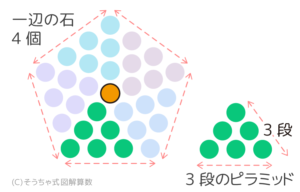
● 〃 最外周の石の合計
→(A-1)個の石を含む区切りがN個
= (A-1)×N
(例)一辺4個の五角形→(4-1)×5=15個
多角形並べの特徴
「多角形並べ」は中心に必ず1個の石(へそ石)があります。

上で見た「方陣」や「ピラミッド」には中心が無いこともあります。
多角形並べの石の数
中心となる石(へそ)以外の石をピラミッドに分解します。
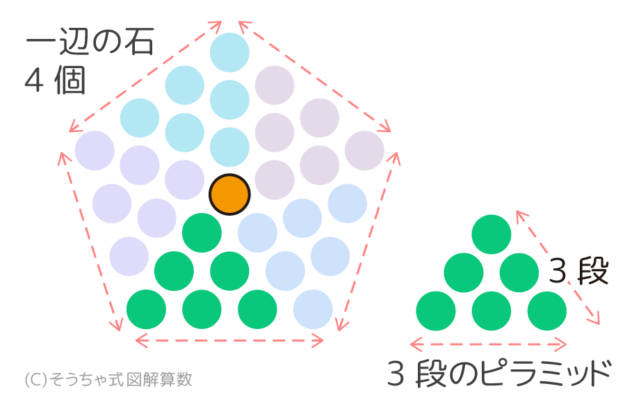 4-1=3段の「ピラミッド」が5個と
4-1=3段の「ピラミッド」が5個と「へそ石」に分割できる。
このピラミッドは多角形の辺の長さよりも1個少ない段になります。一辺4個の五角形の場合、ピラミッドは4-1=3段になります。
そして、3段のピラミッドには3×(3+1)÷2=6個の石があって、これが5セット30個あります。
さらに中心の「へそ」1個を加えた31個が石の合計になります。
一辺10個の六角形に並べた石の数の合計は?
→へそ石1個と( 10-1=9段のピラミッド6個に分割できる。)
→ピラミッド1つに含まれる石は( 9×(9+1)÷2=45個 )なので
→合計は( (45×6)+1=271個 )
多角形並べの最外周の石
方陣算と同じように「最外周の区切」を考える。
((方陣、五角形並べ、六角形並べの「実体図」と「区切り絵」))
一辺6の五角形の場合は最外周に5個の石を含む区切りが5個できるので(6-1)×5=25個になります。
一辺10個の正七角形に並べた石の最外周の石の数は?
→最外周には( (10-1)=9個 )の石を含む区切りが( 7個 )できる
→最外周の石の数は( 9×7=63個 )
オススメ教材
 爽茶
爽茶●方陣算だけを解きたい場合は「方陣算(基本)(応用)」(サイパー算数)
●その他の単元を合わせて予習復習をしたい場合、「算数の基本問題4年」(日能研)
●小6受験生には「算数ベストチェック」(日能研)
分かりやすい!と評判のスタディサプリなら中学受験用の授業動画が沢山ありますよ。今なら14日間無料。興味がある人は「先取りや予習・復習に! スタディサプリ そうちゃ式のオススメ利用法」へ
2023年度生徒さん募集
2023年度の生徒さんの募集を開始しました(対面授業の一次募集)
東武野田線・伊勢崎線沿線にお住まいの新5年生で予習シリーズをベースにされている方が対象です。
詳しくはコチラのページを御覧下さい
新4年生の方を対象に学習相談/授業を実施します(サピックス新越谷校・南浦和校・大宮校の方が対象。締め切り2/1)。応募はコチラから
中学受験でお悩みの方へ
 そうちゃ
そうちゃ受験に関する悩みはつきませんね。「中学受験と高校受験とどちらがいいの?」「塾の選び方は?」「途中から塾に入っても大丈夫?」「塾の成績・クラスが下がった…」「志望校の過去問が出来ない…」など
様々なお悩みへのアドバイスを記事にまとめたので参考にして下さい。
自分だけで悩んでいると煮詰まってしまい、事態を改善できないかもしないこともあるでしょう…
そんな時は、講師経験20年の「そうちゃ」に相談してみませんか?対面/オンラインの授業/学習相談を受け付けているので、ご利用下さい。
この記事があなたの役に立てたなら嬉しいです!